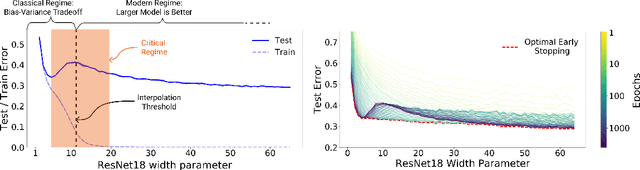
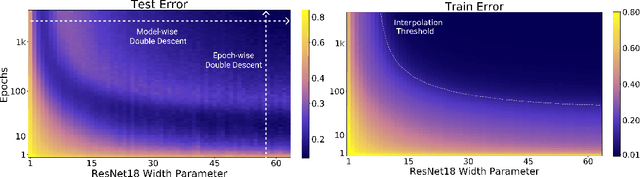
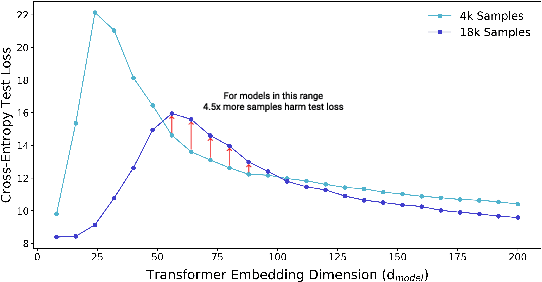
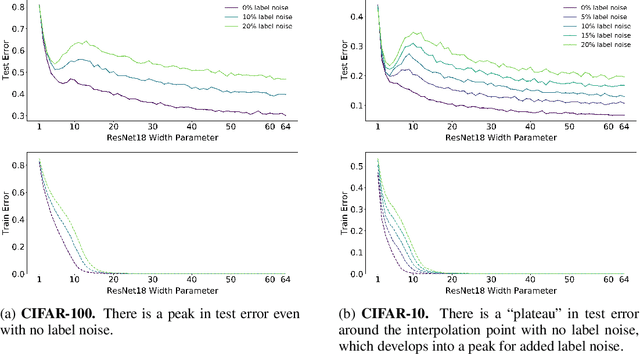
Deep Double Descent: Where Bigger Models and More Data Hurt

We show that a variety of modern deep learning tasks exhibit a "double-descent" phenomenon where, as we increase model size, performance first gets worse and then gets better. Moreover, we show that double descent occurs not just as a function of model size, but also as a function of the number of training epochs. We unify the above phenomena by defining a new complexity measure we call the effective model complexity and conjecture a generalized double descent with respect to this measure. Furthermore, our notion of model complexity allows us to identify certain regimes where increasing (even quadrupling) the number of train samples actually hurts test performance.

SGD on Neural Networks Learns Functions of Increasing Complexity

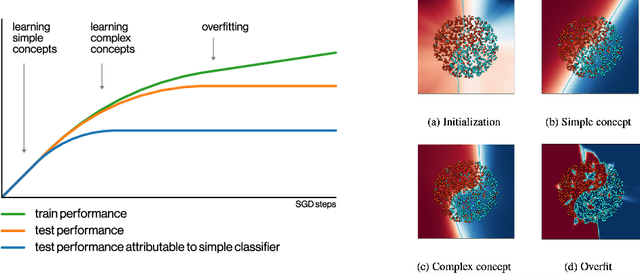
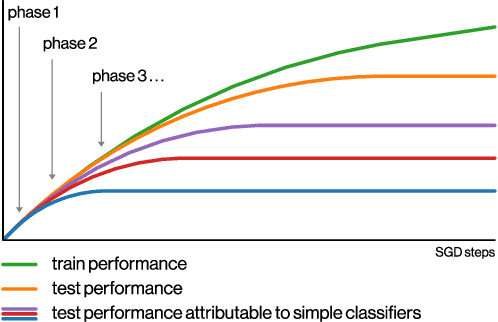
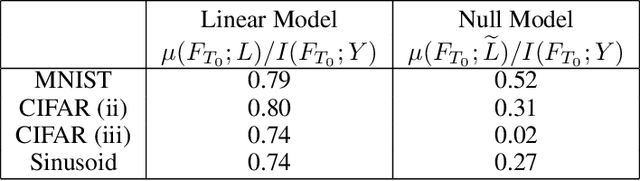
We perform an experimental study of the dynamics of Stochastic Gradient Descent (SGD) in learning deep neural networks for several real and synthetic classification tasks. We show that in the initial epochs, almost all of the performance improvement of the classifier obtained by SGD can be explained by a linear classifier. More generally, we give evidence for the hypothesis that, as iterations progress, SGD learns functions of increasing complexity. This hypothesis can be helpful in explaining why SGD-learned classifiers tend to generalize well even in the over-parameterized regime. We also show that the linear classifier learned in the initial stages is "retained" throughout the execution even if training is continued to the point of zero training error, and complement this with a theoretical result in a simplified model. Key to our work is a new measure of how well one classifier explains the performance of another, based on conditional mutual information.