Beyond Human Data: Scaling Self-Training for Problem-Solving with Language Models

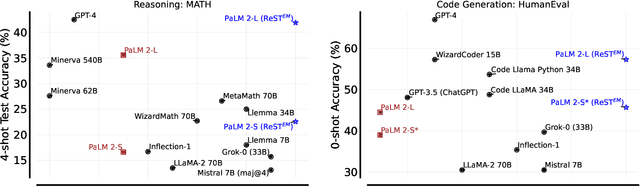
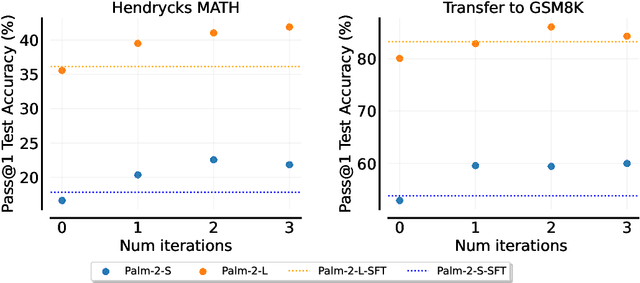
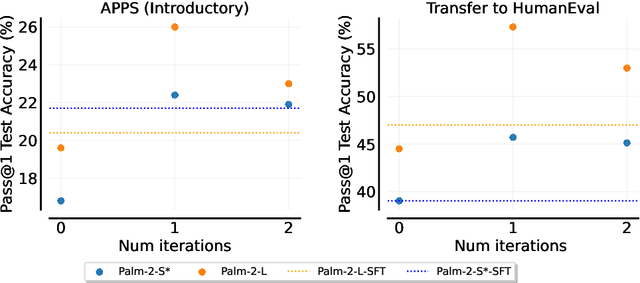
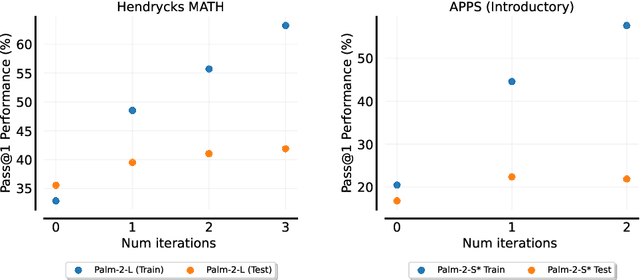
Fine-tuning language models~(LMs) on human-generated data remains a prevalent practice. However, the performance of such models is often limited by the quantity and diversity of high-quality human data. In this paper, we explore whether we can go beyond human data on tasks where we have access to scalar feedback, for example, on math problems where one can verify correctness. To do so, we investigate a simple self-training method based on expectation-maximization, which we call ReST$^{EM}$, where we (1) generate samples from the model and filter them using binary feedback, (2) fine-tune the model on these samples, and (3) repeat this process a few times. Testing on advanced MATH reasoning and APPS coding benchmarks using PaLM-2 models, we find that ReST$^{EM}$ scales favorably with model size and significantly surpasses fine-tuning only on human data. Overall, our findings suggest self-training with feedback can substantially reduce dependence on human-generated data.

Gemini: A Family of Highly Capable Multimodal Models

This report introduces a new family of multimodal models, Gemini, that exhibit remarkable capabilities across image, audio, video, and text understanding. The Gemini family consists of Ultra, Pro, and Nano sizes, suitable for applications ranging from complex reasoning tasks to on-device memory-constrained use-cases. Evaluation on a broad range of benchmarks shows that our most-capable Gemini Ultra model advances the state of the art in 30 of 32 of these benchmarks - notably being the first model to achieve human-expert performance on the well-studied exam benchmark MMLU, and improving the state of the art in every one of the 20 multimodal benchmarks we examined. We believe that the new capabilities of Gemini models in cross-modal reasoning and language understanding will enable a wide variety of use cases and we discuss our approach toward deploying them responsibly to users.

On Privileged and Convergent Bases in Neural Network Representations

In this study, we investigate whether the representations learned by neural networks possess a privileged and convergent basis. Specifically, we examine the significance of feature directions represented by individual neurons. First, we establish that arbitrary rotations of neural representations cannot be inverted (unlike linear networks), indicating that they do not exhibit complete rotational invariance. Subsequently, we explore the possibility of multiple bases achieving identical performance. To do this, we compare the bases of networks trained with the same parameters but with varying random initializations. Our study reveals two findings: (1) Even in wide networks such as WideResNets, neural networks do not converge to a unique basis; (2) Basis correlation increases significantly when a few early layers of the network are frozen identically. Furthermore, we analyze Linear Mode Connectivity, which has been studied as a measure of basis correlation. Our findings give evidence that while Linear Mode Connectivity improves with increased network width, this improvement is not due to an increase in basis correlation.

The unreasonable effectiveness of few-shot learning for machine translation

We demonstrate the potential of few-shot translation systems, trained with unpaired language data, for both high and low-resource language pairs. We show that with only 5 examples of high-quality translation data shown at inference, a transformer decoder-only model trained solely with self-supervised learning, is able to match specialized supervised state-of-the-art models as well as more general commercial translation systems. In particular, we outperform the best performing system on the WMT'21 English - Chinese news translation task by only using five examples of English - Chinese parallel data at inference. Moreover, our approach in building these models does not necessitate joint multilingual training or back-translation, is conceptually simple and shows the potential to extend to the multilingual setting. Furthermore, the resulting models are two orders of magnitude smaller than state-of-the-art language models. We then analyze the factors which impact the performance of few-shot translation systems, and highlight that the quality of the few-shot demonstrations heavily determines the quality of the translations generated by our models. Finally, we show that the few-shot paradigm also provides a way to control certain attributes of the translation -- we show that we are able to control for regional varieties and formality using only a five examples at inference, paving the way towards controllable machine translation systems.

Limitations of the NTK for Understanding Generalization in Deep Learning

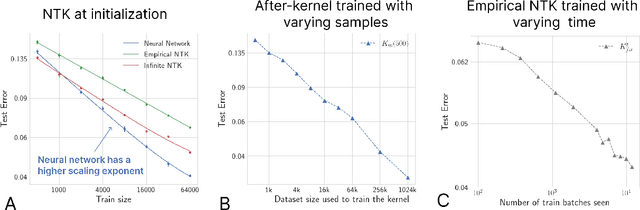
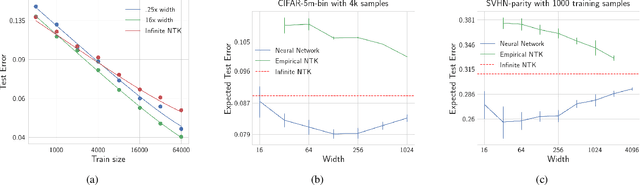
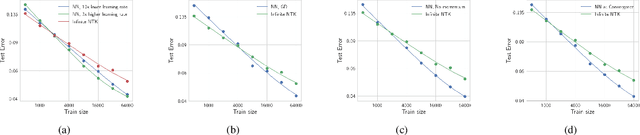
The ``Neural Tangent Kernel'' (NTK) (Jacot et al 2018), and its empirical variants have been proposed as a proxy to capture certain behaviors of real neural networks. In this work, we study NTKs through the lens of scaling laws, and demonstrate that they fall short of explaining important aspects of neural network generalization. In particular, we demonstrate realistic settings where finite-width neural networks have significantly better data scaling exponents as compared to their corresponding empirical and infinite NTKs at initialization. This reveals a more fundamental difference between the real networks and NTKs, beyond just a few percentage points of test accuracy. Further, we show that even if the empirical NTK is allowed to be pre-trained on a constant number of samples, the kernel scaling does not catch up to the neural network scaling. Finally, we show that the empirical NTK continues to evolve throughout most of the training, in contrast with prior work which suggests that it stabilizes after a few epochs of training. Altogether, our work establishes concrete limitations of the NTK approach in understanding generalization of real networks on natural datasets.

Data Scaling Laws in NMT: The Effect of Noise and Architecture

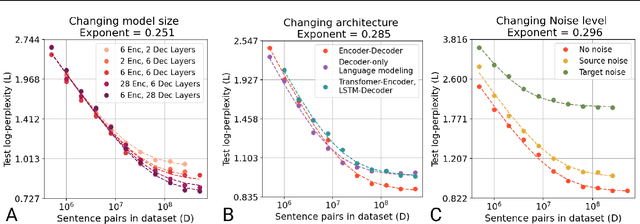
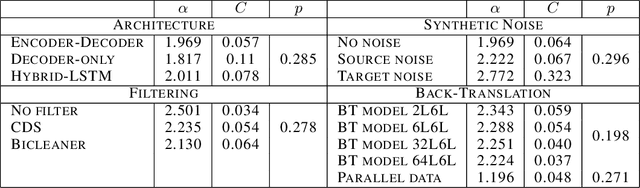
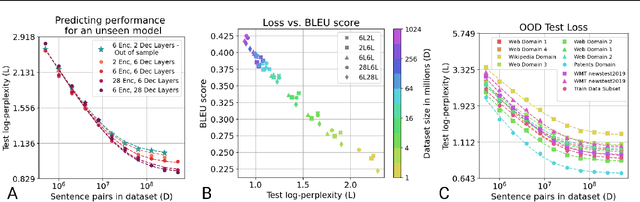
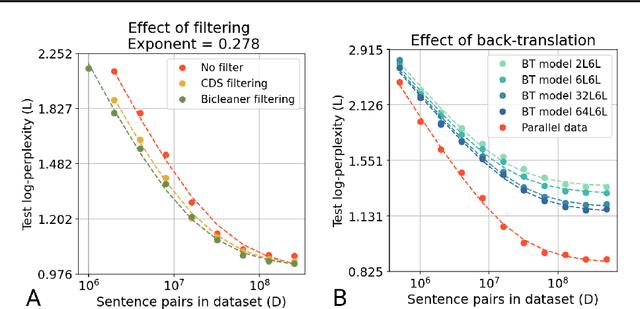
In this work, we study the effect of varying the architecture and training data quality on the data scaling properties of Neural Machine Translation (NMT). First, we establish that the test loss of encoder-decoder transformer models scales as a power law in the number of training samples, with a dependence on the model size. Then, we systematically vary aspects of the training setup to understand how they impact the data scaling laws. In particular, we change the following (1) Architecture and task setup: We compare to a transformer-LSTM hybrid, and a decoder-only transformer with a language modeling loss (2) Noise level in the training distribution: We experiment with filtering, and adding iid synthetic noise. In all the above cases, we find that the data scaling exponents are minimally impacted, suggesting that marginally worse architectures or training data can be compensated for by adding more data. Lastly, we find that using back-translated data instead of parallel data, can significantly degrade the scaling exponent.

Revisiting Model Stitching to Compare Neural Representations

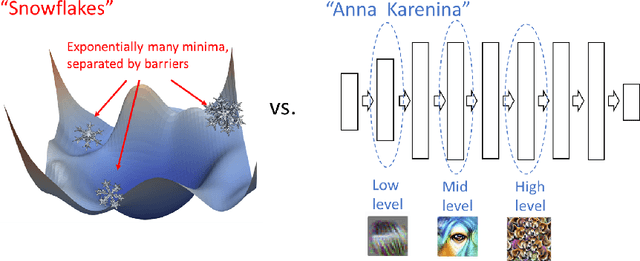
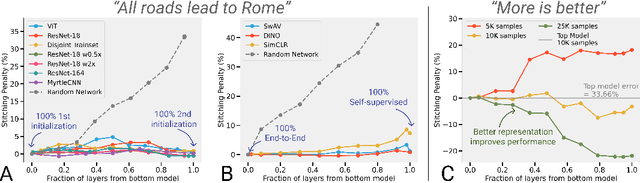
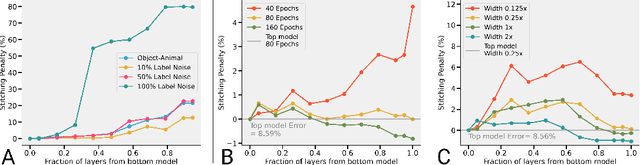
We revisit and extend model stitching (Lenc & Vedaldi 2015) as a methodology to study the internal representations of neural networks. Given two trained and frozen models $A$ and $B$, we consider a "stitched model'' formed by connecting the bottom-layers of $A$ to the top-layers of $B$, with a simple trainable layer between them. We argue that model stitching is a powerful and perhaps under-appreciated tool, which reveals aspects of representations that measures such as centered kernel alignment (CKA) cannot. Through extensive experiments, we use model stitching to obtain quantitative verifications for intuitive statements such as "good networks learn similar representations'', by demonstrating that good networks of the same architecture, but trained in very different ways (e.g.: supervised vs. self-supervised learning), can be stitched to each other without drop in performance. We also give evidence for the intuition that "more is better'' by showing that representations learnt with (1) more data, (2) bigger width, or (3) more training time can be "plugged in'' to weaker models to improve performance. Finally, our experiments reveal a new structural property of SGD which we call "stitching connectivity'', akin to mode-connectivity: typical minima reached by SGD can all be stitched to each other with minimal change in accuracy.

Improving the Reconstruction of Disentangled Representation Learners via Multi-Stage Modelling

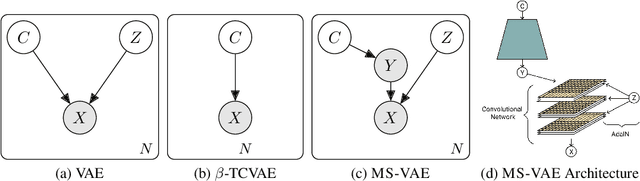
Current autoencoder-based disentangled representation learning methods achieve disentanglement by penalizing the (aggregate) posterior to encourage statistical independence of the latent factors. This approach introduces a trade-off between disentangled representation learning and reconstruction quality since the model does not have enough capacity to learn correlated latent variables that capture detail information present in most image data. To overcome this trade-off, we present a novel multi-stage modelling approach where the disentangled factors are first learned using a preexisting disentangled representation learning method (such as $\beta$-TCVAE); then, the low-quality reconstruction is improved with another deep generative model that is trained to model the missing correlated latent variables, adding detail information while maintaining conditioning on the previously learned disentangled factors. Taken together, our multi-stage modelling approach results in a single, coherent probabilistic model that is theoretically justified by the principal of D-separation and can be realized with a variety of model classes including likelihood-based models such as variational autoencoders, implicit models such as generative adversarial networks, and tractable models like normalizing flows or mixtures of Gaussians. We demonstrate that our multi-stage model has much higher reconstruction quality than current state-of-the-art methods with equivalent disentanglement performance across multiple standard benchmarks.

For self-supervised learning, Rationality implies generalization, provably

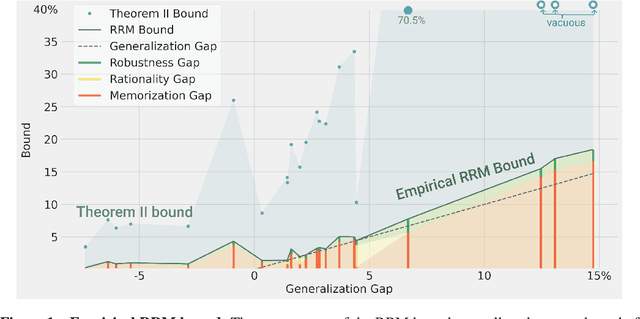
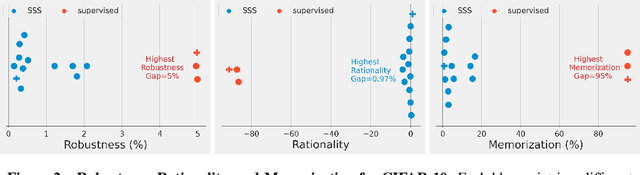
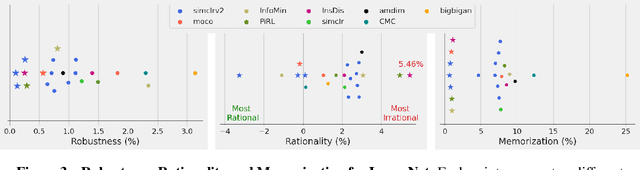
We prove a new upper bound on the generalization gap of classifiers that are obtained by first using self-supervision to learn a representation $r$ of the training data, and then fitting a simple (e.g., linear) classifier $g$ to the labels. Specifically, we show that (under the assumptions described below) the generalization gap of such classifiers tends to zero if $\mathsf{C}(g) \ll n$, where $\mathsf{C}(g)$ is an appropriately-defined measure of the simple classifier $g$'s complexity, and $n$ is the number of training samples. We stress that our bound is independent of the complexity of the representation $r$. We do not make any structural or conditional-independence assumptions on the representation-learning task, which can use the same training dataset that is later used for classification. Rather, we assume that the training procedure satisfies certain natural noise-robustness (adding small amount of label noise causes small degradation in performance) and rationality (getting the wrong label is not better than getting no label at all) conditions that widely hold across many standard architectures. We show that our bound is non-vacuous for many popular representation-learning based classifiers on CIFAR-10 and ImageNet, including SimCLR, AMDIM and MoCo.

Distributional Generalization: A New Kind of Generalization

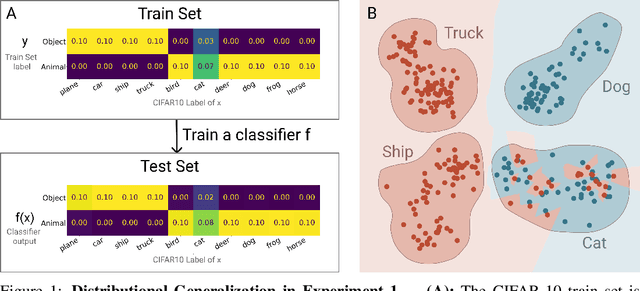
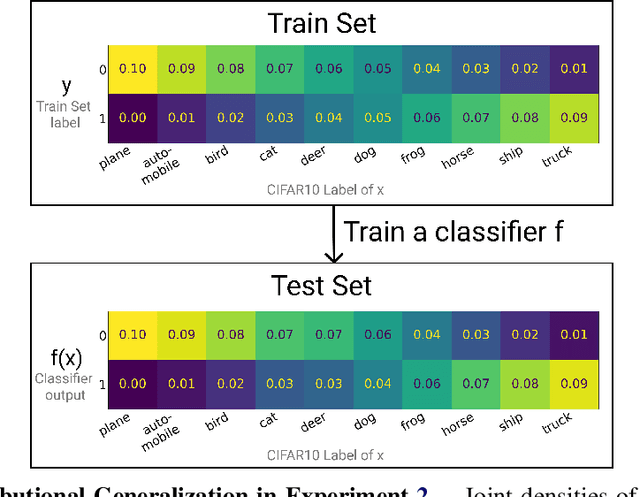
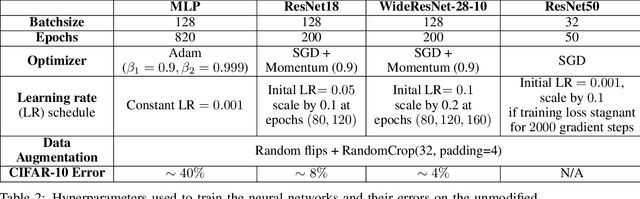
We introduce a new notion of generalization-- Distributional Generalization-- which roughly states that outputs of a classifier at train and test time are close *as distributions*, as opposed to close in just their average error. For example, if we mislabel 30% of dogs as cats in the train set of CIFAR-10, then a ResNet trained to interpolation will in fact mislabel roughly 30% of dogs as cats on the *test set* as well, while leaving other classes unaffected. This behavior is not captured by classical generalization, which would only consider the average error and not the distribution of errors over the input domain. This example is a specific instance of our much more general conjectures which apply even on distributions where the Bayes risk is zero. Our conjectures characterize the form of distributional generalization that can be expected, in terms of problem parameters (model architecture, training procedure, number of samples, data distribution). We verify the quantitative predictions of these conjectures across a variety of domains in machine learning, including neural networks, kernel machines, and decision trees. These empirical observations are independently interesting, and form a more fine-grained characterization of interpolating classifiers beyond just their test error.