Revisiting Model Stitching to Compare Neural Representations
Paper and Code
Jun 14, 2021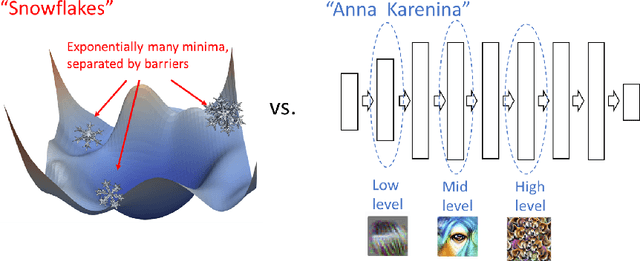

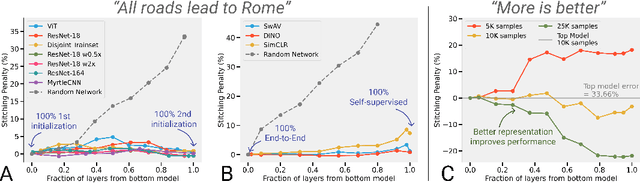
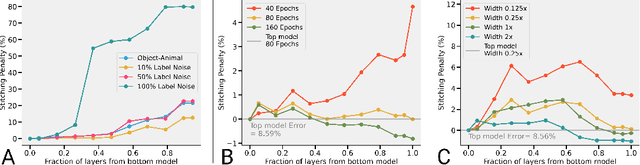
We revisit and extend model stitching (Lenc & Vedaldi 2015) as a methodology to study the internal representations of neural networks. Given two trained and frozen models $A$ and $B$, we consider a "stitched model'' formed by connecting the bottom-layers of $A$ to the top-layers of $B$, with a simple trainable layer between them. We argue that model stitching is a powerful and perhaps under-appreciated tool, which reveals aspects of representations that measures such as centered kernel alignment (CKA) cannot. Through extensive experiments, we use model stitching to obtain quantitative verifications for intuitive statements such as "good networks learn similar representations'', by demonstrating that good networks of the same architecture, but trained in very different ways (e.g.: supervised vs. self-supervised learning), can be stitched to each other without drop in performance. We also give evidence for the intuition that "more is better'' by showing that representations learnt with (1) more data, (2) bigger width, or (3) more training time can be "plugged in'' to weaker models to improve performance. Finally, our experiments reveal a new structural property of SGD which we call "stitching connectivity'', akin to mode-connectivity: typical minima reached by SGD can all be stitched to each other with minimal change in accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge