Distributional Generalization: A New Kind of Generalization

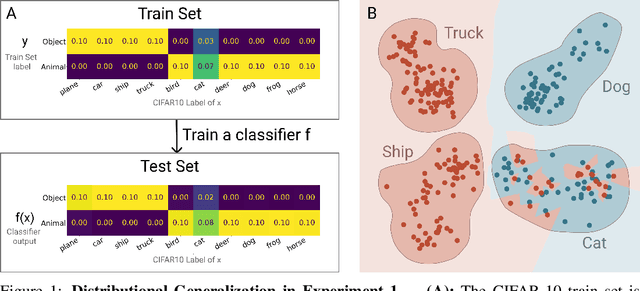
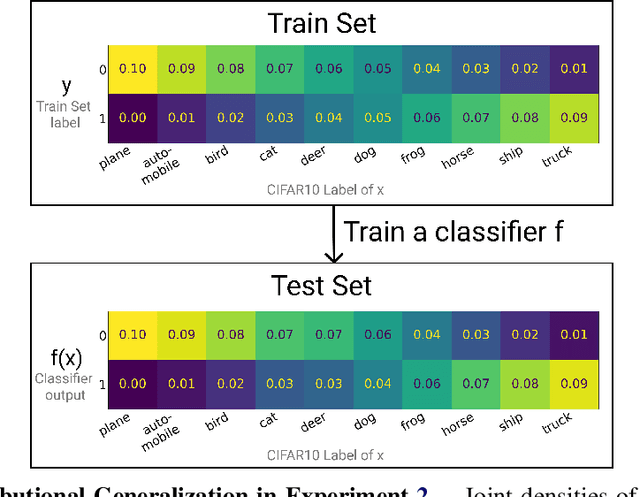
We introduce a new notion of generalization-- Distributional Generalization-- which roughly states that outputs of a classifier at train and test time are close *as distributions*, as opposed to close in just their average error. For example, if we mislabel 30% of dogs as cats in the train set of CIFAR-10, then a ResNet trained to interpolation will in fact mislabel roughly 30% of dogs as cats on the *test set* as well, while leaving other classes unaffected. This behavior is not captured by classical generalization, which would only consider the average error and not the distribution of errors over the input domain. This example is a specific instance of our much more general conjectures which apply even on distributions where the Bayes risk is zero. Our conjectures characterize the form of distributional generalization that can be expected, in terms of problem parameters (model architecture, training procedure, number of samples, data distribution). We verify the quantitative predictions of these conjectures across a variety of domains in machine learning, including neural networks, kernel machines, and decision trees. These empirical observations are independently interesting, and form a more fine-grained characterization of interpolating classifiers beyond just their test error.