Instance Specific Approximations for Submodular Maximization
Paper and Code
Feb 23, 2021
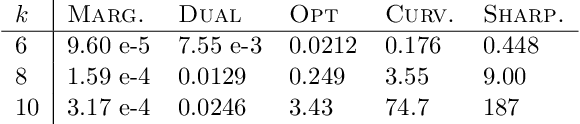

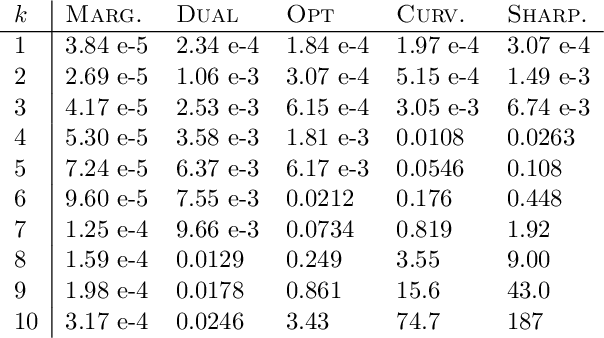
For many optimization problems in machine learning, finding an optimal solution is computationally intractable and we seek algorithms that perform well in practice. Since computational intractability often results from pathological instances, we look for methods to benchmark the performance of algorithms against optimal solutions on real-world instances. The main challenge is that an optimal solution cannot be efficiently computed for intractable problems, and we therefore often do not know how far a solution is from being optimal. A major question is therefore how to measure the performance of an algorithm in comparison to an optimal solution on instances we encounter in practice. In this paper, we address this question in the context of submodular optimization problems. For the canonical problem of submodular maximization under a cardinality constraint, it is intractable to compute a solution that is better than a $1-1/e \approx 0.63$ fraction of the optimum. Algorithms like the celebrated greedy algorithm are guaranteed to achieve this $1-1/e$ bound on any instance and are used in practice. Our main contribution is not a new algorithm for submodular maximization but an analytical method that measures how close an algorithm for submodular maximization is to optimal on a given problem instance. We use this method to show that on a wide variety of real-world datasets and objectives, the approximation of the solution found by greedy goes well beyond $1-1/e$ and is often at least 0.95. We develop this method using a novel technique that lower bounds the objective of a dual minimization problem to obtain an upper bound on the value of an optimal solution to the primal maximization problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge