The FAST Algorithm for Submodular Maximization
Paper and Code
Jul 14, 2019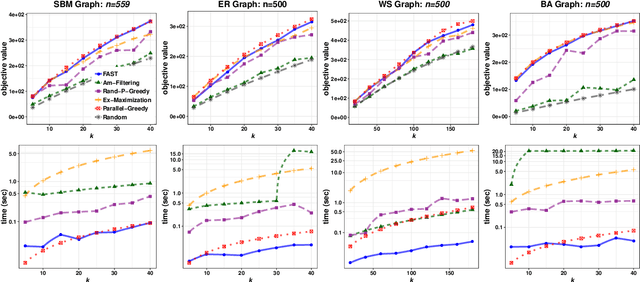
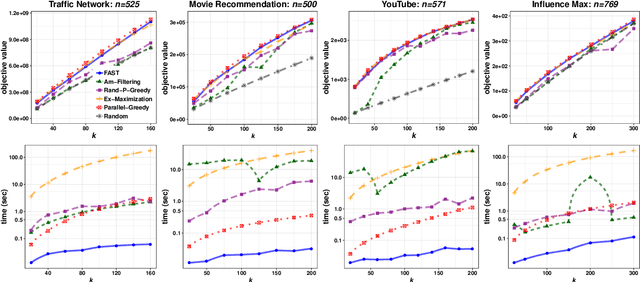
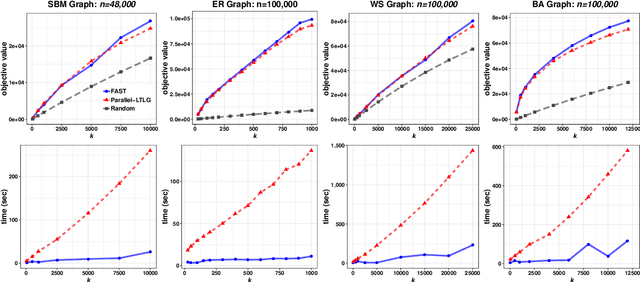
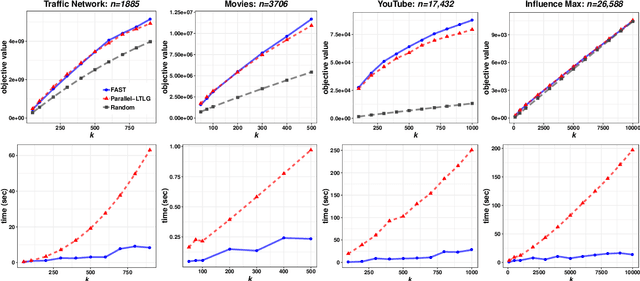
In this paper we describe a new algorithm called Fast Adaptive Sequencing Technique (FAST) for maximizing a monotone submodular function under a cardinality constraint $k$ whose approximation ratio is arbitrarily close to $1-1/e$, is $O(\log(n) \log^2(\log k))$ adaptive, and uses a total of $O(n \log\log(k))$ queries. Recent algorithms have comparable guarantees in terms of asymptotic worst case analysis, but their actual number of rounds and query complexity depend on very large constants and polynomials in terms of precision and confidence, making them impractical for large data sets. Our main contribution is a design that is extremely efficient both in terms of its non-asymptotic worst case query complexity and number of rounds, and in terms of its practical runtime. We show that this algorithm outperforms any algorithm for submodular maximization we are aware of, including hyper-optimized parallel versions of state-of-the-art serial algorithms, by running experiments on large data sets. These experiments show FAST is orders of magnitude faster than the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge