Umar Syed
Learning from Synthetic Data: Limitations of ERM
Jan 21, 2026Abstract:The prevalence and low cost of LLMs have led to a rise of synthetic content. From review sites to court documents, ``natural'' content has been contaminated by data points that appear similar to natural data, but are in fact LLM-generated. In this work we revisit fundamental learning theory questions in this, now ubiquitous, setting. We model this scenario as a sequence of learning tasks where the input is a mix of natural and synthetic data, and the learning algorithms are oblivious to the origin of any individual example. We study the possibilities and limitations of ERM in this setting. For the problem of estimating the mean of an arbitrary $d$-dimensional distribution, we find that while ERM converges to the true mean, it is outperformed by an algorithm that assigns non-uniform weights to examples from different generations of data. For the PAC learning setting, the disparity is even more stark. We find that ERM does not always converge to the true concept, echoing the model collapse literature. However, we show there are algorithms capable of learning the correct hypothesis for arbitrary VC classes and arbitrary amounts of contamination.
Clustering and Median Aggregation Improve Differentially Private Inference
Jun 05, 2025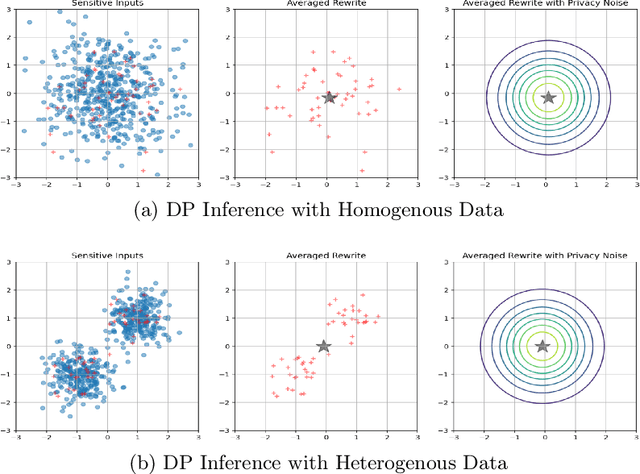

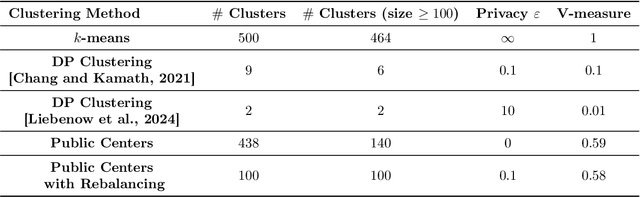
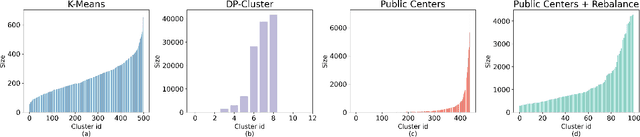
Abstract:Differentially private (DP) language model inference is an approach for generating private synthetic text. A sensitive input example is used to prompt an off-the-shelf large language model (LLM) to produce a similar example. Multiple examples can be aggregated together to formally satisfy the DP guarantee. Prior work creates inference batches by sampling sensitive inputs uniformly at random. We show that uniform sampling degrades the quality of privately generated text, especially when the sensitive examples concern heterogeneous topics. We remedy this problem by clustering the input data before selecting inference batches. Next, we observe that clustering also leads to more similar next-token predictions across inferences. We use this insight to introduce a new algorithm that aggregates next token statistics by privately computing medians instead of averages. This approach leverages the fact that the median has decreased local sensitivity when next token predictions are similar, allowing us to state a data-dependent and ex-post DP guarantee about the privacy properties of this algorithm. Finally, we demonstrate improvements in terms of representativeness metrics (e.g., MAUVE) as well as downstream task performance. We show that our method produces high-quality synthetic data at significantly lower privacy cost than a previous state-of-the-art method.
Near-optimal algorithms for private estimation and sequential testing of collision probability
Apr 18, 2025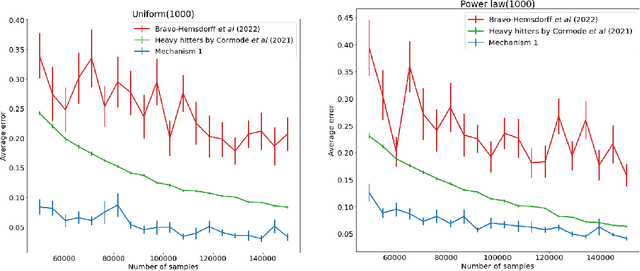
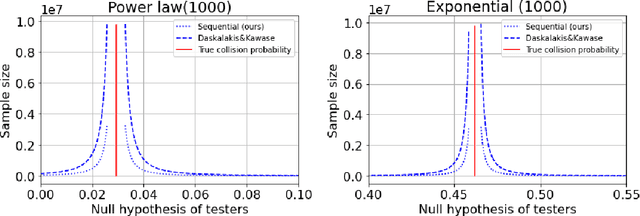
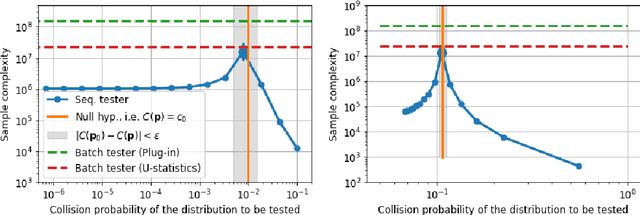
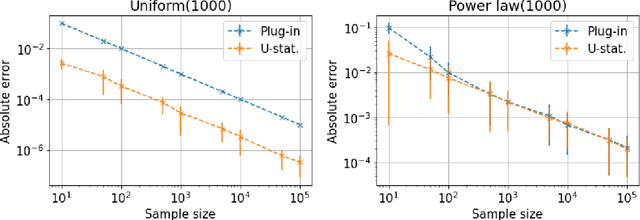
Abstract:We present new algorithms for estimating and testing \emph{collision probability}, a fundamental measure of the spread of a discrete distribution that is widely used in many scientific fields. We describe an algorithm that satisfies $(\alpha, \beta)$-local differential privacy and estimates collision probability with error at most $\epsilon$ using $\tilde{O}\left(\frac{\log(1/\beta)}{\alpha^2 \epsilon^2}\right)$ samples for $\alpha \le 1$, which improves over previous work by a factor of $\frac{1}{\alpha^2}$. We also present a sequential testing algorithm for collision probability, which can distinguish between collision probability values that are separated by $\epsilon$ using $\tilde{O}(\frac{1}{\epsilon^2})$ samples, even when $\epsilon$ is unknown. Our algorithms have nearly the optimal sample complexity, and in experiments we show that they require significantly fewer samples than previous methods.
Escaping Collapse: The Strength of Weak Data for Large Language Model Training
Feb 13, 2025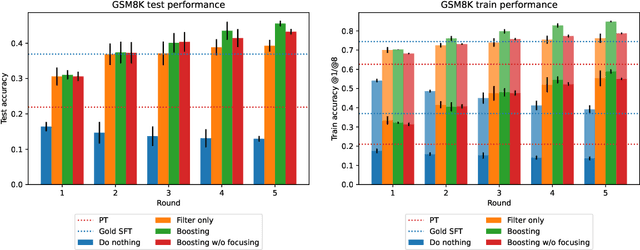
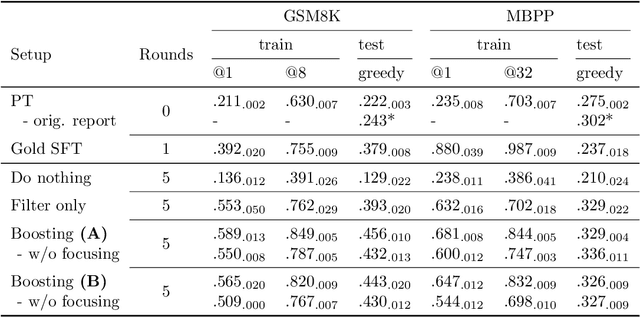
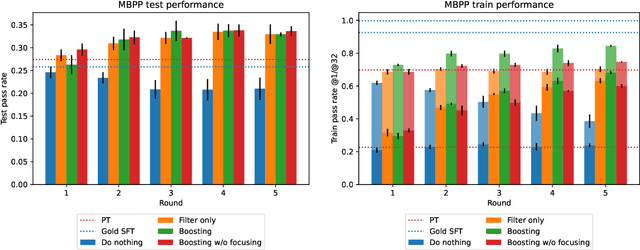
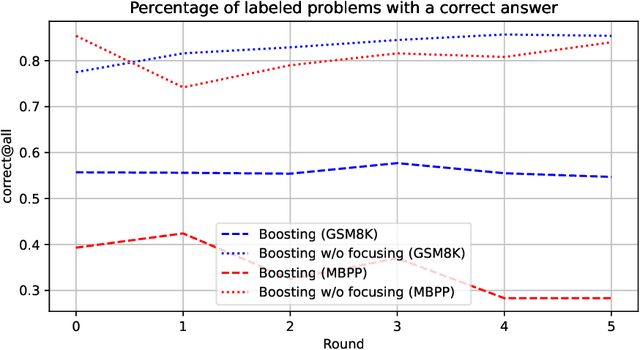
Abstract:Synthetically-generated data plays an increasingly larger role in training large language models. However, while synthetic data has been found to be useful, studies have also shown that without proper curation it can cause LLM performance to plateau, or even "collapse", after many training iterations. In this paper, we formalize this question and develop a theoretical framework to investigate how much curation is needed in order to ensure that LLM performance continually improves. We find that the requirements are nearly minimal. We describe a training procedure that converges to an optimal LLM even if almost all of the non-synthetic training data is of poor quality. Our analysis is inspired by boosting, a classic machine learning technique that leverages a very weak learning algorithm to produce an arbitrarily good classifier. Our training procedure subsumes many recently proposed methods for training LLMs on synthetic data, and thus our analysis sheds light on why they are successful, and also suggests opportunities for future improvement. We present experiments that validate our theory, and show that dynamically focusing labeling resources on the most challenging examples -- in much the same way that boosting focuses the efforts of the weak learner -- leads to improved performance.
Private prediction for large-scale synthetic text generation
Jul 16, 2024Abstract:We present an approach for generating differentially private synthetic text using large language models (LLMs), via private prediction. In the private prediction framework, we only require the output synthetic data to satisfy differential privacy guarantees. This is in contrast to approaches that train a generative model on potentially sensitive user-supplied source data and seek to ensure the model itself is safe to release. We prompt a pretrained LLM with source data, but ensure that next-token predictions are made with differential privacy guarantees. Previous work in this paradigm reported generating a small number of examples (<10) at reasonable privacy levels, an amount of data that is useful only for downstream in-context learning or prompting. In contrast, we make changes that allow us to generate thousands of high-quality synthetic data points, greatly expanding the set of potential applications. Our improvements come from an improved privacy analysis and a better private selection mechanism, which makes use of the equivalence between the softmax layer for sampling tokens in LLMs and the exponential mechanism. Furthermore, we introduce a novel use of public predictions via the sparse vector technique, in which we do not pay privacy costs for tokens that are predictable without sensitive data; we find this to be particularly effective for structured data.
Harnessing large-language models to generate private synthetic text
Jun 02, 2023
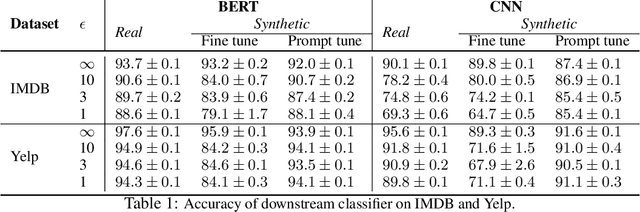


Abstract:Differentially private (DP) training methods like DP-SGD can protect sensitive training data by ensuring that ML models will not reveal private information. An alternative approach, which this paper studies, is to use a sensitive dataset to generate a new synthetic dataset which is differentially private with respect to the original data. Doing so has several advantages: synthetic data can be reused for other tasks (including for hyper parameter tuning), retained indefinitely, or shared with third parties without sacrificing privacy. However, obtaining DP data is much harder than introducing DP during training. To make it feasible for text, recent work has utilized public data by starting with a pre-trained generative language model and privately finetuning it on sensitive data. This model can be used to sample a DP synthetic dataset. While this strategy seems straightforward, executing it has proven problematic. Previous approaches either show significant performance loss, or have, as we show, critical design flaws. In this paper we demonstrate that a proper training objective along with tuning fewer parameters results in excellent DP synthetic data quality. Our approach is competitive with direct DP-training of downstream classifiers in terms of performance on downstream tasks. We also demonstrate that our DP synthetic data is not only useful for downstream classifier training, but also to tune those same models.
Private and Communication-Efficient Algorithms for Entropy Estimation
May 12, 2023Abstract:Modern statistical estimation is often performed in a distributed setting where each sample belongs to a single user who shares their data with a central server. Users are typically concerned with preserving the privacy of their samples, and also with minimizing the amount of data they must transmit to the server. We give improved private and communication-efficient algorithms for estimating several popular measures of the entropy of a distribution. All of our algorithms have constant communication cost and satisfy local differential privacy. For a joint distribution over many variables whose conditional independence is given by a tree, we describe algorithms for estimating Shannon entropy that require a number of samples that is linear in the number of variables, compared to the quadratic sample complexity of prior work. We also describe an algorithm for estimating Gini entropy whose sample complexity has no dependence on the support size of the distribution and can be implemented using a single round of concurrent communication between the users and the server. In contrast, the previously best-known algorithm has high communication cost and requires the server to facilitate interaction between the users. Finally, we describe an algorithm for estimating collision entropy that generalizes the best known algorithm to the private and communication-efficient setting.
Label differential privacy via clustering
Oct 05, 2021
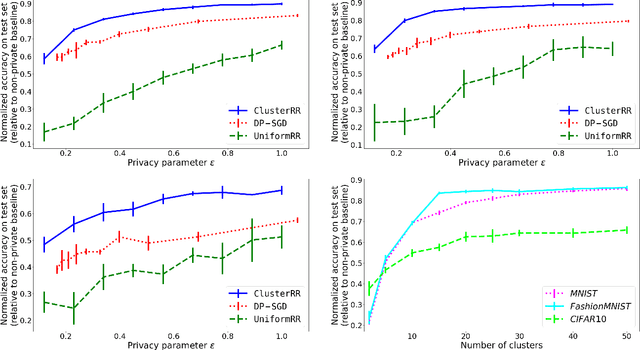
Abstract:We present new mechanisms for \emph{label differential privacy}, a relaxation of differentially private machine learning that only protects the privacy of the labels in the training set. Our mechanisms cluster the examples in the training set using their (non-private) feature vectors, randomly re-sample each label from examples in the same cluster, and output a training set with noisy labels as well as a modified version of the true loss function. We prove that when the clusters are both large and high-quality, the model that minimizes the modified loss on the noisy training set converges to small excess risk at a rate that is comparable to the rate for non-private learning. We describe both a centralized mechanism in which the entire training set is stored by a trusted curator, and a distributed mechanism where each user stores a single labeled example and replaces her label with the label of a randomly selected user from the same cluster. We also describe a learning problem in which large clusters are necessary to achieve both strong privacy and either good precision or good recall. Our experiments show that randomizing the labels within each cluster significantly improves the privacy vs. accuracy trade-off compared to applying uniform randomized response to the labels, and also compared to learning a model via DP-SGD.
Private Optimization Without Constraint Violations
Jul 02, 2020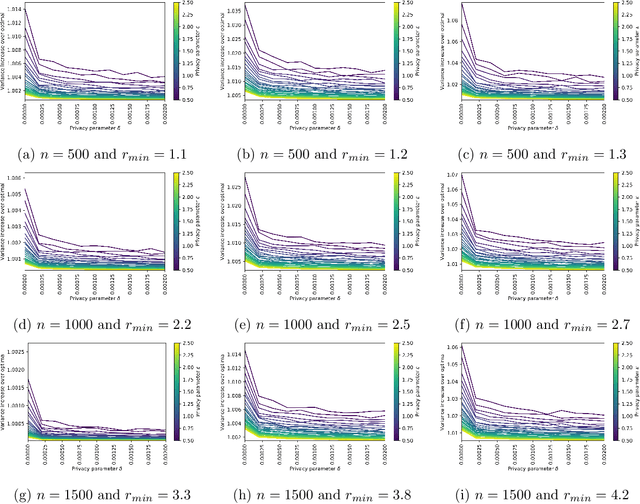
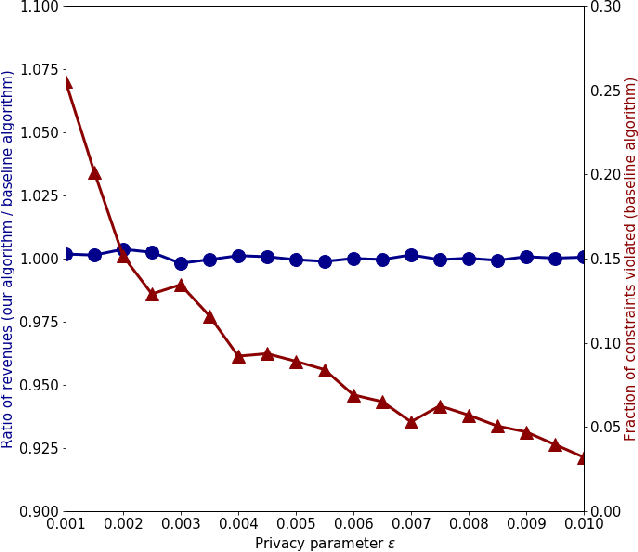
Abstract:We study the problem of differentially private optimization with linear constraints when the right-hand-side of the constraints depends on private data. This type of problem appears in many applications, especially resource allocation. Previous research provided solutions that retained privacy, but sometimes violated the constraints. In many settings, however, the constraints cannot be violated under any circumstances. To address this hard requirement, we present an algorithm that releases a nearly-optimal solution satisfying the problem's constraints with probability 1. We also prove a lower bound demonstrating that the difference between the objective value of our algorithm's solution and the optimal solution is tight up to logarithmic factors among all differentially private algorithms. We conclude with experiments on real and synthetic datasets demonstrating that our algorithm can achieve nearly optimal performance while preserving privacy.
Statistical Cost Sharing
Mar 09, 2017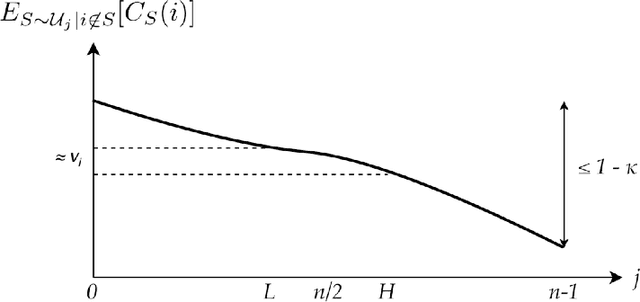
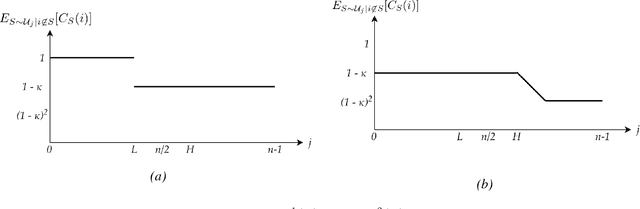
Abstract:We study the cost sharing problem for cooperative games in situations where the cost function $C$ is not available via oracle queries, but must instead be derived from data, represented as tuples $(S, C(S))$, for different subsets $S$ of players. We formalize this approach, which we call statistical cost sharing, and consider the computation of the core and the Shapley value, when the tuples are drawn from some distribution $\mathcal{D}$. Previous work by Balcan et al. in this setting showed how to compute cost shares that satisfy the core property with high probability for limited classes of functions. We expand on their work and give an algorithm that computes such cost shares for any function with a non-empty core. We complement these results by proving an inapproximability lower bound for a weaker relaxation. We then turn our attention to the Shapley value. We first show that when cost functions come from the family of submodular functions with bounded curvature, $\kappa$, the Shapley value can be approximated from samples up to a $\sqrt{1 - \kappa}$ factor, and that the bound is tight. We then define statistical analogues of the Shapley axioms, and derive a notion of statistical Shapley value. We show that these can always be approximated arbitrarily well for general functions over any distribution $\mathcal{D}$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge