Private Optimization Without Constraint Violations

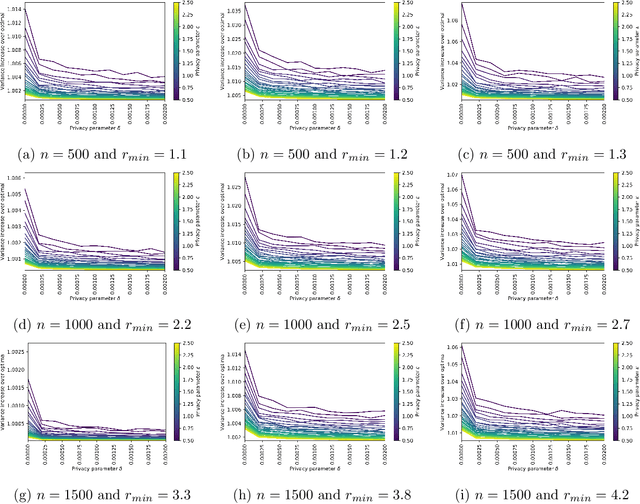
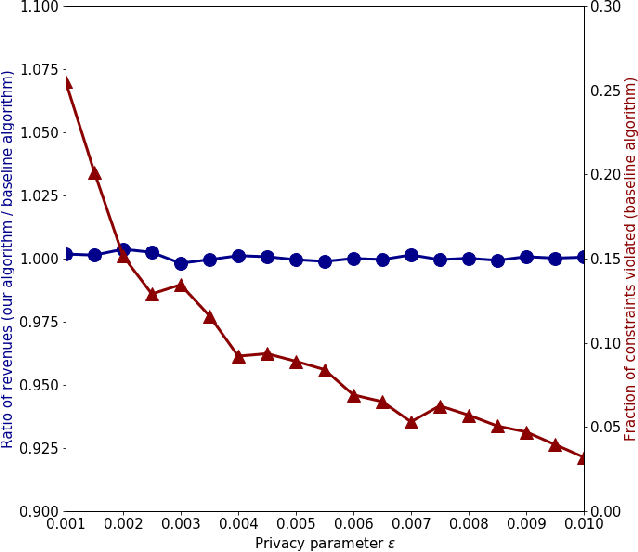
We study the problem of differentially private optimization with linear constraints when the right-hand-side of the constraints depends on private data. This type of problem appears in many applications, especially resource allocation. Previous research provided solutions that retained privacy, but sometimes violated the constraints. In many settings, however, the constraints cannot be violated under any circumstances. To address this hard requirement, we present an algorithm that releases a nearly-optimal solution satisfying the problem's constraints with probability 1. We also prove a lower bound demonstrating that the difference between the objective value of our algorithm's solution and the optimal solution is tight up to logarithmic factors among all differentially private algorithms. We conclude with experiments on real and synthetic datasets demonstrating that our algorithm can achieve nearly optimal performance while preserving privacy.