Private and Communication-Efficient Algorithms for Entropy Estimation

Modern statistical estimation is often performed in a distributed setting where each sample belongs to a single user who shares their data with a central server. Users are typically concerned with preserving the privacy of their samples, and also with minimizing the amount of data they must transmit to the server. We give improved private and communication-efficient algorithms for estimating several popular measures of the entropy of a distribution. All of our algorithms have constant communication cost and satisfy local differential privacy. For a joint distribution over many variables whose conditional independence is given by a tree, we describe algorithms for estimating Shannon entropy that require a number of samples that is linear in the number of variables, compared to the quadratic sample complexity of prior work. We also describe an algorithm for estimating Gini entropy whose sample complexity has no dependence on the support size of the distribution and can be implemented using a single round of concurrent communication between the users and the server. In contrast, the previously best-known algorithm has high communication cost and requires the server to facilitate interaction between the users. Finally, we describe an algorithm for estimating collision entropy that generalizes the best known algorithm to the private and communication-efficient setting.

Adaptation Algorithm and Theory Based on Generalized Discrepancy

We present a new algorithm for domain adaptation improving upon a discrepancy minimization algorithm previously shown to outperform a number of algorithms for this task. Unlike many previous algorithms for domain adaptation, our algorithm does not consist of a fixed reweighting of the losses over the training sample. We show that our algorithm benefits from a solid theoretical foundation and more favorable learning bounds than discrepancy minimization. We present a detailed description of our algorithm and give several efficient solutions for solving its optimization problem. We also report the results of several experiments showing that it outperforms discrepancy minimization.

Learning Theory and Algorithms for Revenue Optimization in Second-Price Auctions with Reserve

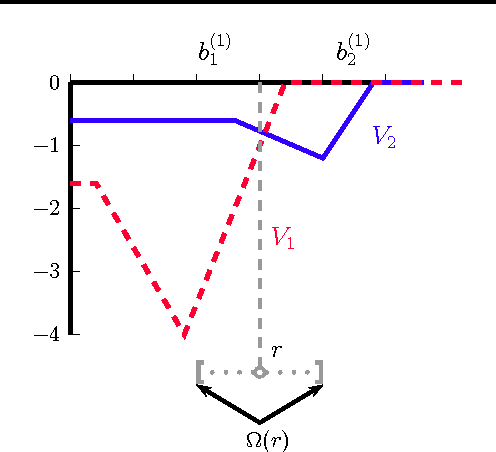
Second-price auctions with reserve play a critical role for modern search engine and popular online sites since the revenue of these companies often directly de- pends on the outcome of such auctions. The choice of the reserve price is the main mechanism through which the auction revenue can be influenced in these electronic markets. We cast the problem of selecting the reserve price to optimize revenue as a learning problem and present a full theoretical analysis dealing with the complex properties of the corresponding loss function. We further give novel algorithms for solving this problem and report the results of several experiments in both synthetic and real data demonstrating their effectiveness.

Revenue Optimization in Posted-Price Auctions with Strategic Buyers

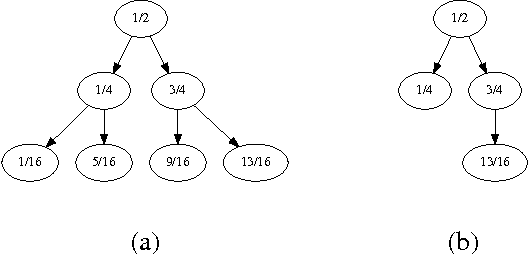
We study revenue optimization learning algorithms for posted-price auctions with strategic buyers. We analyze a very broad family of monotone regret minimization algorithms for this problem, which includes the previously best known algorithm, and show that no algorithm in that family admits a strategic regret more favorable than $\Omega(\sqrt{T})$. We then introduce a new algorithm that achieves a strategic regret differing from the lower bound only by a factor in $O(\log T)$, an exponential improvement upon the previous best algorithm. Our new algorithm admits a natural analysis and simpler proofs, and the ideas behind its design are general. We also report the results of empirical evaluations comparing our algorithm with the previous state of the art and show a consistent exponential improvement in several different scenarios.