A Scalable Crawling Algorithm Utilizing Noisy Change-Indicating Signals

Web refresh crawling is the problem of keeping a cache of web pages fresh, that is, having the most recent copy available when a page is requested, given a limited bandwidth available to the crawler. Under the assumption that the change and request events, resp., to each web page follow independent Poisson processes, the optimal scheduling policy was derived by Azar et al. 2018. In this paper, we study an extension of this problem where side information indicating content changes, such as various types of web pings, for example, signals from sitemaps, content delivery networks, etc., is available. Incorporating such side information into the crawling policy is challenging, because (i) the signals can be noisy with false positive events and with missing change events; and (ii) the crawler should achieve a fair performance over web pages regardless of the quality of the side information, which might differ from web page to web page. We propose a scalable crawling algorithm which (i) uses the noisy side information in an optimal way under mild assumptions; (ii) can be deployed without heavy centralized computation; (iii) is able to crawl web pages at a constant total rate without spikes in the total bandwidth usage over any time interval, and automatically adapt to the new optimal solution when the total bandwidth changes without centralized computation. Experiments clearly demonstrate the versatility of our approach.

Private and Communication-Efficient Algorithms for Entropy Estimation

Modern statistical estimation is often performed in a distributed setting where each sample belongs to a single user who shares their data with a central server. Users are typically concerned with preserving the privacy of their samples, and also with minimizing the amount of data they must transmit to the server. We give improved private and communication-efficient algorithms for estimating several popular measures of the entropy of a distribution. All of our algorithms have constant communication cost and satisfy local differential privacy. For a joint distribution over many variables whose conditional independence is given by a tree, we describe algorithms for estimating Shannon entropy that require a number of samples that is linear in the number of variables, compared to the quadratic sample complexity of prior work. We also describe an algorithm for estimating Gini entropy whose sample complexity has no dependence on the support size of the distribution and can be implemented using a single round of concurrent communication between the users and the server. In contrast, the previously best-known algorithm has high communication cost and requires the server to facilitate interaction between the users. Finally, we describe an algorithm for estimating collision entropy that generalizes the best known algorithm to the private and communication-efficient setting.

Optimal Learning of Mallows Block Model

The Mallows model, introduced in the seminal paper of Mallows 1957, is one of the most fundamental ranking distribution over the symmetric group $S_m$. To analyze more complex ranking data, several studies considered the Generalized Mallows model defined by Fligner and Verducci 1986. Despite the significant research interest of ranking distributions, the exact sample complexity of estimating the parameters of a Mallows and a Generalized Mallows Model is not well-understood. The main result of the paper is a tight sample complexity bound for learning Mallows and Generalized Mallows Model. We approach the learning problem by analyzing a more general model which interpolates between the single parameter Mallows Model and the $m$ parameter Mallows model. We call our model Mallows Block Model -- referring to the Block Models that are a popular model in theoretical statistics. Our sample complexity analysis gives tight bound for learning the Mallows Block Model for any number of blocks. We provide essentially matching lower bounds for our sample complexity results. As a corollary of our analysis, it turns out that, if the central ranking is known, one single sample from the Mallows Block Model is sufficient to estimate the spread parameters with error that goes to zero as the size of the permutations goes to infinity. In addition, we calculate the exact rate of the parameter estimation error.

A no-regret generalization of hierarchical softmax to extreme multi-label classification

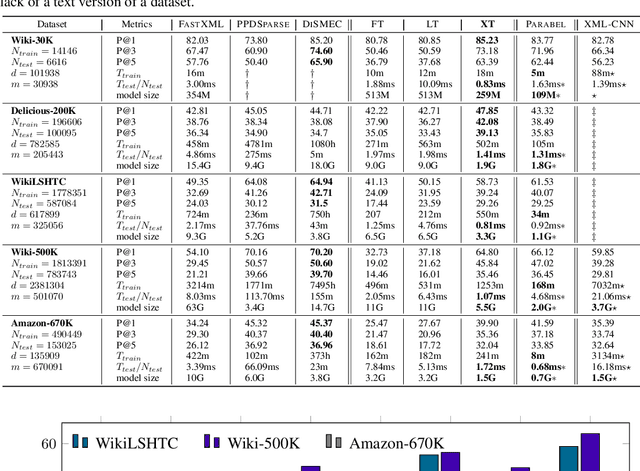
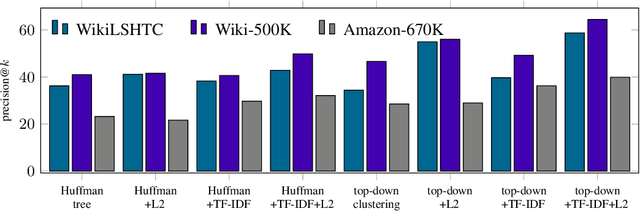
Extreme multi-label classification (XMLC) is a problem of tagging an instance with a small subset of relevant labels chosen from an extremely large pool of possible labels. Large label spaces can be efficiently handled by organizing labels as a tree, like in the hierarchical softmax (HSM) approach commonly used for multi-class problems. In this paper, we investigate probabilistic label trees (PLTs) that have been recently devised for tackling XMLC problems. We show that PLTs are a no-regret multi-label generalization of HSM when precision@k is used as a model evaluation metric. Critically, we prove that pick-one-label heuristic - a reduction technique from multi-label to multi-class that is routinely used along with HSM - is not consistent in general. We also show that our implementation of PLTs, referred to as extremeText (XT), obtains significantly better results than HSM with the pick-one-label heuristic and XML-CNN, a deep network specifically designed for XMLC problems. Moreover, XT is competitive to many state-of-the-art approaches in terms of statistical performance, model size and prediction time which makes it amenable to deploy in an online system.