Query and Conquer: Execution-Guided SQL Generation

We propose a novel approach for generating complex outputs that significantly improves accuracy in text-to-SQL tasks. Our method leverages execution results to select the most semantically consistent query from multiple candidates, enabling smaller, cost-effective models to surpass computationally intensive reasoning methods such as o1, o3-mini, and DeepSeek R1 while reducing inference cost by as much as 30 times. It integrates effortlessly with existing models, offering a practical and scalable pathway to state-of-the-art SQL generation.

Tackling prediction tasks in relational databases with LLMs

Though large language models (LLMs) have demonstrated exceptional performance across numerous problems, their application to predictive tasks in relational databases remains largely unexplored. In this work, we address the notion that LLMs cannot yield satisfactory results on relational databases due to their interconnected tables, complex relationships, and heterogeneous data types. Using the recently introduced RelBench benchmark, we demonstrate that even a straightforward application of LLMs achieves competitive performance on these tasks. These findings establish LLMs as a promising new baseline for ML on relational databases and encourage further research in this direction.

Multilingual hierarchical classification of job advertisements for job vacancy statistics

The goal of this paper is to develop a multilingual classifier and conditional probability estimator of occupation codes for online job advertisements according in accordance with the International Standard Classification of Occupations (ISCO) extended with the Polish Classification of Occupations and Specializations (KZiS), which is analogous to the European Classification of Occupations. In this paper, we utilise a range of data sources, including a novel one, namely the Central Job Offers Database, which is a register of all vacancies submitted to Public Employment Offices. Their staff members code the vacancies according to the ISCO and KZiS. A hierarchical multi-class classifier has been developed based on the transformer architecture. The classifier begins by encoding the jobs found in advertisements to the widest 1-digit occupational group, and then narrows the assignment to a 6-digit occupation code. We show that incorporation of the hierarchical structure of occupations improves prediction accuracy by 1-2 percentage points, particularly for the hand-coded online job advertisements. Finally, a bilingual (Polish and English) and multilingual (24 languages) model is developed based on data translated using closed and open-source software. The open-source software is provided for the benefit of the official statistics community, with a particular focus on international comparability.

A General Online Algorithm for Optimizing Complex Performance Metrics

We consider sequential maximization of performance metrics that are general functions of a confusion matrix of a classifier (such as precision, F-measure, or G-mean). Such metrics are, in general, non-decomposable over individual instances, making their optimization very challenging. While they have been extensively studied under different frameworks in the batch setting, their analysis in the online learning regime is very limited, with only a few distinguished exceptions. In this paper, we introduce and analyze a general online algorithm that can be used in a straightforward way with a variety of complex performance metrics in binary, multi-class, and multi-label classification problems. The algorithm's update and prediction rules are appealingly simple and computationally efficient without the need to store any past data. We show the algorithm attains $\mathcal{O}(\frac{\ln n}{n})$ regret for concave and smooth metrics and verify the efficiency of the proposed algorithm in empirical studies.

Consistent algorithms for multi-label classification with macro-at-$k$ metrics

We consider the optimization of complex performance metrics in multi-label classification under the population utility framework. We mainly focus on metrics linearly decomposable into a sum of binary classification utilities applied separately to each label with an additional requirement of exactly $k$ labels predicted for each instance. These "macro-at-$k$" metrics possess desired properties for extreme classification problems with long tail labels. Unfortunately, the at-$k$ constraint couples the otherwise independent binary classification tasks, leading to a much more challenging optimization problem than standard macro-averages. We provide a statistical framework to study this problem, prove the existence and the form of the optimal classifier, and propose a statistically consistent and practical learning algorithm based on the Frank-Wolfe method. Interestingly, our main results concern even more general metrics being non-linear functions of label-wise confusion matrices. Empirical results provide evidence for the competitive performance of the proposed approach.

Generalized test utilities for long-tail performance in extreme multi-label classification

Extreme multi-label classification (XMLC) is the task of selecting a small subset of relevant labels from a very large set of possible labels. As such, it is characterized by long-tail labels, i.e., most labels have very few positive instances. With standard performance measures such as precision@k, a classifier can ignore tail labels and still report good performance. However, it is often argued that correct predictions in the tail are more interesting or rewarding, but the community has not yet settled on a metric capturing this intuitive concept. The existing propensity-scored metrics fall short on this goal by confounding the problems of long-tail and missing labels. In this paper, we analyze generalized metrics budgeted "at k" as an alternative solution. To tackle the challenging problem of optimizing these metrics, we formulate it in the expected test utility (ETU) framework, which aims at optimizing the expected performance on a fixed test set. We derive optimal prediction rules and construct computationally efficient approximations with provable regret guarantees and robustness against model misspecification. Our algorithm, based on block coordinate ascent, scales effortlessly to XMLC problems and obtains promising results in terms of long-tail performance.

On Missing Labels, Long-tails and Propensities in Extreme Multi-label Classification

The propensity model introduced by Jain et al. 2016 has become a standard approach for dealing with missing and long-tail labels in extreme multi-label classification (XMLC). In this paper, we critically revise this approach showing that despite its theoretical soundness, its application in contemporary XMLC works is debatable. We exhaustively discuss the flaws of the propensity-based approach, and present several recipes, some of them related to solutions used in search engines and recommender systems, that we believe constitute promising alternatives to be followed in XMLC.

Propensity-scored Probabilistic Label Trees

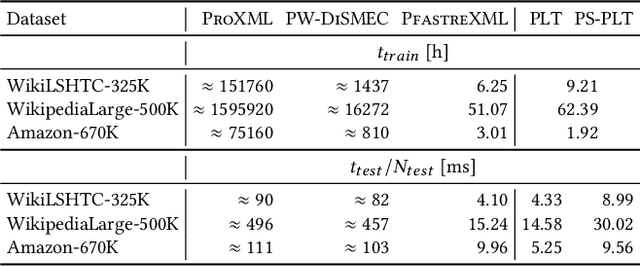
Extreme multi-label classification (XMLC) refers to the task of tagging instances with small subsets of relevant labels coming from an extremely large set of all possible labels. Recently, XMLC has been widely applied to diverse web applications such as automatic content labeling, online advertising, or recommendation systems. In such environments, label distribution is often highly imbalanced, consisting mostly of very rare tail labels, and relevant labels can be missing. As a remedy to these problems, the propensity model has been introduced and applied within several XMLC algorithms. In this work, we focus on the problem of optimal predictions under this model for probabilistic label trees, a popular approach for XMLC problems. We introduce an inference procedure, based on the $A^*$-search algorithm, that efficiently finds the optimal solution, assuming that all probabilities and propensities are known. We demonstrate the attractiveness of this approach in a wide empirical study on popular XMLC benchmark datasets.

Probabilistic Label Trees for Extreme Multi-label Classification

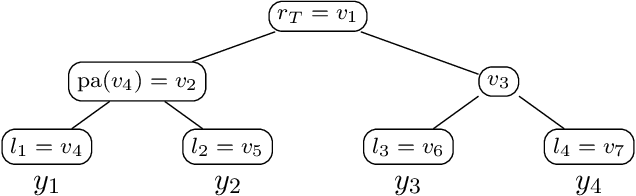
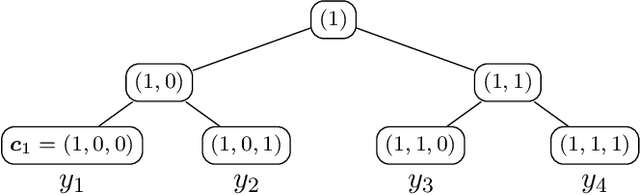
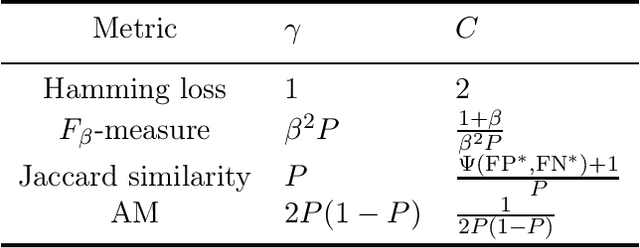
Extreme multi-label classification (XMLC) is a learning task of tagging instances with a small subset of relevant labels chosen from an extremely large pool of possible labels. Problems of this scale can be efficiently handled by organizing labels as a tree, like in hierarchical softmax used for multi-class problems. In this paper, we thoroughly investigate probabilistic label trees (PLTs) which can be treated as a generalization of hierarchical softmax for multi-label problems. We first introduce the PLT model and discuss training and inference procedures and their computational costs. Next, we prove the consistency of PLTs for a wide spectrum of performance metrics. To this end, we upperbound their regret by a function of surrogate-loss regrets of node classifiers. Furthermore, we consider a problem of training PLTs in a fully online setting, without any prior knowledge of training instances, their features, or labels. In this case, both node classifiers and the tree structure are trained online. We prove a specific equivalence between the fully online algorithm and an algorithm with a tree structure given in advance. Finally, we discuss several implementations of PLTs and introduce a new one, napkinXC, which we empirically evaluate and compare with state-of-the-art algorithms.

Online probabilistic label trees

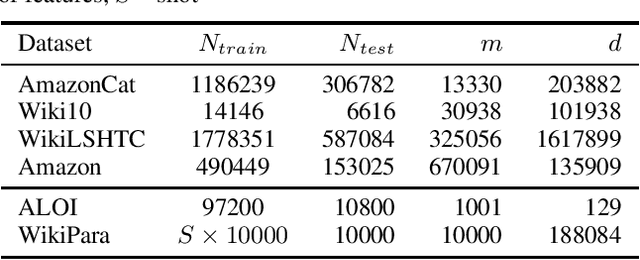
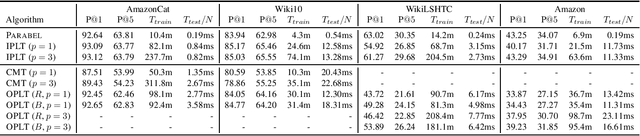
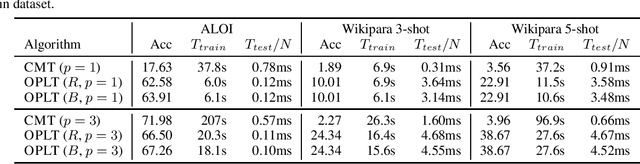
We introduce online probabilistic label trees (OPLTs), an algorithm that trains a label tree classifier in a fully online manner, without any prior knowledge about the number of training instances, their features and labels. OPLTs are characterized by low time and space complexity as well as strong theoretical guarantees. They can be used for online multi-label and multi-class classification, including the very challenging scenarios of one- or few-shot learning. We demonstrate the attractiveness of OPLTs in a wide empirical study on several instances of the tasks mentioned above.