Kalina Jasinska-Kobus
Propensity-scored Probabilistic Label Trees
Oct 20, 2021
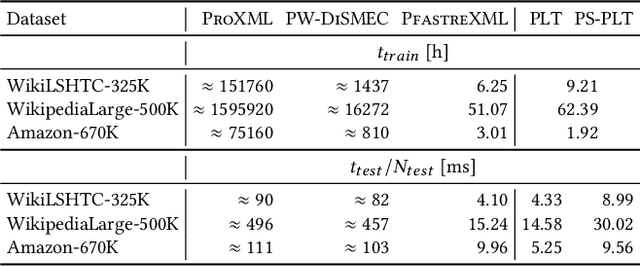
Abstract:Extreme multi-label classification (XMLC) refers to the task of tagging instances with small subsets of relevant labels coming from an extremely large set of all possible labels. Recently, XMLC has been widely applied to diverse web applications such as automatic content labeling, online advertising, or recommendation systems. In such environments, label distribution is often highly imbalanced, consisting mostly of very rare tail labels, and relevant labels can be missing. As a remedy to these problems, the propensity model has been introduced and applied within several XMLC algorithms. In this work, we focus on the problem of optimal predictions under this model for probabilistic label trees, a popular approach for XMLC problems. We introduce an inference procedure, based on the $A^*$-search algorithm, that efficiently finds the optimal solution, assuming that all probabilities and propensities are known. We demonstrate the attractiveness of this approach in a wide empirical study on popular XMLC benchmark datasets.
Probabilistic Label Trees for Extreme Multi-label Classification
Sep 23, 2020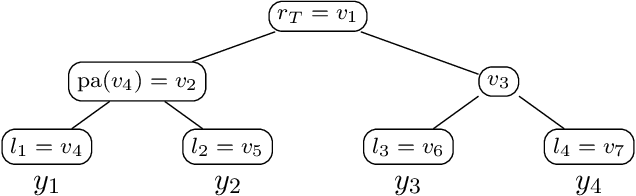

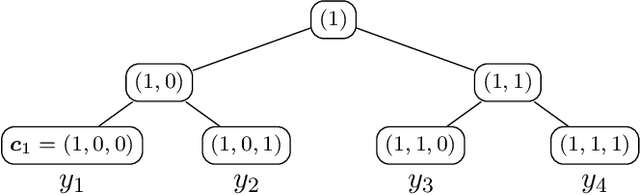
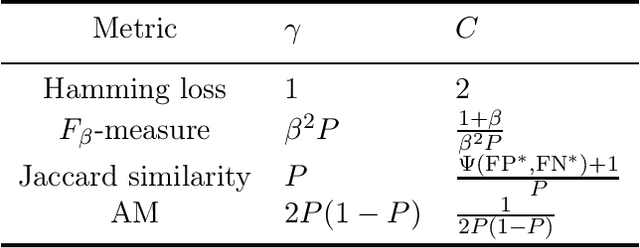
Abstract:Extreme multi-label classification (XMLC) is a learning task of tagging instances with a small subset of relevant labels chosen from an extremely large pool of possible labels. Problems of this scale can be efficiently handled by organizing labels as a tree, like in hierarchical softmax used for multi-class problems. In this paper, we thoroughly investigate probabilistic label trees (PLTs) which can be treated as a generalization of hierarchical softmax for multi-label problems. We first introduce the PLT model and discuss training and inference procedures and their computational costs. Next, we prove the consistency of PLTs for a wide spectrum of performance metrics. To this end, we upperbound their regret by a function of surrogate-loss regrets of node classifiers. Furthermore, we consider a problem of training PLTs in a fully online setting, without any prior knowledge of training instances, their features, or labels. In this case, both node classifiers and the tree structure are trained online. We prove a specific equivalence between the fully online algorithm and an algorithm with a tree structure given in advance. Finally, we discuss several implementations of PLTs and introduce a new one, napkinXC, which we empirically evaluate and compare with state-of-the-art algorithms.
Online probabilistic label trees
Jul 08, 2020
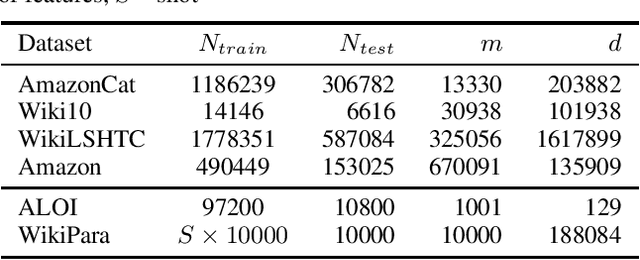
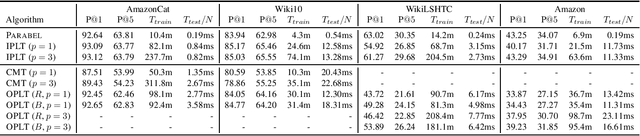
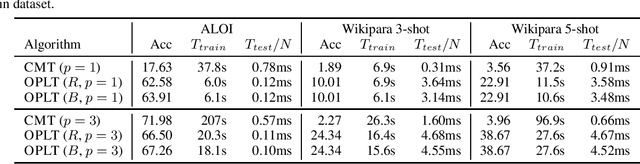
Abstract:We introduce online probabilistic label trees (OPLTs), an algorithm that trains a label tree classifier in a fully online manner, without any prior knowledge about the number of training instances, their features and labels. OPLTs are characterized by low time and space complexity as well as strong theoretical guarantees. They can be used for online multi-label and multi-class classification, including the very challenging scenarios of one- or few-shot learning. We demonstrate the attractiveness of OPLTs in a wide empirical study on several instances of the tasks mentioned above.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge