Optimal Downsampling for Imbalanced Classification with Generalized Linear Models

Downsampling or under-sampling is a technique that is utilized in the context of large and highly imbalanced classification models. We study optimal downsampling for imbalanced classification using generalized linear models (GLMs). We propose a pseudo maximum likelihood estimator and study its asymptotic normality in the context of increasingly imbalanced populations relative to an increasingly large sample size. We provide theoretical guarantees for the introduced estimator. Additionally, we compute the optimal downsampling rate using a criterion that balances statistical accuracy and computational efficiency. Our numerical experiments, conducted on both synthetic and empirical data, further validate our theoretical results, and demonstrate that the introduced estimator outperforms commonly available alternatives.

Probabilistic Label Trees for Extreme Multi-label Classification

Extreme multi-label classification (XMLC) is a learning task of tagging instances with a small subset of relevant labels chosen from an extremely large pool of possible labels. Problems of this scale can be efficiently handled by organizing labels as a tree, like in hierarchical softmax used for multi-class problems. In this paper, we thoroughly investigate probabilistic label trees (PLTs) which can be treated as a generalization of hierarchical softmax for multi-label problems. We first introduce the PLT model and discuss training and inference procedures and their computational costs. Next, we prove the consistency of PLTs for a wide spectrum of performance metrics. To this end, we upperbound their regret by a function of surrogate-loss regrets of node classifiers. Furthermore, we consider a problem of training PLTs in a fully online setting, without any prior knowledge of training instances, their features, or labels. In this case, both node classifiers and the tree structure are trained online. We prove a specific equivalence between the fully online algorithm and an algorithm with a tree structure given in advance. Finally, we discuss several implementations of PLTs and introduce a new one, napkinXC, which we empirically evaluate and compare with state-of-the-art algorithms.

On the computational complexity of the probabilistic label tree algorithms

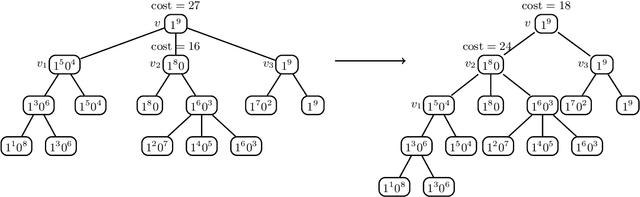
Label tree-based algorithms are widely used to tackle multi-class and multi-label problems with a large number of labels. We focus on a particular subclass of these algorithms that use probabilistic classifiers in the tree nodes. Examples of such algorithms are hierarchical softmax (HSM), designed for multi-class classification, and probabilistic label trees (PLTs) that generalize HSM to multi-label problems. If the tree structure is given, learning of PLT can be solved with provable regret guaranties [Wydmuch et.al. 2018]. However, to find a tree structure that results in a PLT with a low training and prediction computational costs as well as low statistical error seems to be a very challenging problem, not well-understood yet. In this paper, we address the problem of finding a tree structure that has low computational cost. First, we show that finding a tree with optimal training cost is NP-complete, nevertheless there are some tractable special cases with either perfect approximation or exact solution that can be obtained in linear time in terms of the number of labels $m$. For the general case, we obtain $O(\log m)$ approximation in linear time too. Moreover, we prove an upper bound on the expected prediction cost expressed in terms of the expected training cost. We also show that under additional assumptions the prediction cost of a PLT is $O(\log m)$.

Multi-Target Prediction: A Unifying View on Problems and Methods

Multi-target prediction (MTP) is concerned with the simultaneous prediction of multiple target variables of diverse type. Due to its enormous application potential, it has developed into an active and rapidly expanding research field that combines several subfields of machine learning, including multivariate regression, multi-label classification, multi-task learning, dyadic prediction, zero-shot learning, network inference, and matrix completion. In this paper, we present a unifying view on MTP problems and methods. First, we formally discuss commonalities and differences between existing MTP problems. To this end, we introduce a general framework that covers the above subfields as special cases. As a second contribution, we provide a structured overview of MTP methods. This is accomplished by identifying a number of key properties, which distinguish such methods and determine their suitability for different types of problems. Finally, we also discuss a few challenges for future research.

Exact and efficient top-K inference for multi-target prediction by querying separable linear relational models

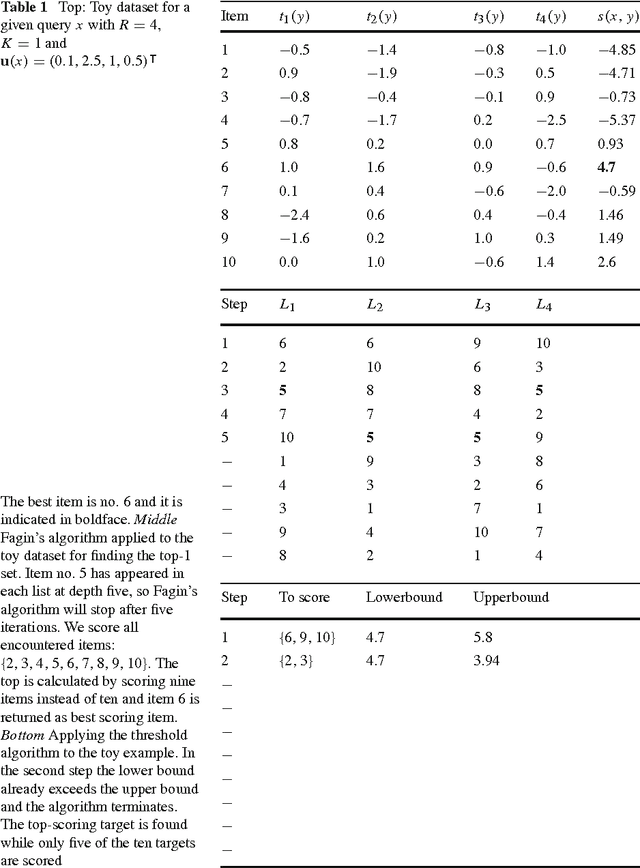
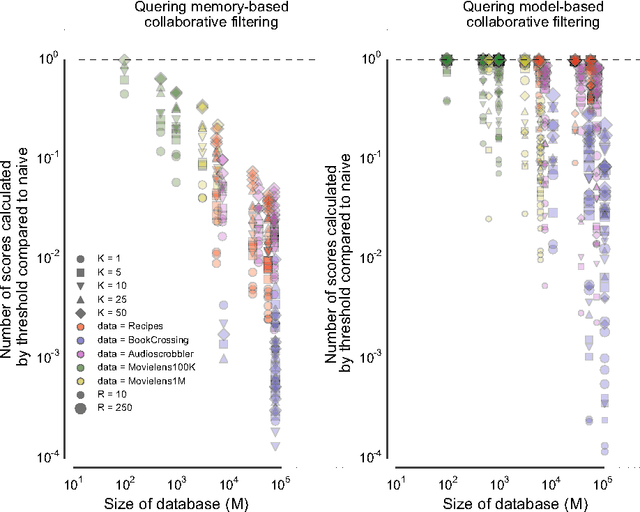
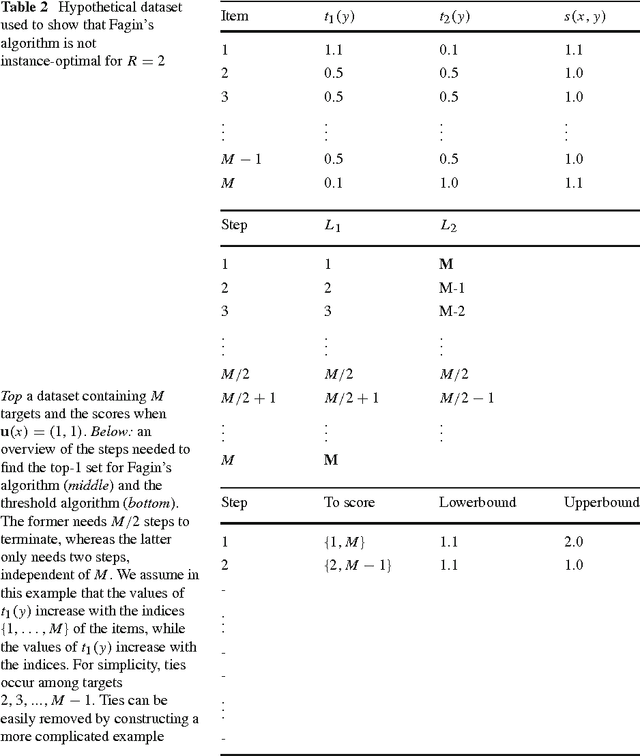
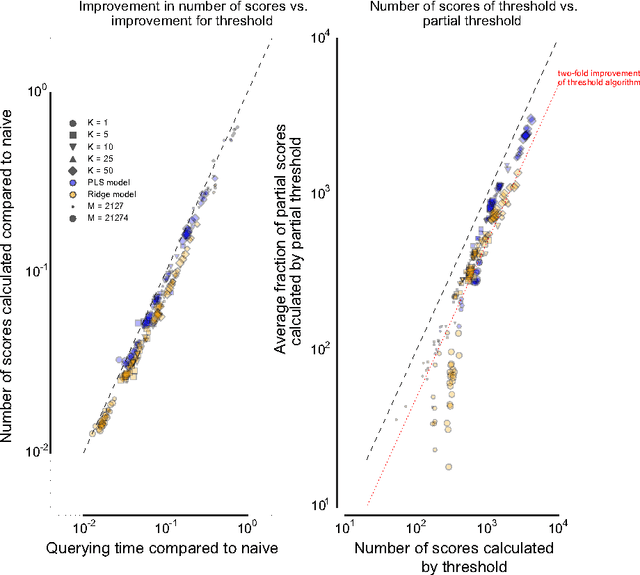
Many complex multi-target prediction problems that concern large target spaces are characterised by a need for efficient prediction strategies that avoid the computation of predictions for all targets explicitly. Examples of such problems emerge in several subfields of machine learning, such as collaborative filtering, multi-label classification, dyadic prediction and biological network inference. In this article we analyse efficient and exact algorithms for computing the top-$K$ predictions in the above problem settings, using a general class of models that we refer to as separable linear relational models. We show how to use those inference algorithms, which are modifications of well-known information retrieval methods, in a variety of machine learning settings. Furthermore, we study the possibility of scoring items incompletely, while still retaining an exact top-K retrieval. Experimental results in several application domains reveal that the so-called threshold algorithm is very scalable, performing often many orders of magnitude more efficiently than the naive approach.

On the Bayes-optimality of F-measure maximizers

The F-measure, which has originally been introduced in information retrieval, is nowadays routinely used as a performance metric for problems such as binary classification, multi-label classification, and structured output prediction. Optimizing this measure is a statistically and computationally challenging problem, since no closed-form solution exists. Adopting a decision-theoretic perspective, this article provides a formal and experimental analysis of different approaches for maximizing the F-measure. We start with a Bayes-risk analysis of related loss functions, such as Hamming loss and subset zero-one loss, showing that optimizing such losses as a surrogate of the F-measure leads to a high worst-case regret. Subsequently, we perform a similar type of analysis for F-measure maximizing algorithms, showing that such algorithms are approximate, while relying on additional assumptions regarding the statistical distribution of the binary response variables. Furthermore, we present a new algorithm which is not only computationally efficient but also Bayes-optimal, regardless of the underlying distribution. To this end, the algorithm requires only a quadratic (with respect to the number of binary responses) number of parameters of the joint distribution. We illustrate the practical performance of all analyzed methods by means of experiments with multi-label classification problems.

Consistent Multilabel Ranking through Univariate Losses

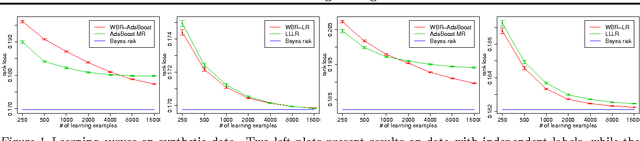
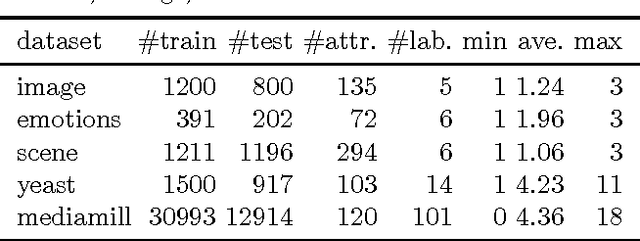
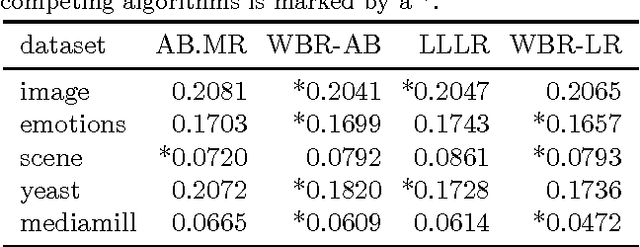
We consider the problem of rank loss minimization in the setting of multilabel classification, which is usually tackled by means of convex surrogate losses defined on pairs of labels. Very recently, this approach was put into question by a negative result showing that commonly used pairwise surrogate losses, such as exponential and logistic losses, are inconsistent. In this paper, we show a positive result which is arguably surprising in light of the previous one: the simpler univariate variants of exponential and logistic surrogates (i.e., defined on single labels) are consistent for rank loss minimization. Instead of directly proving convergence, we give a much stronger result by deriving regret bounds and convergence rates. The proposed losses suggest efficient and scalable algorithms, which are tested experimentally.