Data-Driven Probabilistic Evaluation of Logic Properties with PAC-Confidence on Mealy Machines

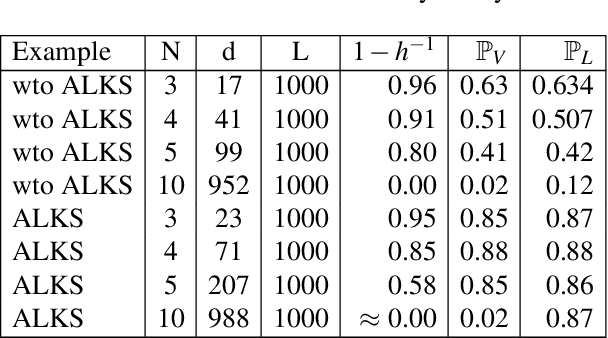
Cyber-Physical Systems (CPS) are complex systems that require powerful models for tasks like verification, diagnosis, or debugging. Often, suitable models are not available and manual extraction is difficult. Data-driven approaches then provide a solution to, e.g., diagnosis tasks and verification problems based on data collected from the system. In this paper, we consider CPS with a discrete abstraction in the form of a Mealy machine. We propose a data-driven approach to determine the safety probability of the system on a finite horizon of n time steps. The approach is based on the Probably Approximately Correct (PAC) learning paradigm. Thus, we elaborate a connection between discrete logic and probabilistic reachability analysis of systems, especially providing an additional confidence on the determined probability. The learning process follows an active learning paradigm, where new learning data is sampled in a guided way after an initial learning set is collected. We validate the approach with a case study on an automated lane-keeping system.

Multi-Target Prediction: A Unifying View on Problems and Methods

Multi-target prediction (MTP) is concerned with the simultaneous prediction of multiple target variables of diverse type. Due to its enormous application potential, it has developed into an active and rapidly expanding research field that combines several subfields of machine learning, including multivariate regression, multi-label classification, multi-task learning, dyadic prediction, zero-shot learning, network inference, and matrix completion. In this paper, we present a unifying view on MTP problems and methods. First, we formally discuss commonalities and differences between existing MTP problems. To this end, we introduce a general framework that covers the above subfields as special cases. As a second contribution, we provide a structured overview of MTP methods. This is accomplished by identifying a number of key properties, which distinguish such methods and determine their suitability for different types of problems. Finally, we also discuss a few challenges for future research.

Consistent Multilabel Ranking through Univariate Losses

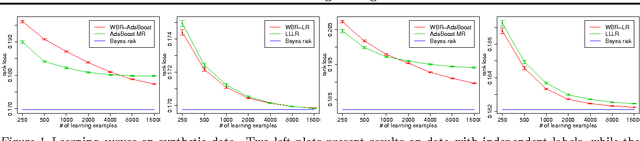
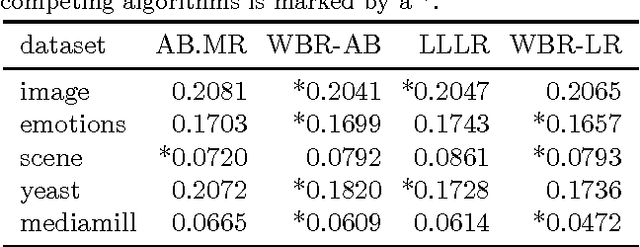
We consider the problem of rank loss minimization in the setting of multilabel classification, which is usually tackled by means of convex surrogate losses defined on pairs of labels. Very recently, this approach was put into question by a negative result showing that commonly used pairwise surrogate losses, such as exponential and logistic losses, are inconsistent. In this paper, we show a positive result which is arguably surprising in light of the previous one: the simpler univariate variants of exponential and logistic surrogates (i.e., defined on single labels) are consistent for rank loss minimization. Instead of directly proving convergence, we give a much stronger result by deriving regret bounds and convergence rates. The proposed losses suggest efficient and scalable algorithms, which are tested experimentally.