The CausalBench challenge: A machine learning contest for gene network inference from single-cell perturbation data

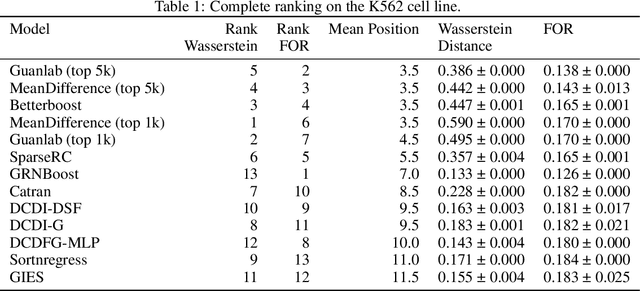
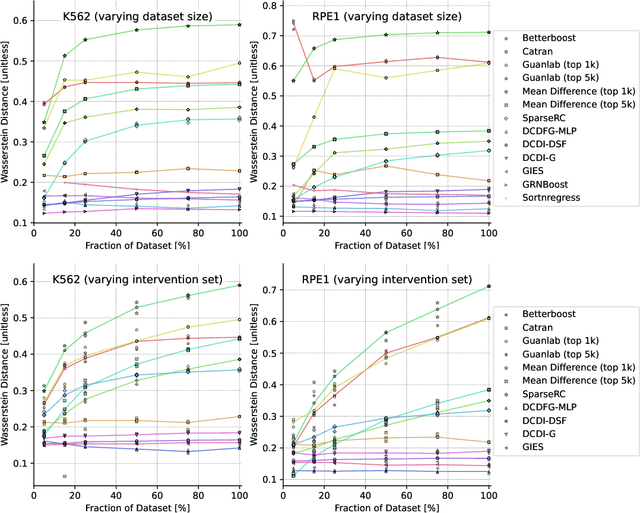
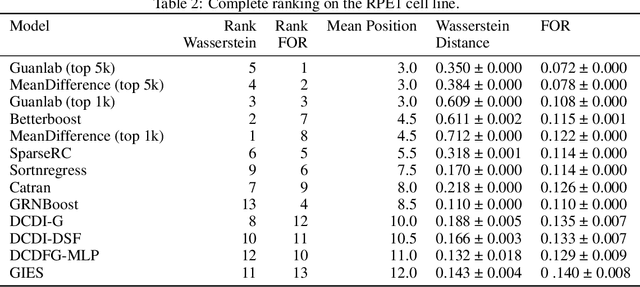
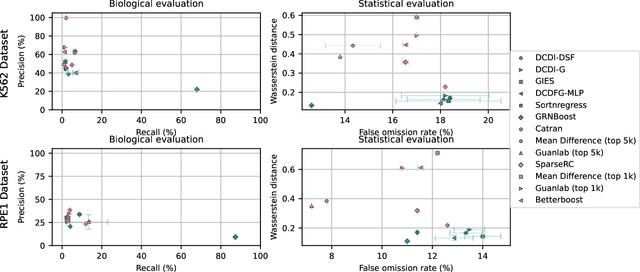
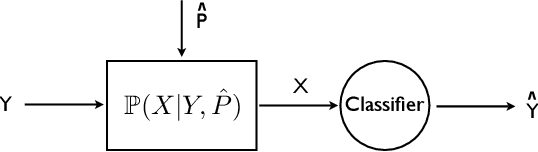
In drug discovery, mapping interactions between genes within cellular systems is a crucial early step. This helps formulate hypotheses regarding molecular mechanisms that could potentially be targeted by future medicines. The CausalBench Challenge was an initiative to invite the machine learning community to advance the state of the art in constructing gene-gene interaction networks. These networks, derived from large-scale, real-world datasets of single cells under various perturbations, are crucial for understanding the causal mechanisms underlying disease biology. Using the framework provided by the CausalBench benchmark, participants were tasked with enhancing the capacity of the state of the art methods to leverage large-scale genetic perturbation data. This report provides an analysis and summary of the methods submitted during the challenge to give a partial image of the state of the art at the time of the challenge. The winning solutions significantly improved performance compared to previous baselines, establishing a new state of the art for this critical task in biology and medicine.

Learning to Crawl

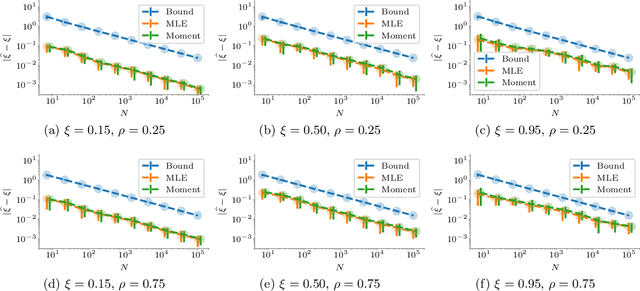
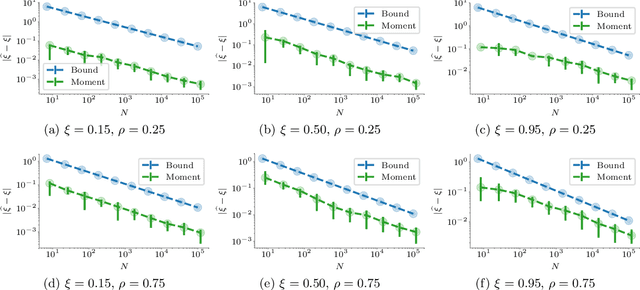
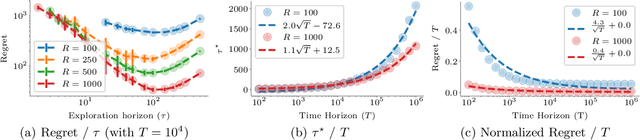
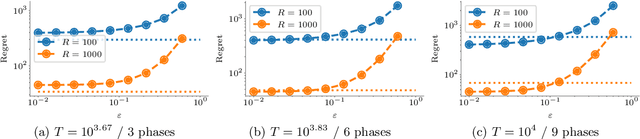
Web crawling is the problem of keeping a cache of webpages fresh, i.e., having the most recent copy available when a page is requested. This problem is usually coupled with the natural restriction that the bandwidth available to the web crawler is limited. The corresponding optimization problem was solved optimally by Azar et al. [2018] under the assumption that, for each webpage, both the elapsed time between two changes and the elapsed time between two requests follow a Poisson distribution with known parameters. In this paper, we study the same control problem but under the assumption that the change rates are unknown a priori, and thus we need to estimate them in an online fashion using only partial observations (i.e., single-bit signals indicating whether the page has changed since the last refresh). As a point of departure, we characterise the conditions under which one can solve the problem with such partial observability. Next, we propose a practical estimator and compute confidence intervals for it in terms of the elapsed time between the observations. Finally, we show that the explore-and-commit algorithm achieves an $\mathcal{O}(\sqrt{T})$ regret with a carefully chosen exploration horizon. Our simulation study shows that our online policy scales well and achieves close to optimal performance for a wide range of the parameters.

On-line PCA with Optimal Regrets

We carefully investigate the on-line version of PCA, where in each trial a learning algorithm plays a k-dimensional subspace, and suffers the compression loss on the next instance when projected into the chosen subspace. In this setting, we analyze two popular on-line algorithms, Gradient Descent (GD) and Exponentiated Gradient (EG). We show that both algorithms are essentially optimal in the worst-case. This comes as a surprise, since EG is known to perform sub-optimally when the instances are sparse. This different behavior of EG for PCA is mainly related to the non-negativity of the loss in this case, which makes the PCA setting qualitatively different from other settings studied in the literature. Furthermore, we show that when considering regret bounds as function of a loss budget, EG remains optimal and strictly outperforms GD. Next, we study the extension of the PCA setting, in which the Nature is allowed to play with dense instances, which are positive matrices with bounded largest eigenvalue. Again we can show that EG is optimal and strictly better than GD in this setting.

Horizon-Independent Optimal Prediction with Log-Loss in Exponential Families

We study online learning under logarithmic loss with regular parametric models. Hedayati and Bartlett (2012b) showed that a Bayesian prediction strategy with Jeffreys prior and sequential normalized maximum likelihood (SNML) coincide and are optimal if and only if the latter is exchangeable, and if and only if the optimal strategy can be calculated without knowing the time horizon in advance. They put forward the question what families have exchangeable SNML strategies. This paper fully answers this open problem for one-dimensional exponential families. The exchangeability can happen only for three classes of natural exponential family distributions, namely the Gaussian, Gamma, and the Tweedie exponential family of order 3/2. Keywords: SNML Exchangeability, Exponential Family, Online Learning, Logarithmic Loss, Bayesian Strategy, Jeffreys Prior, Fisher Information1

Consistent Multilabel Ranking through Univariate Losses

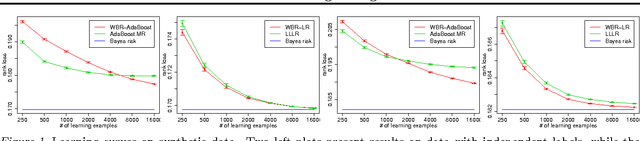
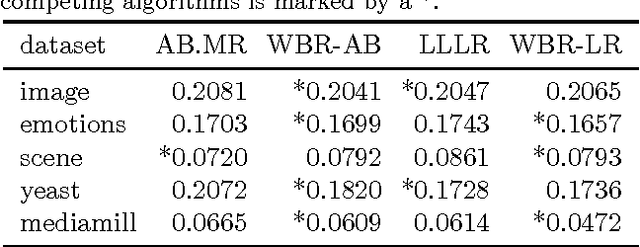
We consider the problem of rank loss minimization in the setting of multilabel classification, which is usually tackled by means of convex surrogate losses defined on pairs of labels. Very recently, this approach was put into question by a negative result showing that commonly used pairwise surrogate losses, such as exponential and logistic losses, are inconsistent. In this paper, we show a positive result which is arguably surprising in light of the previous one: the simpler univariate variants of exponential and logistic surrogates (i.e., defined on single labels) are consistent for rank loss minimization. Instead of directly proving convergence, we give a much stronger result by deriving regret bounds and convergence rates. The proposed losses suggest efficient and scalable algorithms, which are tested experimentally.

Quantum learning: optimal classification of qubit states

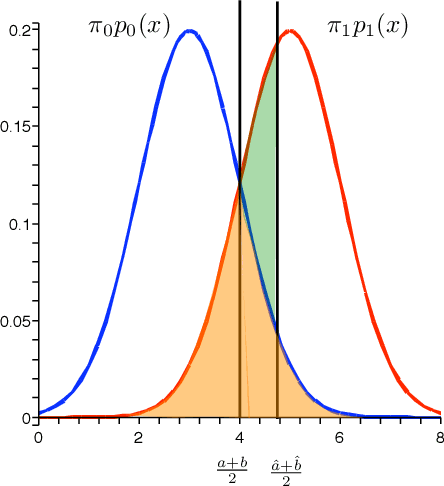
Pattern recognition is a central topic in Learning Theory with numerous applications such as voice and text recognition, image analysis, computer diagnosis. The statistical set-up in classification is the following: we are given an i.i.d. training set $(X_{1},Y_{1}),... (X_{n},Y_{n})$ where $X_{i}$ represents a feature and $Y_{i}\in \{0,1\}$ is a label attached to that feature. The underlying joint distribution of $(X,Y)$ is unknown, but we can learn about it from the training set and we aim at devising low error classifiers $f:X\to Y$ used to predict the label of new incoming features. Here we solve a quantum analogue of this problem, namely the classification of two arbitrary unknown qubit states. Given a number of `training' copies from each of the states, we would like to `learn' about them by performing a measurement on the training set. The outcome is then used to design mesurements for the classification of future systems with unknown labels. We find the asymptotically optimal classification strategy and show that typically, it performs strictly better than a plug-in strategy based on state estimation. The figure of merit is the excess risk which is the difference between the probability of error and the probability of error of the optimal measurement when the states are known, that is the Helstrom measurement. We show that the excess risk has rate $n^{-1}$ and compute the exact constant of the rate.