Robert Busa-Fekete
Dima
Nearly Optimal Sample Complexity for Learning with Label Proportions
May 08, 2025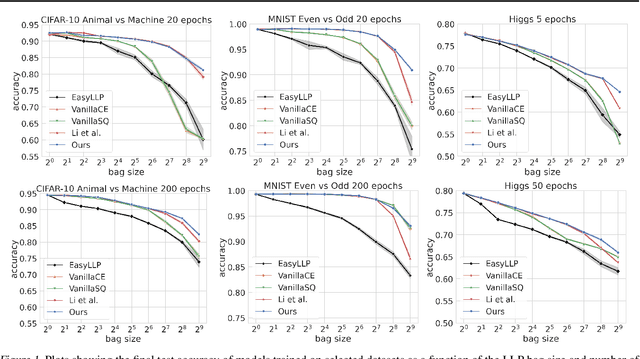
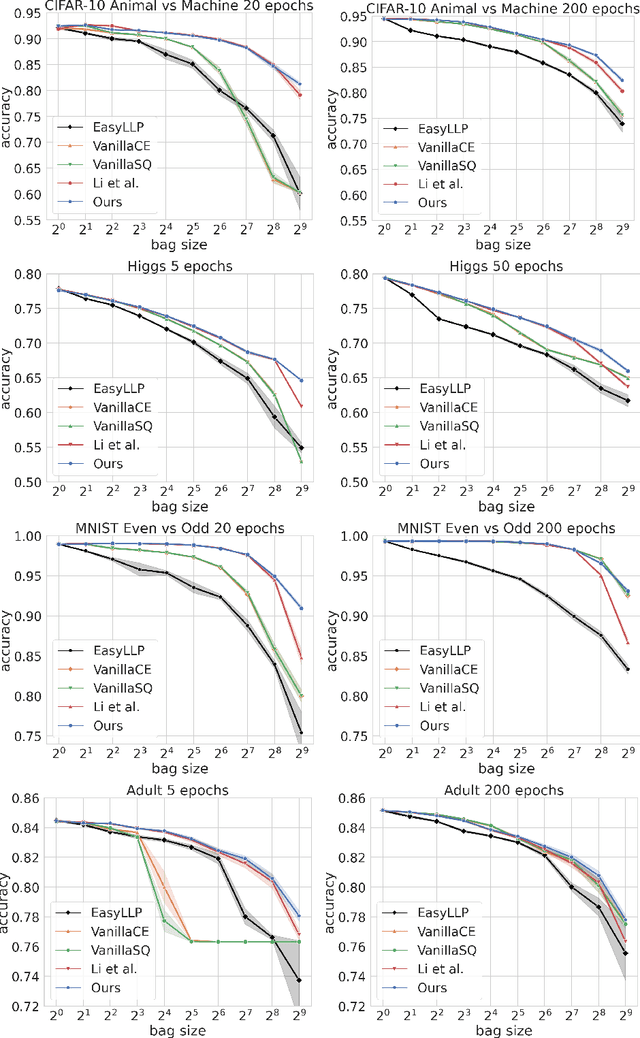
Abstract:We investigate Learning from Label Proportions (LLP), a partial information setting where examples in a training set are grouped into bags, and only aggregate label values in each bag are available. Despite the partial observability, the goal is still to achieve small regret at the level of individual examples. We give results on the sample complexity of LLP under square loss, showing that our sample complexity is essentially optimal. From an algorithmic viewpoint, we rely on carefully designed variants of Empirical Risk Minimization, and Stochastic Gradient Descent algorithms, combined with ad hoc variance reduction techniques. On one hand, our theoretical results improve in important ways on the existing literature on LLP, specifically in the way the sample complexity depends on the bag size. On the other hand, we validate our algorithmic solutions on several datasets, demonstrating improved empirical performance (better accuracy for less samples) against recent baselines.
Near-optimal algorithms for private estimation and sequential testing of collision probability
Apr 18, 2025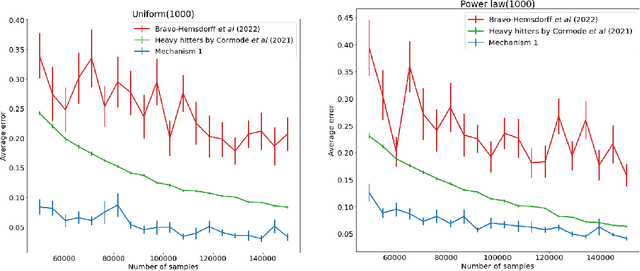
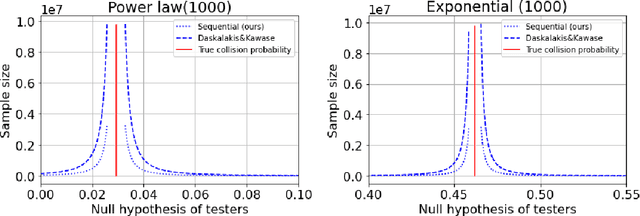
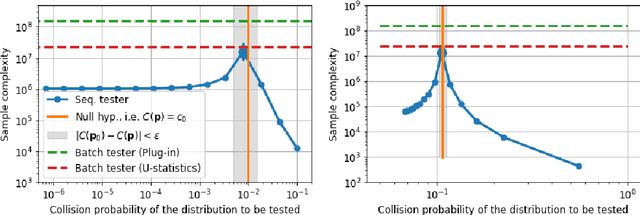
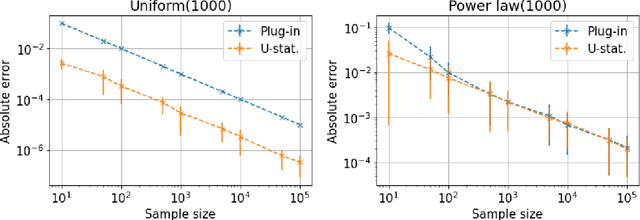
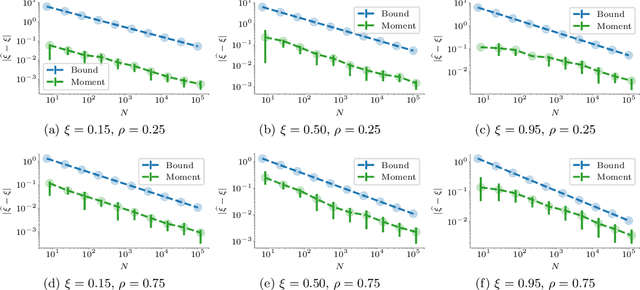
Abstract:We present new algorithms for estimating and testing \emph{collision probability}, a fundamental measure of the spread of a discrete distribution that is widely used in many scientific fields. We describe an algorithm that satisfies $(\alpha, \beta)$-local differential privacy and estimates collision probability with error at most $\epsilon$ using $\tilde{O}\left(\frac{\log(1/\beta)}{\alpha^2 \epsilon^2}\right)$ samples for $\alpha \le 1$, which improves over previous work by a factor of $\frac{1}{\alpha^2}$. We also present a sequential testing algorithm for collision probability, which can distinguish between collision probability values that are separated by $\epsilon$ using $\tilde{O}(\frac{1}{\epsilon^2})$ samples, even when $\epsilon$ is unknown. Our algorithms have nearly the optimal sample complexity, and in experiments we show that they require significantly fewer samples than previous methods.
Gemma 3 Technical Report
Mar 25, 2025Abstract:We introduce Gemma 3, a multimodal addition to the Gemma family of lightweight open models, ranging in scale from 1 to 27 billion parameters. This version introduces vision understanding abilities, a wider coverage of languages and longer context - at least 128K tokens. We also change the architecture of the model to reduce the KV-cache memory that tends to explode with long context. This is achieved by increasing the ratio of local to global attention layers, and keeping the span on local attention short. The Gemma 3 models are trained with distillation and achieve superior performance to Gemma 2 for both pre-trained and instruction finetuned versions. In particular, our novel post-training recipe significantly improves the math, chat, instruction-following and multilingual abilities, making Gemma3-4B-IT competitive with Gemma2-27B-IT and Gemma3-27B-IT comparable to Gemini-1.5-Pro across benchmarks. We release all our models to the community.
Probabilistic Label Trees for Extreme Multi-label Classification
Sep 23, 2020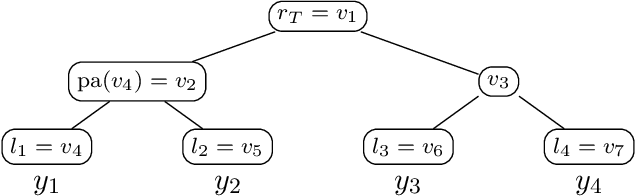

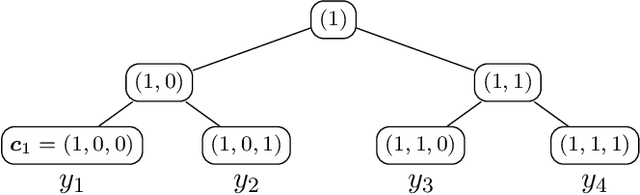
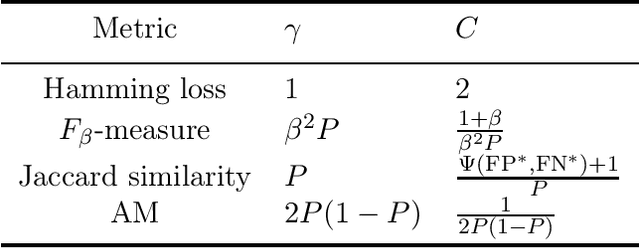
Abstract:Extreme multi-label classification (XMLC) is a learning task of tagging instances with a small subset of relevant labels chosen from an extremely large pool of possible labels. Problems of this scale can be efficiently handled by organizing labels as a tree, like in hierarchical softmax used for multi-class problems. In this paper, we thoroughly investigate probabilistic label trees (PLTs) which can be treated as a generalization of hierarchical softmax for multi-label problems. We first introduce the PLT model and discuss training and inference procedures and their computational costs. Next, we prove the consistency of PLTs for a wide spectrum of performance metrics. To this end, we upperbound their regret by a function of surrogate-loss regrets of node classifiers. Furthermore, we consider a problem of training PLTs in a fully online setting, without any prior knowledge of training instances, their features, or labels. In this case, both node classifiers and the tree structure are trained online. We prove a specific equivalence between the fully online algorithm and an algorithm with a tree structure given in advance. Finally, we discuss several implementations of PLTs and introduce a new one, napkinXC, which we empirically evaluate and compare with state-of-the-art algorithms.
On the computational complexity of the probabilistic label tree algorithms
Jun 01, 2019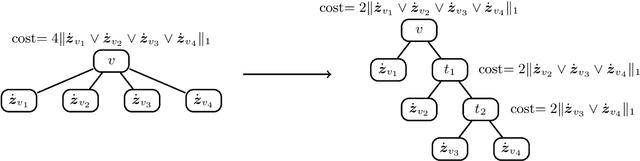
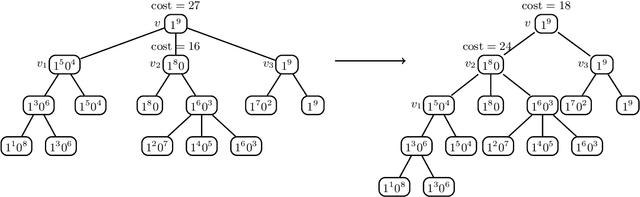


Abstract:Label tree-based algorithms are widely used to tackle multi-class and multi-label problems with a large number of labels. We focus on a particular subclass of these algorithms that use probabilistic classifiers in the tree nodes. Examples of such algorithms are hierarchical softmax (HSM), designed for multi-class classification, and probabilistic label trees (PLTs) that generalize HSM to multi-label problems. If the tree structure is given, learning of PLT can be solved with provable regret guaranties [Wydmuch et.al. 2018]. However, to find a tree structure that results in a PLT with a low training and prediction computational costs as well as low statistical error seems to be a very challenging problem, not well-understood yet. In this paper, we address the problem of finding a tree structure that has low computational cost. First, we show that finding a tree with optimal training cost is NP-complete, nevertheless there are some tractable special cases with either perfect approximation or exact solution that can be obtained in linear time in terms of the number of labels $m$. For the general case, we obtain $O(\log m)$ approximation in linear time too. Moreover, we prove an upper bound on the expected prediction cost expressed in terms of the expected training cost. We also show that under additional assumptions the prediction cost of a PLT is $O(\log m)$.
Learning to Crawl
May 29, 2019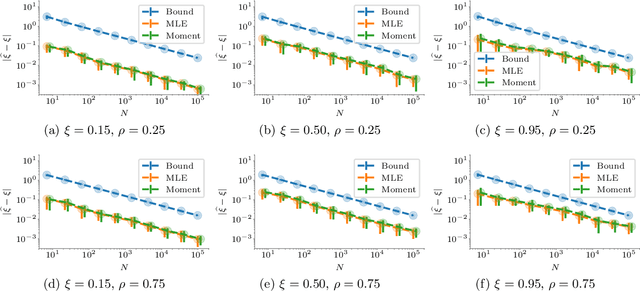
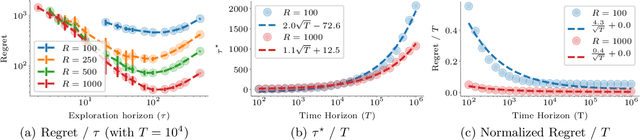
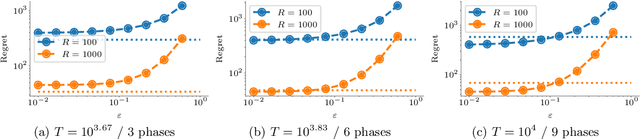
Abstract:Web crawling is the problem of keeping a cache of webpages fresh, i.e., having the most recent copy available when a page is requested. This problem is usually coupled with the natural restriction that the bandwidth available to the web crawler is limited. The corresponding optimization problem was solved optimally by Azar et al. [2018] under the assumption that, for each webpage, both the elapsed time between two changes and the elapsed time between two requests follow a Poisson distribution with known parameters. In this paper, we study the same control problem but under the assumption that the change rates are unknown a priori, and thus we need to estimate them in an online fashion using only partial observations (i.e., single-bit signals indicating whether the page has changed since the last refresh). As a point of departure, we characterise the conditions under which one can solve the problem with such partial observability. Next, we propose a practical estimator and compute confidence intervals for it in terms of the elapsed time between the observations. Finally, we show that the explore-and-commit algorithm achieves an $\mathcal{O}(\sqrt{T})$ regret with a carefully chosen exploration horizon. Our simulation study shows that our online policy scales well and achieves close to optimal performance for a wide range of the parameters.
Distributed Stochastic Optimization via Adaptive SGD
Oct 29, 2018
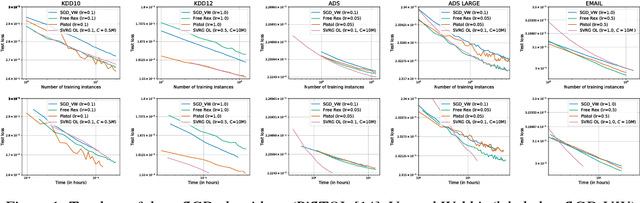

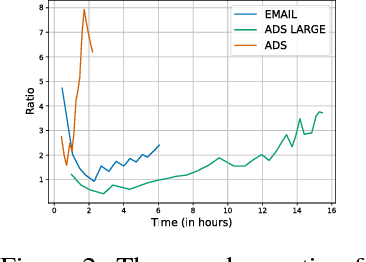
Abstract:Stochastic convex optimization algorithms are the most popular way to train machine learning models on large-scale data. Scaling up the training process of these models is crucial, but the most popular algorithm, Stochastic Gradient Descent (SGD), is a serial method that is surprisingly hard to parallelize. In this paper, we propose an efficient distributed stochastic optimization method by combining adaptivity with variance reduction techniques. Our analysis yields a linear speedup in the number of machines, constant memory footprint, and only a logarithmic number of communication rounds. Critically, our approach is a black-box reduction that parallelizes any serial online learning algorithm, streamlining prior analysis and allowing us to leverage the significant progress that has been made in designing adaptive algorithms. In particular, we achieve optimal convergence rates without any prior knowledge of smoothness parameters, yielding a more robust algorithm that reduces the need for hyperparameter tuning. We implement our algorithm in the Spark distributed framework and exhibit dramatic performance gains on large-scale logistic regression problems.
Preference-based Online Learning with Dueling Bandits: A Survey
Jul 30, 2018
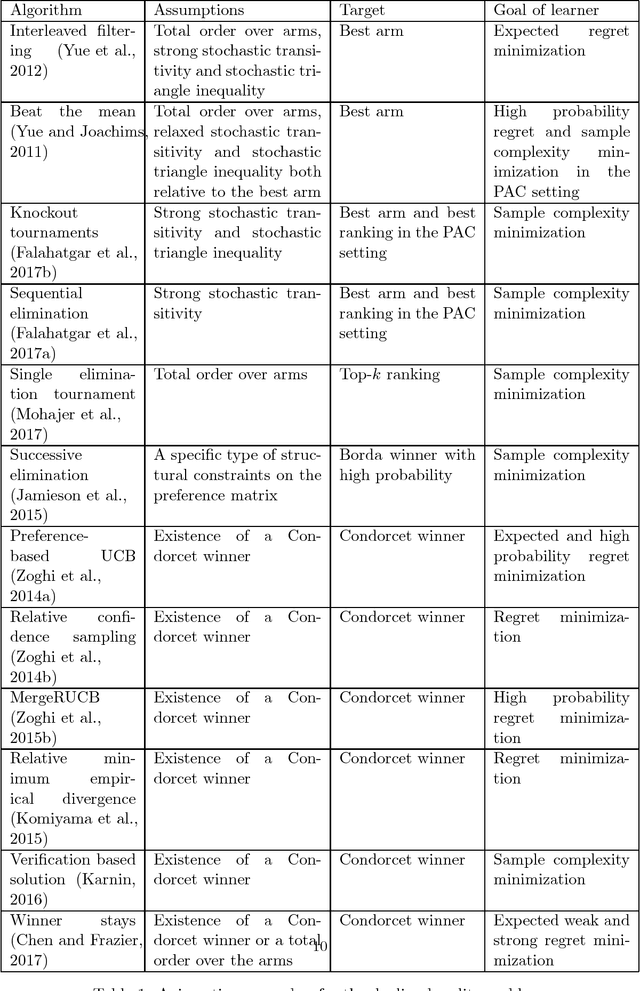
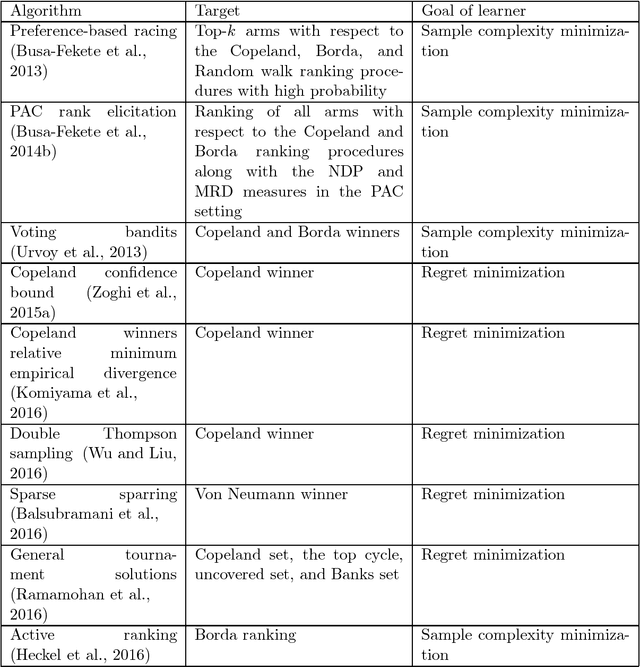
Abstract:In machine learning, the notion of multi-armed bandits refers to a class of online learning problems, in which an agent is supposed to simultaneously explore and exploit a given set of choice alternatives in the course of a sequential decision process. In the standard setting, the agent learns from stochastic feedback in the form of real-valued rewards. In many applications, however, numerical reward signals are not readily available -- instead, only weaker information is provided, in particular relative preferences in the form of qualitative comparisons between pairs of alternatives. This observation has motivated the study of variants of the multi-armed bandit problem, in which more general representations are used both for the type of feedback to learn from and the target of prediction. The aim of this paper is to provide a survey of the state of the art in this field, referred to as preference-based multi-armed bandits or dueling bandits. To this end, we provide an overview of problems that have been considered in the literature as well as methods for tackling them. Our taxonomy is mainly based on the assumptions made by these methods about the data-generating process and, related to this, the properties of the preference-based feedback.
Multi-objective Bandits: Optimizing the Generalized Gini Index
Jun 15, 2017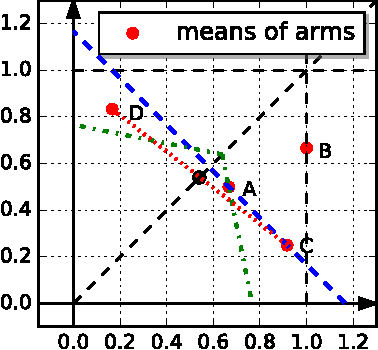
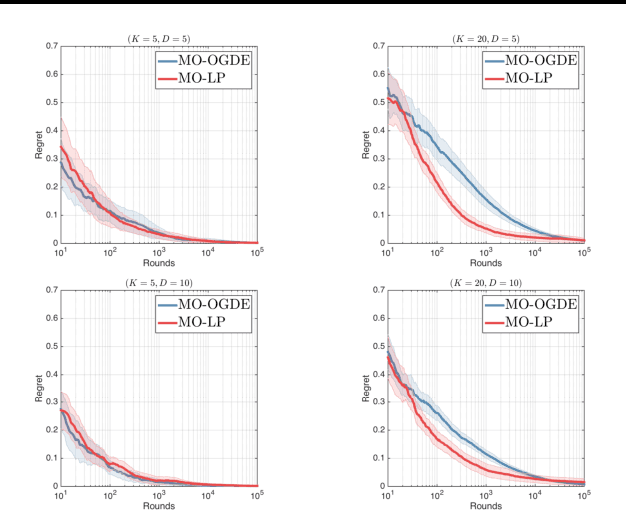
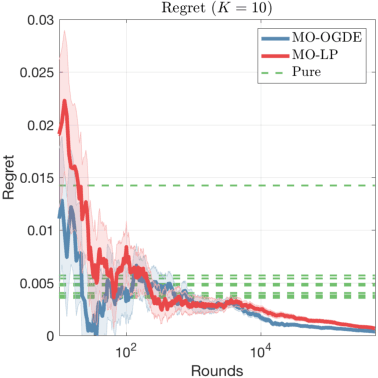
Abstract:We study the multi-armed bandit (MAB) problem where the agent receives a vectorial feedback that encodes many possibly competing objectives to be optimized. The goal of the agent is to find a policy, which can optimize these objectives simultaneously in a fair way. This multi-objective online optimization problem is formalized by using the Generalized Gini Index (GGI) aggregation function. We propose an online gradient descent algorithm which exploits the convexity of the GGI aggregation function, and controls the exploration in a careful way achieving a distribution-free regret $\tilde{\bigO} (T^{-1/2} )$ with high probability. We test our algorithm on synthetic data as well as on an electric battery control problem where the goal is to trade off the use of the different cells of a battery in order to balance their respective degradation rates.
Fast classification using sparse decision DAGs
Jun 27, 2012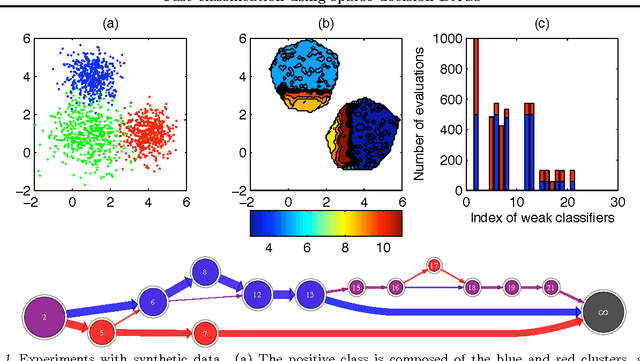
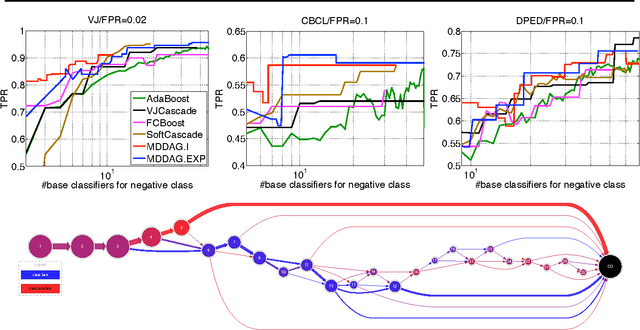
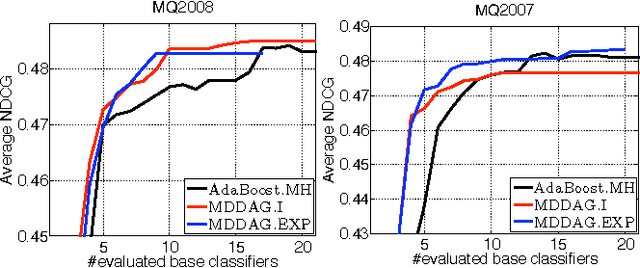
Abstract:In this paper we propose an algorithm that builds sparse decision DAGs (directed acyclic graphs) from a list of base classifiers provided by an external learning method such as AdaBoost. The basic idea is to cast the DAG design task as a Markov decision process. Each instance can decide to use or to skip each base classifier, based on the current state of the classifier being built. The result is a sparse decision DAG where the base classifiers are selected in a data-dependent way. The method has a single hyperparameter with a clear semantics of controlling the accuracy/speed trade-off. The algorithm is competitive with state-of-the-art cascade detectors on three object-detection benchmarks, and it clearly outperforms them when there is a small number of base classifiers. Unlike cascades, it is also readily applicable for multi-class classification. Using the multi-class setup, we show on a benchmark web page ranking data set that we can significantly improve the decision speed without harming the performance of the ranker.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge