On the computational complexity of the probabilistic label tree algorithms
Paper and Code
Jun 01, 2019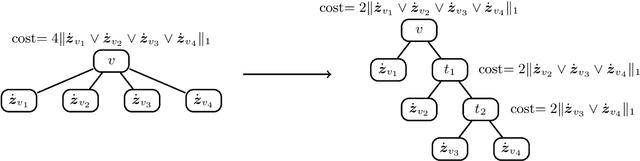
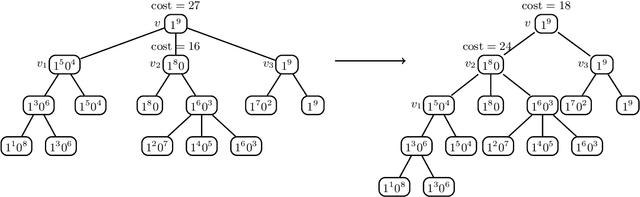


Label tree-based algorithms are widely used to tackle multi-class and multi-label problems with a large number of labels. We focus on a particular subclass of these algorithms that use probabilistic classifiers in the tree nodes. Examples of such algorithms are hierarchical softmax (HSM), designed for multi-class classification, and probabilistic label trees (PLTs) that generalize HSM to multi-label problems. If the tree structure is given, learning of PLT can be solved with provable regret guaranties [Wydmuch et.al. 2018]. However, to find a tree structure that results in a PLT with a low training and prediction computational costs as well as low statistical error seems to be a very challenging problem, not well-understood yet. In this paper, we address the problem of finding a tree structure that has low computational cost. First, we show that finding a tree with optimal training cost is NP-complete, nevertheless there are some tractable special cases with either perfect approximation or exact solution that can be obtained in linear time in terms of the number of labels $m$. For the general case, we obtain $O(\log m)$ approximation in linear time too. Moreover, we prove an upper bound on the expected prediction cost expressed in terms of the expected training cost. We also show that under additional assumptions the prediction cost of a PLT is $O(\log m)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge