Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence

This is the Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence, which was held on Catalina Island, CA, July 8 - 11 2010.

Horizon-Independent Optimal Prediction with Log-Loss in Exponential Families

We study online learning under logarithmic loss with regular parametric models. Hedayati and Bartlett (2012b) showed that a Bayesian prediction strategy with Jeffreys prior and sequential normalized maximum likelihood (SNML) coincide and are optimal if and only if the latter is exchangeable, and if and only if the optimal strategy can be calculated without knowing the time horizon in advance. They put forward the question what families have exchangeable SNML strategies. This paper fully answers this open problem for one-dimensional exponential families. The exchangeability can happen only for three classes of natural exponential family distributions, namely the Gaussian, Gamma, and the Tweedie exponential family of order 3/2. Keywords: SNML Exchangeability, Exponential Family, Online Learning, Logarithmic Loss, Bayesian Strategy, Jeffreys Prior, Fisher Information1

Entropy Concentration and the Empirical Coding Game

We give a characterization of Maximum Entropy/Minimum Relative Entropy inference by providing two `strong entropy concentration' theorems. These theorems unify and generalize Jaynes' `concentration phenomenon' and Van Campenhout and Cover's `conditional limit theorem'. The theorems characterize exactly in what sense a prior distribution Q conditioned on a given constraint, and the distribution P, minimizing the relative entropy D(P ||Q) over all distributions satisfying the constraint, are `close' to each other. We then apply our theorems to establish the relationship between entropy concentration and a game-theoretic characterization of Maximum Entropy Inference due to Topsoe and others.

Catching Up Faster by Switching Sooner: A Prequential Solution to the AIC-BIC Dilemma

Bayesian model averaging, model selection and its approximations such as BIC are generally statistically consistent, but sometimes achieve slower rates og convergence than other methods such as AIC and leave-one-out cross-validation. On the other hand, these other methods can br inconsistent. We identify the "catch-up phenomenon" as a novel explanation for the slow convergence of Bayesian methods. Based on this analysis we define the switch distribution, a modification of the Bayesian marginal distribution. We show that, under broad conditions,model selection and prediction based on the switch distribution is both consistent and achieves optimal convergence rates, thereby resolving the AIC-BIC dilemma. The method is practical; we give an efficient implementation. The switch distribution has a data compression interpretation, and can thus be viewed as a "prequential" or MDL method; yet it is different from the MDL methods that are usually considered in the literature. We compare the switch distribution to Bayes factor model selection and leave-one-out cross-validation.

Asymptotic Log-loss of Prequential Maximum Likelihood Codes

We analyze the Dawid-Rissanen prequential maximum likelihood codes relative to one-parameter exponential family models M. If data are i.i.d. according to an (essentially) arbitrary P, then the redundancy grows at rate c/2 ln n. We show that c=v1/v2, where v1 is the variance of P, and v2 is the variance of the distribution m* in M that is closest to P in KL divergence. This shows that prequential codes behave quite differently from other important universal codes such as the 2-part MDL, Shtarkov and Bayes codes, for which c=1. This behavior is undesirable in an MDL model selection setting.

An Empirical Study of MDL Model Selection with Infinite Parametric Complexity

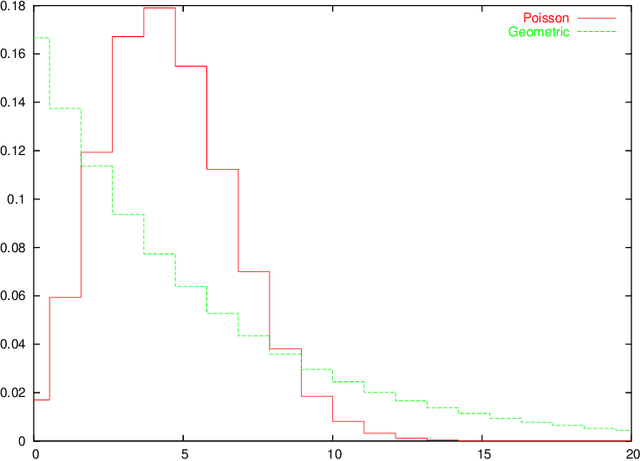
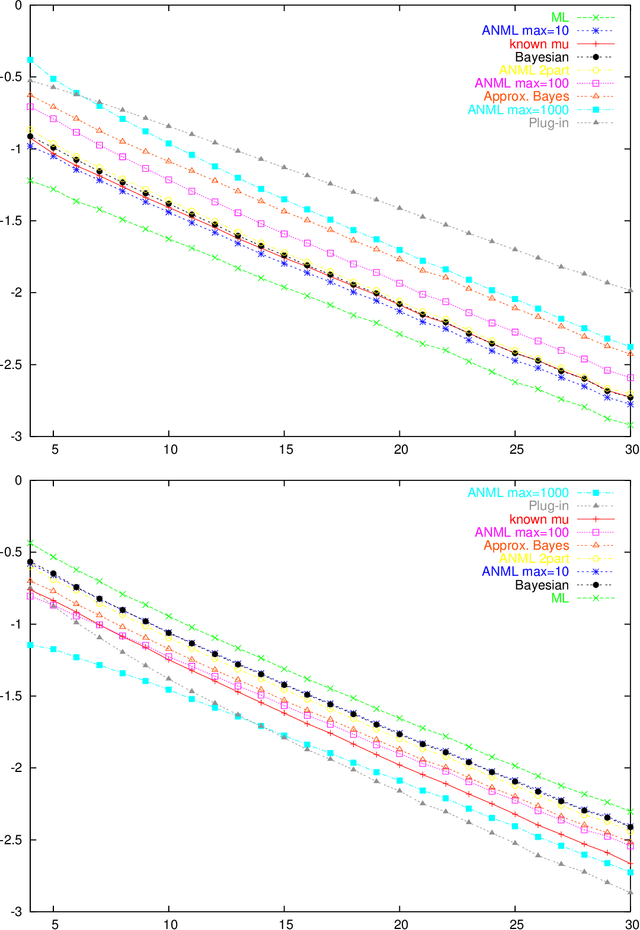
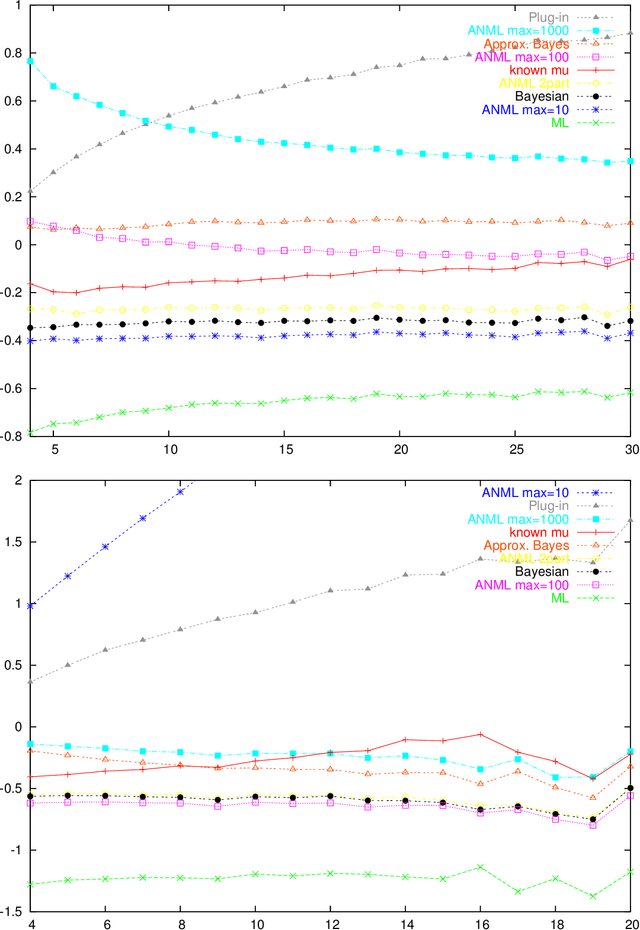
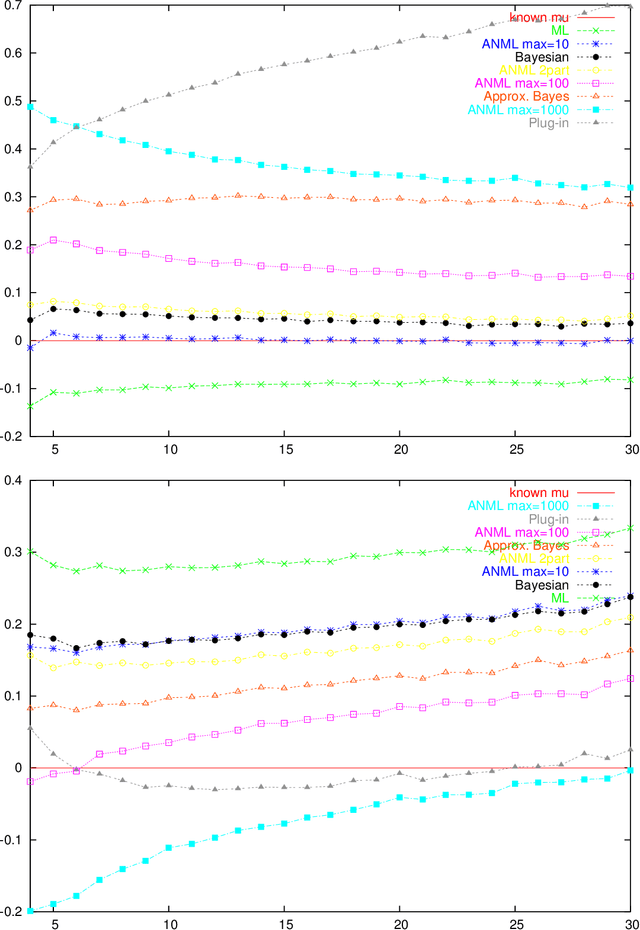
Parametric complexity is a central concept in MDL model selection. In practice it often turns out to be infinite, even for quite simple models such as the Poisson and Geometric families. In such cases, MDL model selection as based on NML and Bayesian inference based on Jeffreys' prior can not be used. Several ways to resolve this problem have been proposed. We conduct experiments to compare and evaluate their behaviour on small sample sizes. We find interestingly poor behaviour for the plug-in predictive code; a restricted NML model performs quite well but it is questionable if the results validate its theoretical motivation. The Bayesian model with the improper Jeffreys' prior is the most dependable.

Suboptimal behaviour of Bayes and MDL in classification under misspecification

We show that forms of Bayesian and MDL inference that are often applied to classification problems can be *inconsistent*. This means there exists a learning problem such that for all amounts of data the generalization errors of the MDL classifier and the Bayes classifier relative to the Bayesian posterior both remain bounded away from the smallest achievable generalization error.

A tutorial introduction to the minimum description length principle

This tutorial provides an overview of and introduction to Rissanen's Minimum Description Length (MDL) Principle. The first chapter provides a conceptual, entirely non-technical introduction to the subject. It serves as a basis for the technical introduction given in the second chapter, in which all the ideas of the first chapter are made mathematically precise. The main ideas are discussed in great conceptual and technical detail. This tutorial is an extended version of the first two chapters of the collection "Advances in Minimum Description Length: Theory and Application" (edited by P.Grunwald, I.J. Myung and M. Pitt, to be published by the MIT Press, Spring 2005).