Jiazhong Nie
Learning to Organize Knowledge and Answer Questions with N-Gram Machines
Jul 01, 2018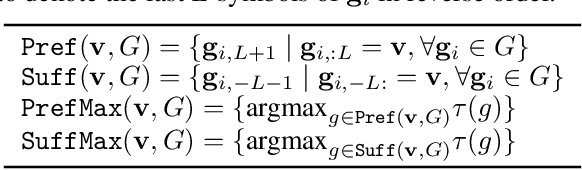

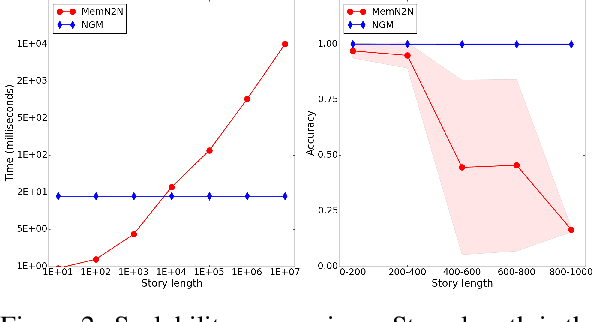
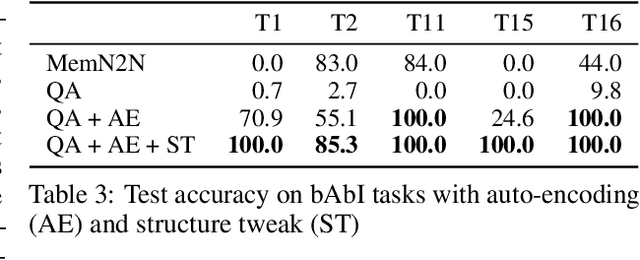
Abstract:Though deep neural networks have great success in natural language processing, they are limited at more knowledge intensive AI tasks, such as open-domain Question Answering (QA). Existing end-to-end deep QA models need to process the entire text after observing the question, and therefore their complexity in responding a question is linear in the text size. This is prohibitive for practical tasks such as QA from Wikipedia, a novel, or the Web. We propose to solve this scalability issue by using symbolic meaning representations, which can be indexed and retrieved efficiently with complexity that is independent of the text size. We apply our approach, called the N-Gram Machine (NGM), to three representative tasks. First as proof-of-concept, we demonstrate that NGM successfully solves the bAbI tasks of synthetic text. Second, we show that NGM scales to large corpus by experimenting on "life-long bAbI", a special version of bAbI that contains millions of sentences. Lastly on the WikiMovies dataset, we use NGM to induce latent structure (i.e. schema) and answer questions from natural language Wikipedia text, with only QA pairs as weak supervision.
On-line PCA with Optimal Regrets
May 09, 2014Abstract:We carefully investigate the on-line version of PCA, where in each trial a learning algorithm plays a k-dimensional subspace, and suffers the compression loss on the next instance when projected into the chosen subspace. In this setting, we analyze two popular on-line algorithms, Gradient Descent (GD) and Exponentiated Gradient (EG). We show that both algorithms are essentially optimal in the worst-case. This comes as a surprise, since EG is known to perform sub-optimally when the instances are sparse. This different behavior of EG for PCA is mainly related to the non-negativity of the loss in this case, which makes the PCA setting qualitatively different from other settings studied in the literature. Furthermore, we show that when considering regret bounds as function of a loss budget, EG remains optimal and strictly outperforms GD. Next, we study the extension of the PCA setting, in which the Nature is allowed to play with dense instances, which are positive matrices with bounded largest eigenvalue. Again we can show that EG is optimal and strictly better than GD in this setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge