Quantum learning: optimal classification of qubit states
Paper and Code
Apr 14, 2010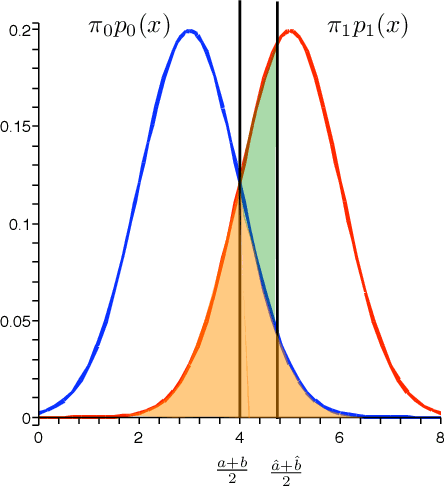

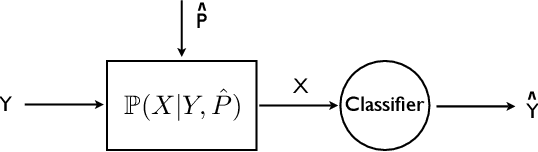
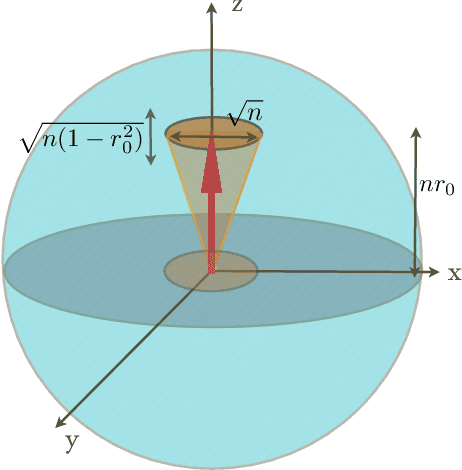
Pattern recognition is a central topic in Learning Theory with numerous applications such as voice and text recognition, image analysis, computer diagnosis. The statistical set-up in classification is the following: we are given an i.i.d. training set $(X_{1},Y_{1}),... (X_{n},Y_{n})$ where $X_{i}$ represents a feature and $Y_{i}\in \{0,1\}$ is a label attached to that feature. The underlying joint distribution of $(X,Y)$ is unknown, but we can learn about it from the training set and we aim at devising low error classifiers $f:X\to Y$ used to predict the label of new incoming features. Here we solve a quantum analogue of this problem, namely the classification of two arbitrary unknown qubit states. Given a number of `training' copies from each of the states, we would like to `learn' about them by performing a measurement on the training set. The outcome is then used to design mesurements for the classification of future systems with unknown labels. We find the asymptotically optimal classification strategy and show that typically, it performs strictly better than a plug-in strategy based on state estimation. The figure of merit is the excess risk which is the difference between the probability of error and the probability of error of the optimal measurement when the states are known, that is the Helstrom measurement. We show that the excess risk has rate $n^{-1}$ and compute the exact constant of the rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge