Hyperdimensional computing: a fast, robust and interpretable paradigm for biological data

Advances in bioinformatics are primarily due to new algorithms for processing diverse biological data sources. While sophisticated alignment algorithms have been pivotal in analyzing biological sequences, deep learning has substantially transformed bioinformatics, addressing sequence, structure, and functional analyses. However, these methods are incredibly data-hungry, compute-intensive and hard to interpret. Hyperdimensional computing (HDC) has recently emerged as an intriguing alternative. The key idea is that random vectors of high dimensionality can represent concepts such as sequence identity or phylogeny. These vectors can then be combined using simple operators for learning, reasoning or querying by exploiting the peculiar properties of high-dimensional spaces. Our work reviews and explores the potential of HDC for bioinformatics, emphasizing its efficiency, interpretability, and adeptness in handling multimodal and structured data. HDC holds a lot of potential for various omics data searching, biosignal analysis and health applications.

The Hyperdimensional Transform for Distributional Modelling, Regression and Classification

Hyperdimensional computing (HDC) is an increasingly popular computing paradigm with immense potential for future intelligent applications. Although the main ideas already took form in the 1990s, HDC recently gained significant attention, especially in the field of machine learning and data science. Next to efficiency, interoperability and explainability, HDC offers attractive properties for generalization as it can be seen as an attempt to combine connectionist ideas from neural networks with symbolic aspects. In recent work, we introduced the hyperdimensional transform, revealing deep theoretical foundations for representing functions and distributions as high-dimensional holographic vectors. Here, we present the power of the hyperdimensional transform to a broad data science audience. We use the hyperdimensional transform as a theoretical basis and provide insight into state-of-the-art HDC approaches for machine learning. We show how existing algorithms can be modified and how this transform can lead to a novel, well-founded toolbox. Next to the standard regression and classification tasks of machine learning, our discussion includes various aspects of statistical modelling, such as representation, learning and deconvolving distributions, sampling, Bayesian inference, and uncertainty estimation.

The Hyperdimensional Transform: a Holographic Representation of Functions

Integral transforms are invaluable mathematical tools to map functions into spaces where they are easier to characterize. We introduce the hyperdimensional transform as a new kind of integral transform. It converts square-integrable functions into noise-robust, holographic, high-dimensional representations called hyperdimensional vectors. The central idea is to approximate a function by a linear combination of random functions. We formally introduce a set of stochastic, orthogonal basis functions and define the hyperdimensional transform and its inverse. We discuss general transform-related properties such as its uniqueness, approximation properties of the inverse transform, and the representation of integrals and derivatives. The hyperdimensional transform offers a powerful, flexible framework that connects closely with other integral transforms, such as the Fourier, Laplace, and fuzzy transforms. Moreover, it provides theoretical foundations and new insights for the field of hyperdimensional computing, a computing paradigm that is rapidly gaining attention for efficient and explainable machine learning algorithms, with potential applications in statistical modelling and machine learning. In addition, we provide straightforward and easily understandable code, which can function as a tutorial and allows for the reproduction of the demonstrated examples, from computing the transform to solving differential equations.

A Comparative Study of Pairwise Learning Methods based on Kernel Ridge Regression

Many machine learning problems can be formulated as predicting labels for a pair of objects. Problems of that kind are often referred to as pairwise learning, dyadic prediction or network inference problems. During the last decade kernel methods have played a dominant role in pairwise learning. They still obtain a state-of-the-art predictive performance, but a theoretical analysis of their behavior has been underexplored in the machine learning literature. In this work we review and unify existing kernel-based algorithms that are commonly used in different pairwise learning settings, ranging from matrix filtering to zero-shot learning. To this end, we focus on closed-form efficient instantiations of Kronecker kernel ridge regression. We show that independent task kernel ridge regression, two-step kernel ridge regression and a linear matrix filter arise naturally as a special case of Kronecker kernel ridge regression, implying that all these methods implicitly minimize a squared loss. In addition, we analyze universality, consistency and spectral filtering properties. Our theoretical results provide valuable insights in assessing the advantages and limitations of existing pairwise learning methods.

Exact and efficient top-K inference for multi-target prediction by querying separable linear relational models

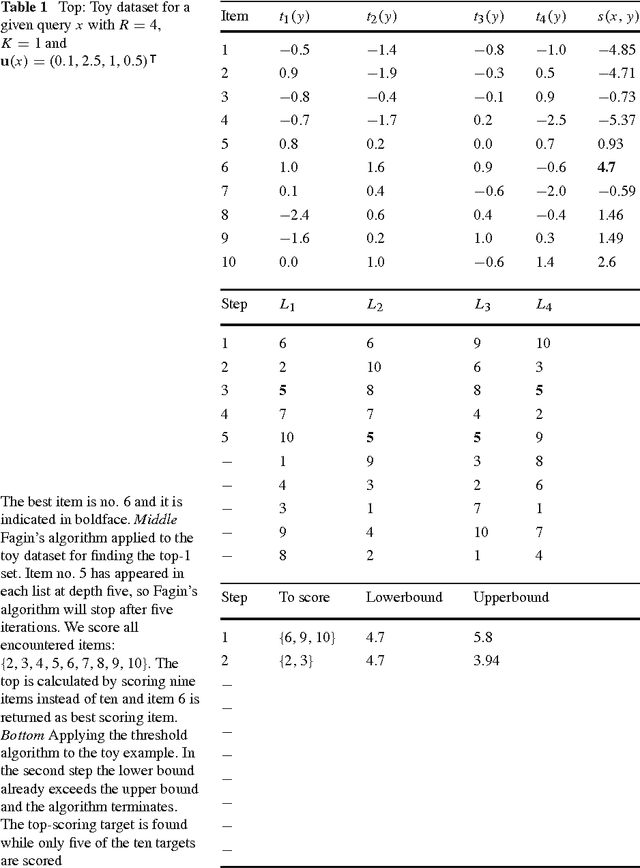
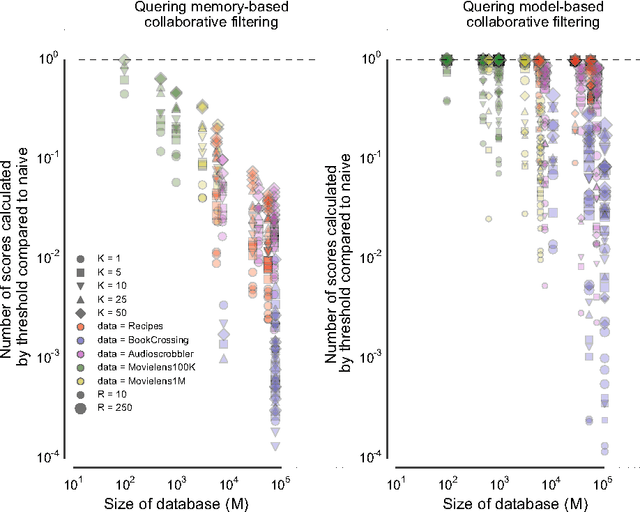
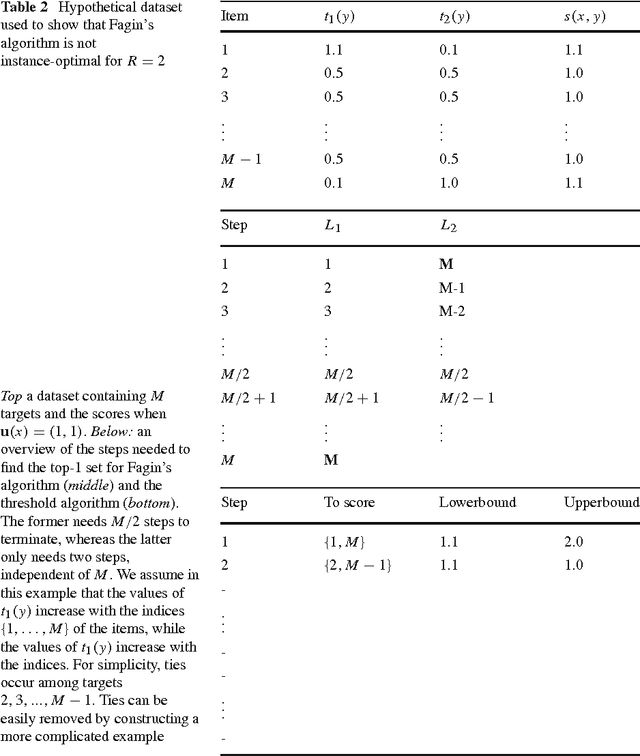
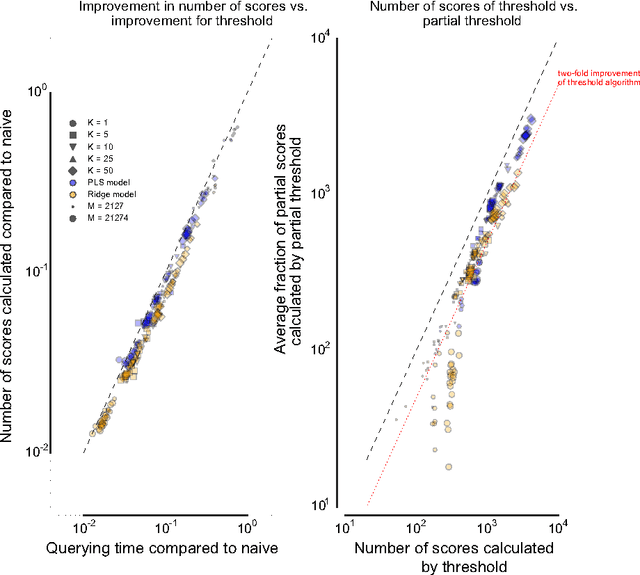
Many complex multi-target prediction problems that concern large target spaces are characterised by a need for efficient prediction strategies that avoid the computation of predictions for all targets explicitly. Examples of such problems emerge in several subfields of machine learning, such as collaborative filtering, multi-label classification, dyadic prediction and biological network inference. In this article we analyse efficient and exact algorithms for computing the top-$K$ predictions in the above problem settings, using a general class of models that we refer to as separable linear relational models. We show how to use those inference algorithms, which are modifications of well-known information retrieval methods, in a variety of machine learning settings. Furthermore, we study the possibility of scoring items incompletely, while still retaining an exact top-K retrieval. Experimental results in several application domains reveal that the so-called threshold algorithm is very scalable, performing often many orders of magnitude more efficiently than the naive approach.

Efficient Pairwise Learning Using Kernel Ridge Regression: an Exact Two-Step Method

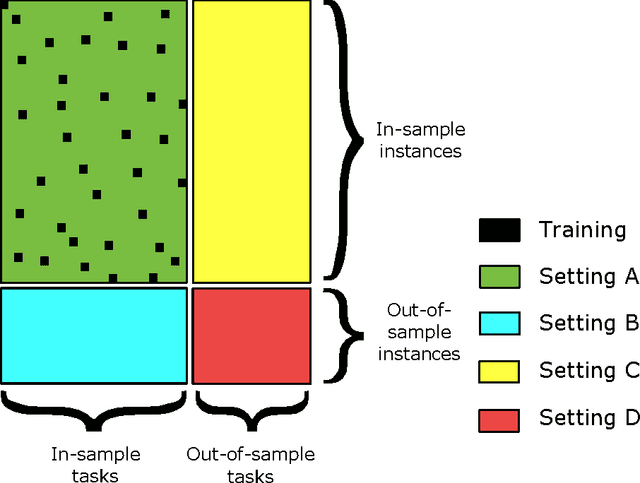
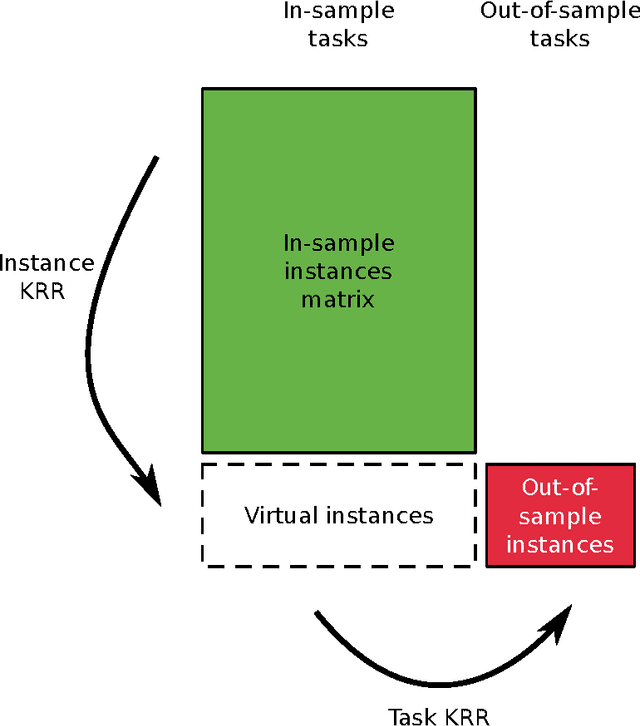
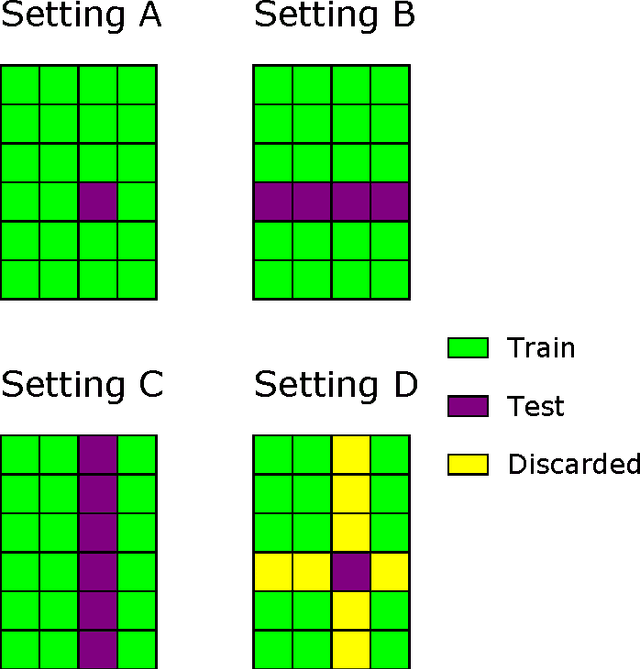
Pairwise learning or dyadic prediction concerns the prediction of properties for pairs of objects. It can be seen as an umbrella covering various machine learning problems such as matrix completion, collaborative filtering, multi-task learning, transfer learning, network prediction and zero-shot learning. In this work we analyze kernel-based methods for pairwise learning, with a particular focus on a recently-suggested two-step method. We show that this method offers an appealing alternative for commonly-applied Kronecker-based methods that model dyads by means of pairwise feature representations and pairwise kernels. In a series of theoretical results, we establish correspondences between the two types of methods in terms of linear algebra and spectral filtering, and we analyze their statistical consistency. In addition, the two-step method allows us to establish novel algorithmic shortcuts for efficient training and validation on very large datasets. Putting those properties together, we believe that this simple, yet powerful method can become a standard tool for many problems. Extensive experimental results for a range of practical settings are reported.

A two-step learning approach for solving full and almost full cold start problems in dyadic prediction

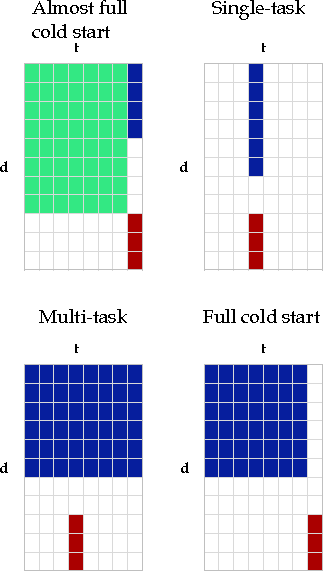
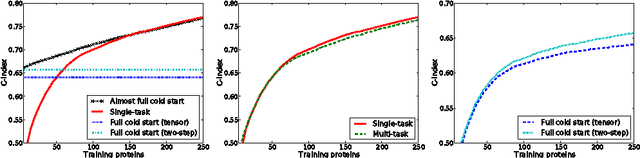
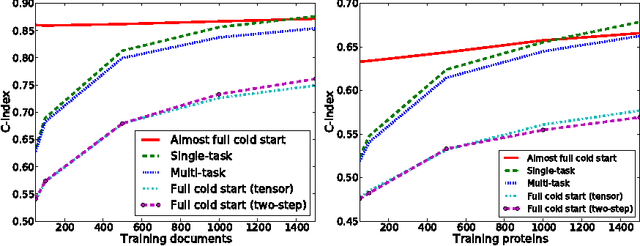
Dyadic prediction methods operate on pairs of objects (dyads), aiming to infer labels for out-of-sample dyads. We consider the full and almost full cold start problem in dyadic prediction, a setting that occurs when both objects in an out-of-sample dyad have not been observed during training, or if one of them has been observed, but very few times. A popular approach for addressing this problem is to train a model that makes predictions based on a pairwise feature representation of the dyads, or, in case of kernel methods, based on a tensor product pairwise kernel. As an alternative to such a kernel approach, we introduce a novel two-step learning algorithm that borrows ideas from the fields of pairwise learning and spectral filtering. We show theoretically that the two-step method is very closely related to the tensor product kernel approach, and experimentally that it yields a slightly better predictive performance. Moreover, unlike existing tensor product kernel methods, the two-step method allows closed-form solutions for training and parameter selection via cross-validation estimates both in the full and almost full cold start settings, making the approach much more efficient and straightforward to implement.

Identification of functionally related enzymes by learning-to-rank methods

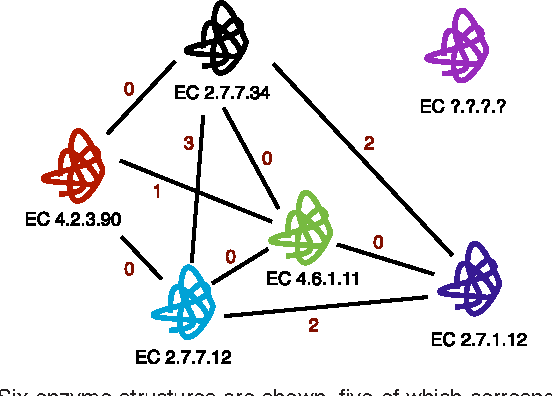
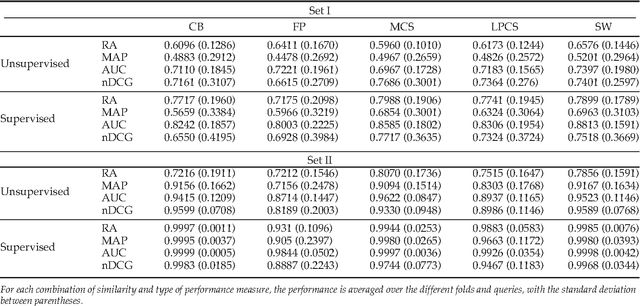
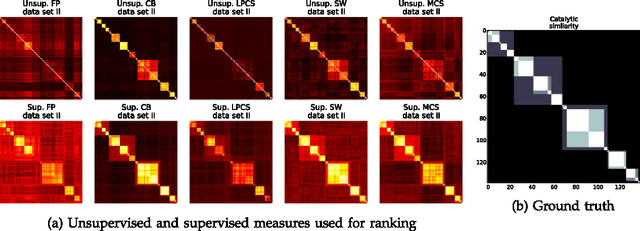
Enzyme sequences and structures are routinely used in the biological sciences as queries to search for functionally related enzymes in online databases. To this end, one usually departs from some notion of similarity, comparing two enzymes by looking for correspondences in their sequences, structures or surfaces. For a given query, the search operation results in a ranking of the enzymes in the database, from very similar to dissimilar enzymes, while information about the biological function of annotated database enzymes is ignored. In this work we show that rankings of that kind can be substantially improved by applying kernel-based learning algorithms. This approach enables the detection of statistical dependencies between similarities of the active cleft and the biological function of annotated enzymes. This is in contrast to search-based approaches, which do not take annotated training data into account. Similarity measures based on the active cleft are known to outperform sequence-based or structure-based measures under certain conditions. We consider the Enzyme Commission (EC) classification hierarchy for obtaining annotated enzymes during the training phase. The results of a set of sizeable experiments indicate a consistent and significant improvement for a set of similarity measures that exploit information about small cavities in the surface of enzymes.

Efficient Regularized Least-Squares Algorithms for Conditional Ranking on Relational Data

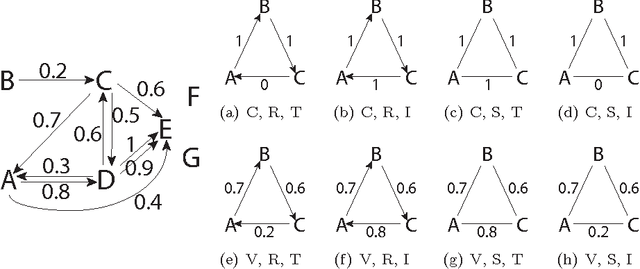
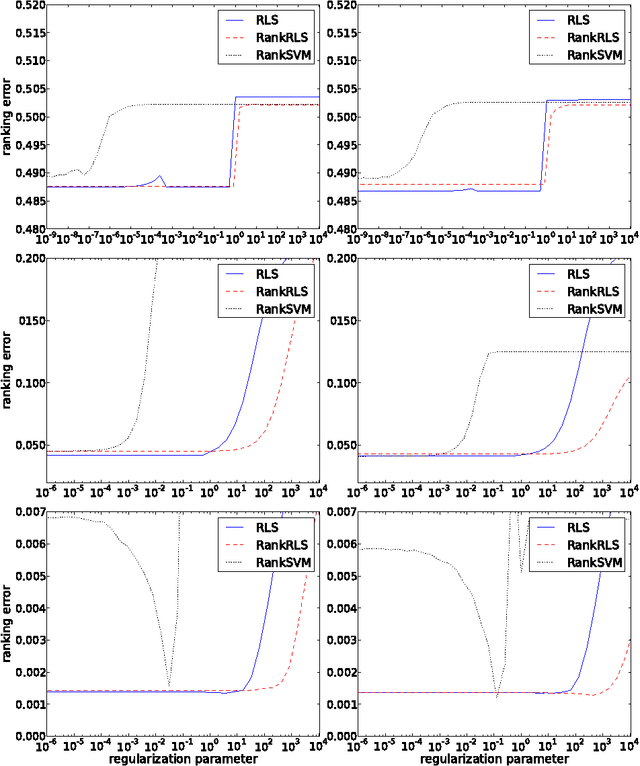
In domains like bioinformatics, information retrieval and social network analysis, one can find learning tasks where the goal consists of inferring a ranking of objects, conditioned on a particular target object. We present a general kernel framework for learning conditional rankings from various types of relational data, where rankings can be conditioned on unseen data objects. We propose efficient algorithms for conditional ranking by optimizing squared regression and ranking loss functions. We show theoretically, that learning with the ranking loss is likely to generalize better than with the regression loss. Further, we prove that symmetry or reciprocity properties of relations can be efficiently enforced in the learned models. Experiments on synthetic and real-world data illustrate that the proposed methods deliver state-of-the-art performance in terms of predictive power and computational efficiency. Moreover, we also show empirically that incorporating symmetry or reciprocity properties can improve the generalization performance.

A kernel-based framework for learning graded relations from data

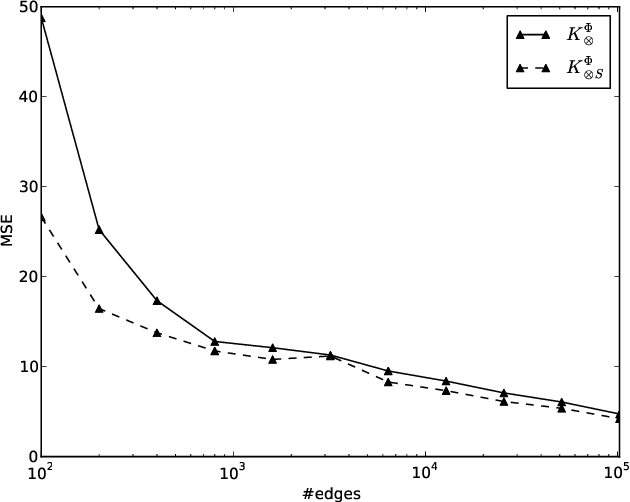
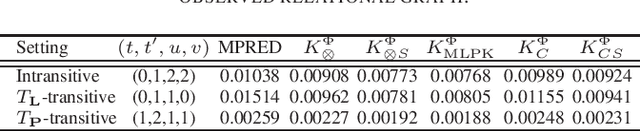
Driven by a large number of potential applications in areas like bioinformatics, information retrieval and social network analysis, the problem setting of inferring relations between pairs of data objects has recently been investigated quite intensively in the machine learning community. To this end, current approaches typically consider datasets containing crisp relations, so that standard classification methods can be adopted. However, relations between objects like similarities and preferences are often expressed in a graded manner in real-world applications. A general kernel-based framework for learning relations from data is introduced here. It extends existing approaches because both crisp and graded relations are considered, and it unifies existing approaches because different types of graded relations can be modeled, including symmetric and reciprocal relations. This framework establishes important links between recent developments in fuzzy set theory and machine learning. Its usefulness is demonstrated through various experiments on synthetic and real-world data.