A two-step learning approach for solving full and almost full cold start problems in dyadic prediction
Paper and Code
May 17, 2014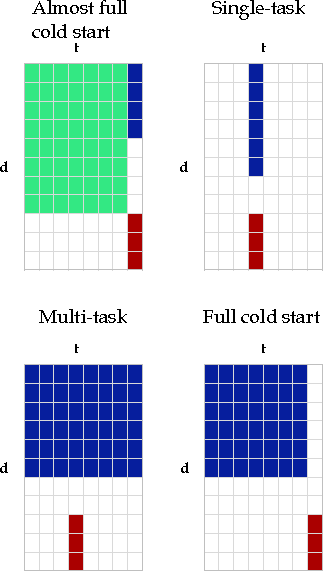
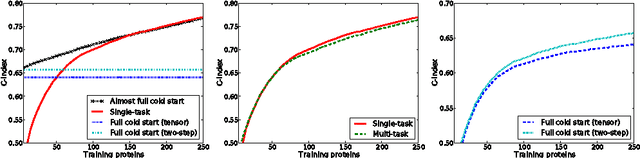
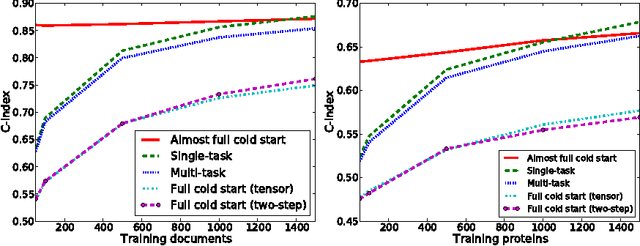
Dyadic prediction methods operate on pairs of objects (dyads), aiming to infer labels for out-of-sample dyads. We consider the full and almost full cold start problem in dyadic prediction, a setting that occurs when both objects in an out-of-sample dyad have not been observed during training, or if one of them has been observed, but very few times. A popular approach for addressing this problem is to train a model that makes predictions based on a pairwise feature representation of the dyads, or, in case of kernel methods, based on a tensor product pairwise kernel. As an alternative to such a kernel approach, we introduce a novel two-step learning algorithm that borrows ideas from the fields of pairwise learning and spectral filtering. We show theoretically that the two-step method is very closely related to the tensor product kernel approach, and experimentally that it yields a slightly better predictive performance. Moreover, unlike existing tensor product kernel methods, the two-step method allows closed-form solutions for training and parameter selection via cross-validation estimates both in the full and almost full cold start settings, making the approach much more efficient and straightforward to implement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge