Efficient Pairwise Learning Using Kernel Ridge Regression: an Exact Two-Step Method
Paper and Code
Jun 14, 2016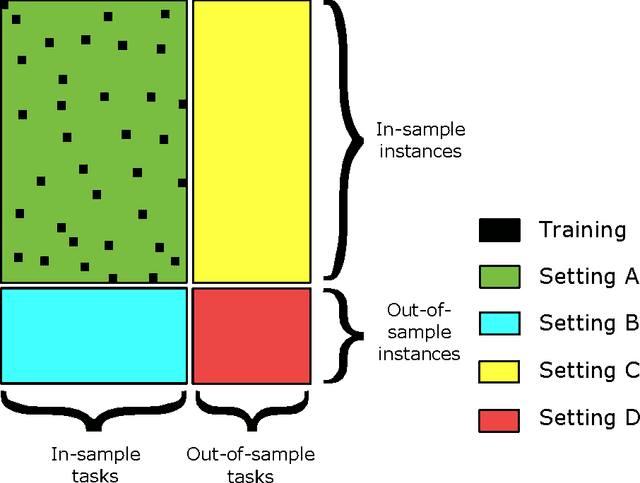
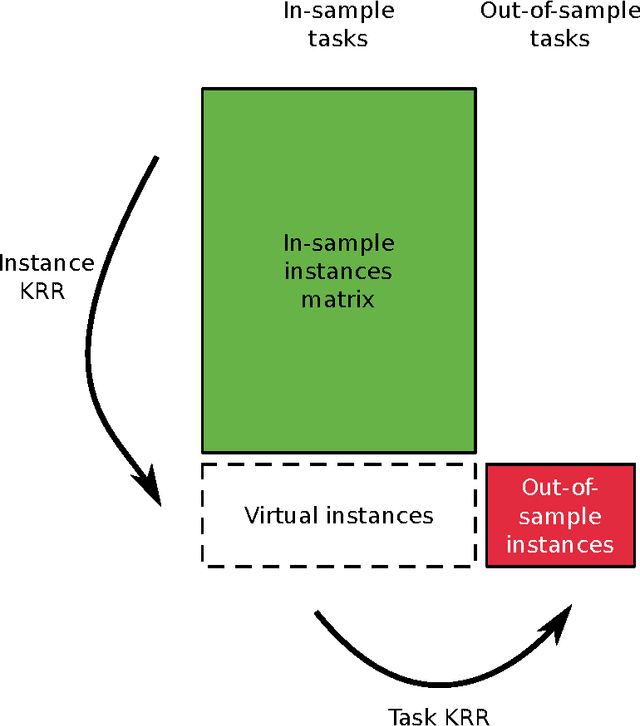

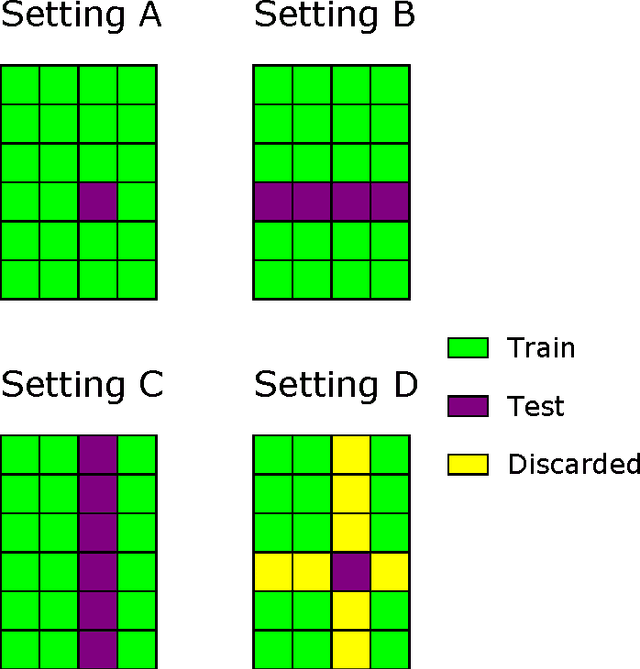
Pairwise learning or dyadic prediction concerns the prediction of properties for pairs of objects. It can be seen as an umbrella covering various machine learning problems such as matrix completion, collaborative filtering, multi-task learning, transfer learning, network prediction and zero-shot learning. In this work we analyze kernel-based methods for pairwise learning, with a particular focus on a recently-suggested two-step method. We show that this method offers an appealing alternative for commonly-applied Kronecker-based methods that model dyads by means of pairwise feature representations and pairwise kernels. In a series of theoretical results, we establish correspondences between the two types of methods in terms of linear algebra and spectral filtering, and we analyze their statistical consistency. In addition, the two-step method allows us to establish novel algorithmic shortcuts for efficient training and validation on very large datasets. Putting those properties together, we believe that this simple, yet powerful method can become a standard tool for many problems. Extensive experimental results for a range of practical settings are reported.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge