Learning from Synthetic Data: Limitations of ERM

The prevalence and low cost of LLMs have led to a rise of synthetic content. From review sites to court documents, ``natural'' content has been contaminated by data points that appear similar to natural data, but are in fact LLM-generated. In this work we revisit fundamental learning theory questions in this, now ubiquitous, setting. We model this scenario as a sequence of learning tasks where the input is a mix of natural and synthetic data, and the learning algorithms are oblivious to the origin of any individual example. We study the possibilities and limitations of ERM in this setting. For the problem of estimating the mean of an arbitrary $d$-dimensional distribution, we find that while ERM converges to the true mean, it is outperformed by an algorithm that assigns non-uniform weights to examples from different generations of data. For the PAC learning setting, the disparity is even more stark. We find that ERM does not always converge to the true concept, echoing the model collapse literature. However, we show there are algorithms capable of learning the correct hypothesis for arbitrary VC classes and arbitrary amounts of contamination.

Clustering and Median Aggregation Improve Differentially Private Inference

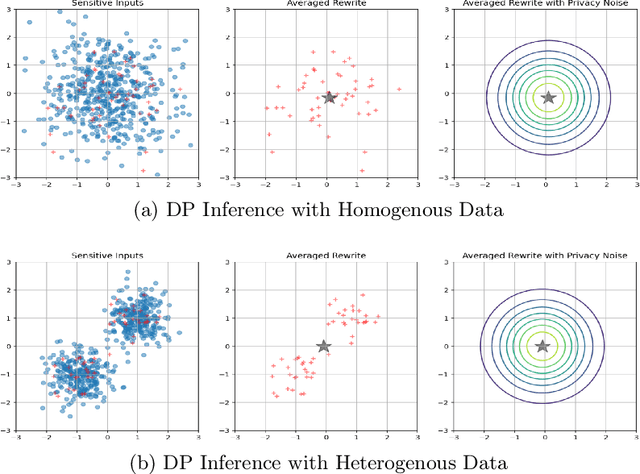
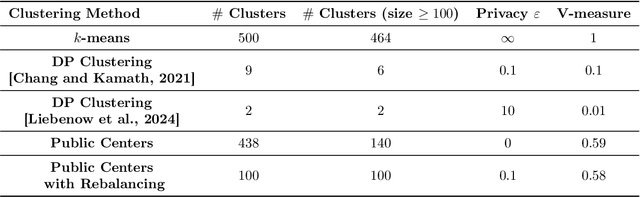
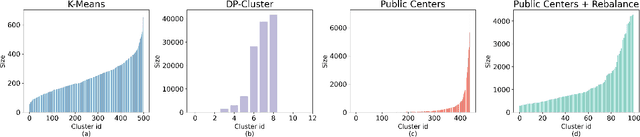
Differentially private (DP) language model inference is an approach for generating private synthetic text. A sensitive input example is used to prompt an off-the-shelf large language model (LLM) to produce a similar example. Multiple examples can be aggregated together to formally satisfy the DP guarantee. Prior work creates inference batches by sampling sensitive inputs uniformly at random. We show that uniform sampling degrades the quality of privately generated text, especially when the sensitive examples concern heterogeneous topics. We remedy this problem by clustering the input data before selecting inference batches. Next, we observe that clustering also leads to more similar next-token predictions across inferences. We use this insight to introduce a new algorithm that aggregates next token statistics by privately computing medians instead of averages. This approach leverages the fact that the median has decreased local sensitivity when next token predictions are similar, allowing us to state a data-dependent and ex-post DP guarantee about the privacy properties of this algorithm. Finally, we demonstrate improvements in terms of representativeness metrics (e.g., MAUVE) as well as downstream task performance. We show that our method produces high-quality synthetic data at significantly lower privacy cost than a previous state-of-the-art method.

Escaping Collapse: The Strength of Weak Data for Large Language Model Training

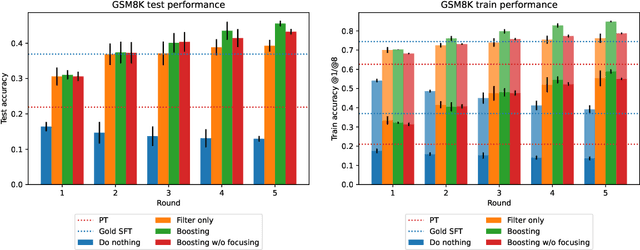
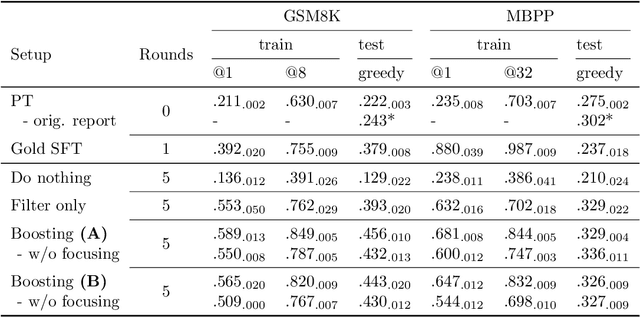
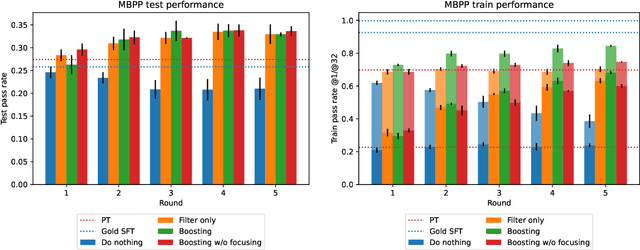
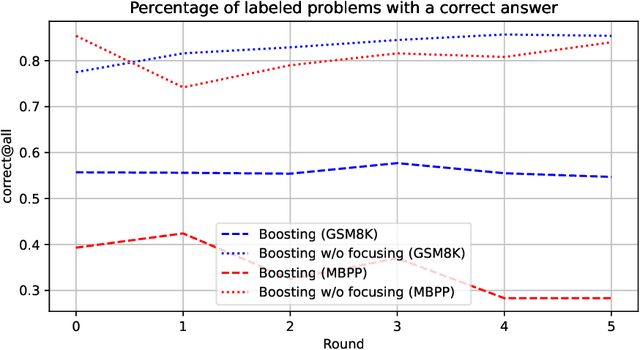
Synthetically-generated data plays an increasingly larger role in training large language models. However, while synthetic data has been found to be useful, studies have also shown that without proper curation it can cause LLM performance to plateau, or even "collapse", after many training iterations. In this paper, we formalize this question and develop a theoretical framework to investigate how much curation is needed in order to ensure that LLM performance continually improves. We find that the requirements are nearly minimal. We describe a training procedure that converges to an optimal LLM even if almost all of the non-synthetic training data is of poor quality. Our analysis is inspired by boosting, a classic machine learning technique that leverages a very weak learning algorithm to produce an arbitrarily good classifier. Our training procedure subsumes many recently proposed methods for training LLMs on synthetic data, and thus our analysis sheds light on why they are successful, and also suggests opportunities for future improvement. We present experiments that validate our theory, and show that dynamically focusing labeling resources on the most challenging examples -- in much the same way that boosting focuses the efforts of the weak learner -- leads to improved performance.

Private prediction for large-scale synthetic text generation

We present an approach for generating differentially private synthetic text using large language models (LLMs), via private prediction. In the private prediction framework, we only require the output synthetic data to satisfy differential privacy guarantees. This is in contrast to approaches that train a generative model on potentially sensitive user-supplied source data and seek to ensure the model itself is safe to release. We prompt a pretrained LLM with source data, but ensure that next-token predictions are made with differential privacy guarantees. Previous work in this paradigm reported generating a small number of examples (<10) at reasonable privacy levels, an amount of data that is useful only for downstream in-context learning or prompting. In contrast, we make changes that allow us to generate thousands of high-quality synthetic data points, greatly expanding the set of potential applications. Our improvements come from an improved privacy analysis and a better private selection mechanism, which makes use of the equivalence between the softmax layer for sampling tokens in LLMs and the exponential mechanism. Furthermore, we introduce a novel use of public predictions via the sparse vector technique, in which we do not pay privacy costs for tokens that are predictable without sensitive data; we find this to be particularly effective for structured data.

Private Algorithms with Private Predictions

When applying differential privacy to sensitive data, a common way of getting improved performance is to use external information such as other sensitive data, public data, or human priors. We propose to use the algorithms with predictions framework -- previously applied largely to improve time complexity or competitive ratios -- as a powerful way of designing and analyzing privacy-preserving methods that can take advantage of such external information to improve utility. For four important tasks -- quantile release, its extension to multiple quantiles, covariance estimation, and data release -- we construct prediction-dependent differentially private methods whose utility scales with natural measures of prediction quality. The analyses enjoy several advantages, including minimal assumptions about the data, natural ways of adding robustness to noisy predictions, and novel "meta" algorithms that can learn predictions from other (potentially sensitive) data. Overall, our results demonstrate how to enable differentially private algorithms to make use of and learn noisy predictions, which holds great promise for improving utility while preserving privacy across a variety of tasks.

Easy Differentially Private Linear Regression

Linear regression is a fundamental tool for statistical analysis. This has motivated the development of linear regression methods that also satisfy differential privacy and thus guarantee that the learned model reveals little about any one data point used to construct it. However, existing differentially private solutions assume that the end user can easily specify good data bounds and hyperparameters. Both present significant practical obstacles. In this paper, we study an algorithm which uses the exponential mechanism to select a model with high Tukey depth from a collection of non-private regression models. Given $n$ samples of $d$-dimensional data used to train $m$ models, we construct an efficient analogue using an approximate Tukey depth that runs in time $O(d^2n + dm\log(m))$. We find that this algorithm obtains strong empirical performance in the data-rich setting with no data bounds or hyperparameter selection required.

Learning with User-Level Privacy

We propose and analyze algorithms to solve a range of learning tasks under user-level differential privacy constraints. Rather than guaranteeing only the privacy of individual samples, user-level DP protects a user's entire contribution ($m \ge 1$ samples), providing more stringent but more realistic protection against information leaks. We show that for high-dimensional mean estimation, empirical risk minimization with smooth losses, stochastic convex optimization, and learning hypothesis class with finite metric entropy, the privacy cost decreases as $O(1/\sqrt{m})$ as users provide more samples. In contrast, when increasing the number of users $n$, the privacy cost decreases at a faster $O(1/n)$ rate. We complement these results with lower bounds showing the worst-case optimality of our algorithm for mean estimation and stochastic convex optimization. Our algorithms rely on novel techniques for private mean estimation in arbitrary dimension with error scaling as the concentration radius $\tau$ of the distribution rather than the entire range. Under uniform convergence, we derive an algorithm that privately answers a sequence of $K$ adaptively chosen queries with privacy cost proportional to $\tau$, and apply it to solve the learning tasks we consider.

Pan-Private Uniformity Testing

A centrally differentially private algorithm maps raw data to differentially private outputs. In contrast, a locally differentially private algorithm may only access data through public interaction with data holders, and this interaction must be a differentially private function of the data. We study the intermediate model of pan-privacy. Unlike a locally private algorithm, a pan-private algorithm receives data in the clear. Unlike a centrally private algorithm, the algorithm receives data one element at a time and must maintain a differentially private internal state while processing this stream. First, we show that pan-privacy against multiple intrusions on the internal state is equivalent to sequentially interactive local privacy. Next, we contextualize pan-privacy against a single intrusion by analyzing the sample complexity of uniformity testing over domain $[k]$. Focusing on the dependence on $k$, centrally private uniformity testing has sample complexity $\Theta(\sqrt{k})$, while noninteractive locally private uniformity testing has sample complexity $\Theta(k)$. We show that the sample complexity of pan-private uniformity testing is $\Theta(k^{2/3})$. By a new $\Omega(k)$ lower bound for the sequentially interactive setting, we also separate pan-private from sequentially interactive locally private and multi-intrusion pan-private uniformity testing.

Repeated Inverse Reinforcement Learning

We introduce a novel repeated Inverse Reinforcement Learning problem: the agent has to act on behalf of a human in a sequence of tasks and wishes to minimize the number of tasks that it surprises the human by acting suboptimally with respect to how the human would have acted. Each time the human is surprised, the agent is provided a demonstration of the desired behavior by the human. We formalize this problem, including how the sequence of tasks is chosen, in a few different ways and provide some foundational results.

Towards Resolving Unidentifiability in Inverse Reinforcement Learning

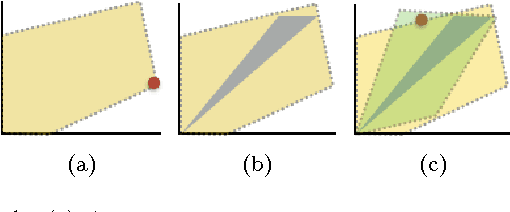
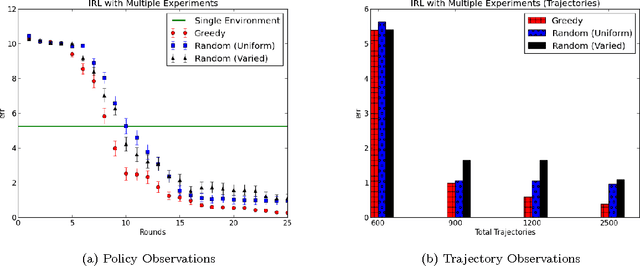
We consider a setting for Inverse Reinforcement Learning (IRL) where the learner is extended with the ability to actively select multiple environments, observing an agent's behavior on each environment. We first demonstrate that if the learner can experiment with any transition dynamics on some fixed set of states and actions, then there exists an algorithm that reconstructs the agent's reward function to the fullest extent theoretically possible, and that requires only a small (logarithmic) number of experiments. We contrast this result to what is known about IRL in single fixed environments, namely that the true reward function is fundamentally unidentifiable. We then extend this setting to the more realistic case where the learner may not select any transition dynamic, but rather is restricted to some fixed set of environments that it may try. We connect the problem of maximizing the information derived from experiments to submodular function maximization and demonstrate that a greedy algorithm is near optimal (up to logarithmic factors). Finally, we empirically validate our algorithm on an environment inspired by behavioral psychology.