Towards Resolving Unidentifiability in Inverse Reinforcement Learning
Paper and Code
Jan 25, 2016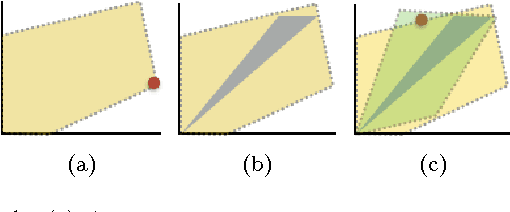

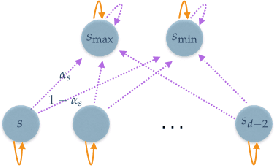
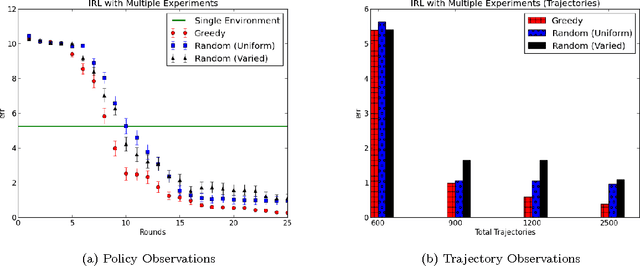
We consider a setting for Inverse Reinforcement Learning (IRL) where the learner is extended with the ability to actively select multiple environments, observing an agent's behavior on each environment. We first demonstrate that if the learner can experiment with any transition dynamics on some fixed set of states and actions, then there exists an algorithm that reconstructs the agent's reward function to the fullest extent theoretically possible, and that requires only a small (logarithmic) number of experiments. We contrast this result to what is known about IRL in single fixed environments, namely that the true reward function is fundamentally unidentifiable. We then extend this setting to the more realistic case where the learner may not select any transition dynamic, but rather is restricted to some fixed set of environments that it may try. We connect the problem of maximizing the information derived from experiments to submodular function maximization and demonstrate that a greedy algorithm is near optimal (up to logarithmic factors). Finally, we empirically validate our algorithm on an environment inspired by behavioral psychology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge