Mónica Ribero
Sequentially Auditing Differential Privacy
Sep 08, 2025
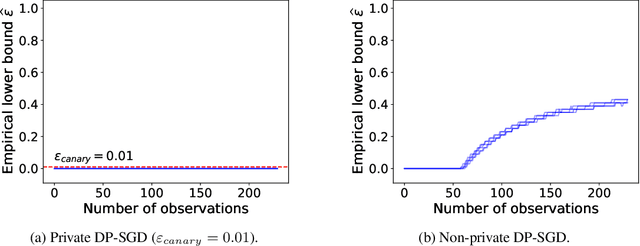
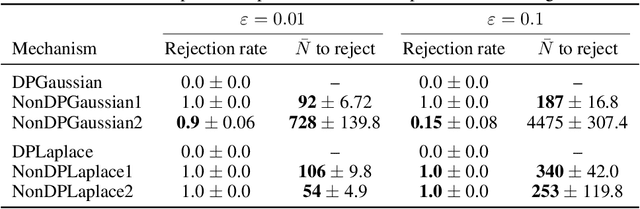
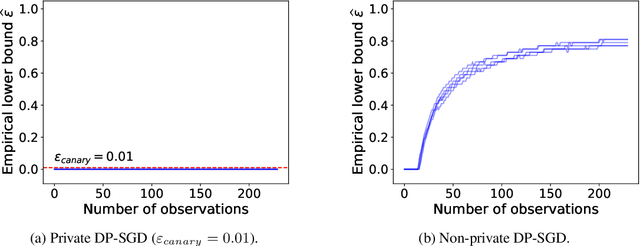
Abstract:We propose a practical sequential test for auditing differential privacy guarantees of black-box mechanisms. The test processes streams of mechanisms' outputs providing anytime-valid inference while controlling Type I error, overcoming the fixed sample size limitation of previous batch auditing methods. Experiments show this test detects violations with sample sizes that are orders of magnitude smaller than existing methods, reducing this number from 50K to a few hundred examples, across diverse realistic mechanisms. Notably, it identifies DP-SGD privacy violations in \textit{under} one training run, unlike prior methods needing full model training.
Privacy of the last iterate in cyclically-sampled DP-SGD on nonconvex composite losses
Jul 07, 2024
Abstract:Differentially private stochastic gradient descent (DP-SGD) refers to a family of optimization algorithms that provide a guaranteed level of differential privacy (DP) through DP accounting techniques. However, current accounting techniques make assumptions that diverge significantly from practical DP-SGD implementations. For example, they may assume the loss function is Lipschitz continuous and convex, sample the batches randomly with replacement, or omit the gradient clipping step. In this work, we analyze the most commonly used variant of DP-SGD, in which we sample batches cyclically with replacement, perform gradient clipping, and only release the last DP-SGD iterate. More specifically - without assuming convexity, smoothness, or Lipschitz continuity of the loss function - we establish new R\'enyi differential privacy (RDP) bounds for the last DP-SGD iterate under the mild assumption that (i) the DP-SGD stepsize is small relative to the topological constants in the loss function, and (ii) the loss function is weakly-convex. Moreover, we show that our bounds converge to previously established convex bounds when the weak-convexity parameter of the objective function approaches zero. In the case of non-Lipschitz smooth loss functions, we provide a weaker bound that scales well in terms of the number of DP-SGD iterations.
DP-SGD for non-decomposable objective functions
Oct 04, 2023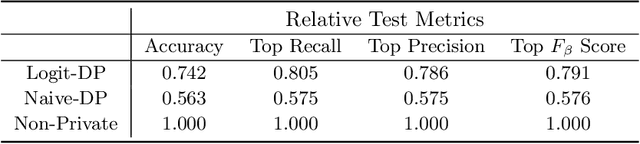
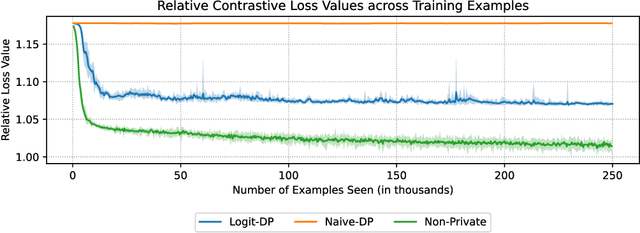
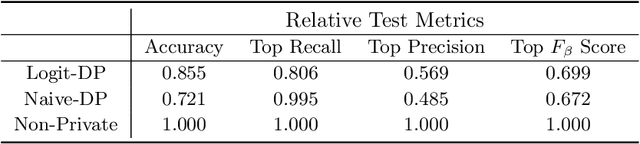
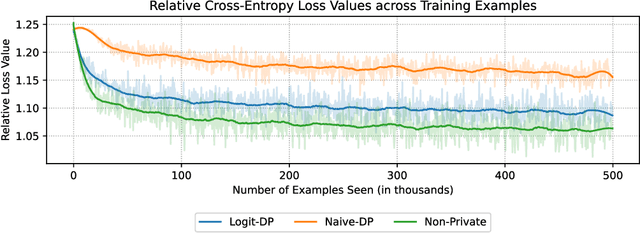
Abstract:Unsupervised pre-training is a common step in developing computer vision models and large language models. In this setting, the absence of labels requires the use of similarity-based loss functions, such as contrastive loss, that favor minimizing the distance between similar inputs and maximizing the distance between distinct inputs. As privacy concerns mount, training these models using differential privacy has become more important. However, due to how inputs are generated for these losses, one of their undesirable properties is that their $L_2$ sensitivity can grow with increasing batch size. This property is particularly disadvantageous for differentially private training methods, such as DP-SGD. To overcome this issue, we develop a new DP-SGD variant for similarity based loss functions -- in particular the commonly used contrastive loss -- that manipulates gradients of the objective function in a novel way to obtain a senstivity of the summed gradient that is $O(1)$ for batch size $n$. We test our DP-SGD variant on some preliminary CIFAR-10 pre-training and CIFAR-100 finetuning tasks and show that, in both tasks, our method's performance comes close to that of a non-private model and generally outperforms DP-SGD applied directly to the contrastive loss.
Easy Differentially Private Linear Regression
Aug 15, 2022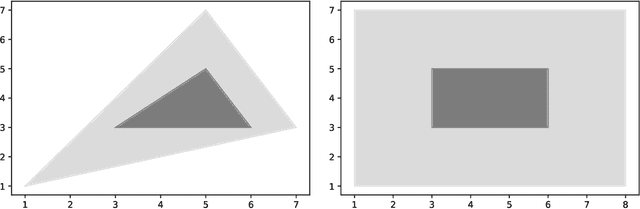



Abstract:Linear regression is a fundamental tool for statistical analysis. This has motivated the development of linear regression methods that also satisfy differential privacy and thus guarantee that the learned model reveals little about any one data point used to construct it. However, existing differentially private solutions assume that the end user can easily specify good data bounds and hyperparameters. Both present significant practical obstacles. In this paper, we study an algorithm which uses the exponential mechanism to select a model with high Tukey depth from a collection of non-private regression models. Given $n$ samples of $d$-dimensional data used to train $m$ models, we construct an efficient analogue using an approximate Tukey depth that runs in time $O(d^2n + dm\log(m))$. We find that this algorithm obtains strong empirical performance in the data-rich setting with no data bounds or hyperparameter selection required.
Dimension Independence in Unconstrained Private ERM via Adaptive Preconditioning
Aug 14, 2020
Abstract:In this paper we revisit the problem of private empirical risk minimziation (ERM) with differential privacy. We show that for unconstrained convex empirical risk minimization if the observed gradients of the objective function along the path of private gradient descent lie in a low-dimensional subspace (smaller than the ambient dimensionality of $p$), then using noisy adaptive preconditioning (a.k.a., noisy Adaptive Gradient Descent (AdaGrad)) we obtain a regret composed of two terms: a constant multiplicative factor of the original AdaGrad regret and an additional regret due to noise. In particular, we show that if the gradients lie in a constant rank subspace, then one can achieve an excess empirical risk of $ \tilde{O}(1/\epsilon n)$, compared to the worst-case achievable bound of $\tilde{O}(\sqrt{p}/\epsilon n)$. While previous works show dimension independent excess empirical risk bounds for the restrictive setting of convex generalized linear problems optimized over unconstrained subspaces, our results operate with general convex functions in unconstrained minimization. Along the way, we do a perturbation analysis of noisy AdaGrad, which may be of independent interest.
Federating Recommendations Using Differentially Private Prototypes
Mar 01, 2020



Abstract:Machine learning methods allow us to make recommendations to users in applications across fields including entertainment, dating, and commerce, by exploiting similarities in users' interaction patterns. However, in domains that demand protection of personally sensitive data, such as medicine or banking, how can we learn such a model without accessing the sensitive data, and without inadvertently leaking private information? We propose a new federated approach to learning global and local private models for recommendation without collecting raw data, user statistics, or information about personal preferences. Our method produces a set of prototypes that allows us to infer global behavioral patterns, while providing differential privacy guarantees for users in any database of the system. By requiring only two rounds of communication, we both reduce the communication costs and avoid the excessive privacy loss associated with iterative procedures. We test our framework on synthetic data as well as real federated medical data and Movielens ratings data. We show local adaptation of the global model allows our method to outperform centralized matrix-factorization-based recommender system models, both in terms of accuracy of matrix reconstruction and in terms of relevance of the recommendations, while maintaining provable privacy guarantees. We also show that our method is more robust and is characterized by smaller variance than individual models learned by independent entities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge