Outlier-Robust Optimal Transport: Duality, Structure, and Statistical Analysis
Paper and Code
Nov 05, 2021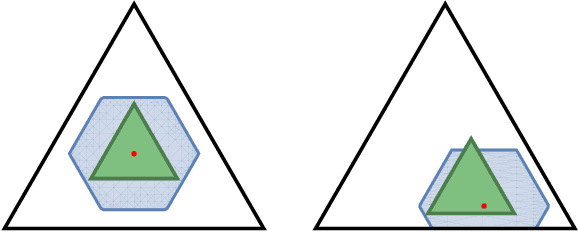
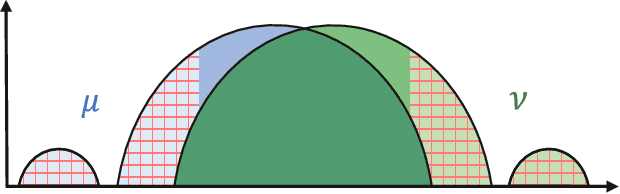
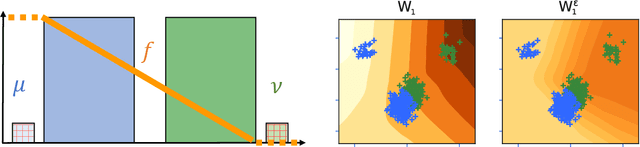

The Wasserstein distance, rooted in optimal transport (OT) theory, is a popular discrepancy measure between probability distributions with various applications to statistics and machine learning. Despite their rich structure and demonstrated utility, Wasserstein distances are sensitive to outliers in the considered distributions, which hinders applicability in practice. Inspired by the Huber contamination model, we propose a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from each contaminated distribution. Our formulation amounts to a highly regular optimization problem that lends itself better for analysis compared to previously considered frameworks. Leveraging this, we conduct a thorough theoretical study of $\mathsf{W}_p^\varepsilon$, encompassing characterization of optimal perturbations, regularity, duality, and statistical estimation and robustness results. In particular, by decoupling the optimization variables, we arrive at a simple dual form for $\mathsf{W}_p^\varepsilon$ that can be implemented via an elementary modification to standard, duality-based OT solvers. We illustrate the benefits of our framework via applications to generative modeling with contaminated datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge