Sloan Nietert
Estimation of Stochastic Optimal Transport Maps
Dec 10, 2025Abstract:The optimal transport (OT) map is a geometry-driven transformation between high-dimensional probability distributions which underpins a wide range of tasks in statistics, applied probability, and machine learning. However, existing statistical theory for OT map estimation is quite restricted, hinging on Brenier's theorem (quadratic cost, absolutely continuous source) to guarantee existence and uniqueness of a deterministic OT map, on which various additional regularity assumptions are imposed to obtain quantitative error bounds. In many real-world problems these conditions fail or cannot be certified, in which case optimal transportation is possible only via stochastic maps that can split mass. To broaden the scope of map estimation theory to such settings, this work introduces a novel metric for evaluating the transportation quality of stochastic maps. Under this metric, we develop computationally efficient map estimators with near-optimal finite-sample risk bounds, subject to easy-to-verify minimal assumptions. Our analysis further accommodates common forms of adversarial sample contamination, yielding estimators with robust estimation guarantees. Empirical experiments are provided which validate our theory and demonstrate the utility of the proposed framework in settings where existing theory fails. These contributions constitute the first general-purpose theory for map estimation, compatible with a wide spectrum of real-world applications where optimal transport may be intrinsically stochastic.
Contextual Dynamic Pricing with Heterogeneous Buyers
Dec 10, 2025Abstract:We initiate the study of contextual dynamic pricing with a heterogeneous population of buyers, where a seller repeatedly posts prices (over $T$ rounds) that depend on the observable $d$-dimensional context and receives binary purchase feedback. Unlike prior work assuming homogeneous buyer types, in our setting the buyer's valuation type is drawn from an unknown distribution with finite support size $K_{\star}$. We develop a contextual pricing algorithm based on optimistic posterior sampling with regret $\widetilde{O}(K_{\star}\sqrt{dT})$, which we prove to be tight in $d$ and $T$ up to logarithmic terms. Finally, we refine our analysis for the non-contextual pricing case, proposing a variance-aware zooming algorithm that achieves the optimal dependence on $K_{\star}$.
Robust Alignment via Partial Gromov-Wasserstein Distances
Jun 26, 2025Abstract:The Gromov-Wasserstein (GW) problem provides a powerful framework for aligning heterogeneous datasets by matching their internal structures in a way that minimizes distortion. However, GW alignment is sensitive to data contamination by outliers, which can greatly distort the resulting matching scheme. To address this issue, we study robust GW alignment, where upon observing contaminated versions of the clean data distributions, our goal is to accurately estimate the GW alignment cost between the original (uncontaminated) measures. We propose an estimator based on the partial GW distance, which trims out a fraction of the mass from each distribution before optimally aligning the rest. The estimator is shown to be minimax optimal in the population setting and is near-optimal in the finite-sample regime, where the optimality gap originates only from the suboptimality of the plug-in estimator in the empirical estimation setting (i.e., without contamination). Towards the analysis, we derive new structural results pertaining to the approximate pseudo-metric structure of the partial GW distance. Overall, our results endow the partial GW distance with an operational meaning by posing it as a robust surrogate of the classical distance when the observed data may be contaminated.
Robust Distribution Learning with Local and Global Adversarial Corruptions
Jun 10, 2024Abstract:We consider learning in an adversarial environment, where an $\varepsilon$-fraction of samples from a distribution $P$ are arbitrarily modified (*global* corruptions) and the remaining perturbations have average magnitude bounded by $\rho$ (*local* corruptions). Given access to $n$ such corrupted samples, we seek a computationally efficient estimator $\hat{P}_n$ that minimizes the Wasserstein distance $\mathsf{W}_1(\hat{P}_n,P)$. In fact, we attack the fine-grained task of minimizing $\mathsf{W}_1(\Pi_\# \hat{P}_n, \Pi_\# P)$ for all orthogonal projections $\Pi \in \mathbb{R}^{d \times d}$, with performance scaling with $\mathrm{rank}(\Pi) = k$. This allows us to account simultaneously for mean estimation ($k=1$), distribution estimation ($k=d$), as well as the settings interpolating between these two extremes. We characterize the optimal population-limit risk for this task and then develop an efficient finite-sample algorithm with error bounded by $\sqrt{\varepsilon k} + \rho + d^{O(1)}\tilde{O}(n^{-1/k})$ when $P$ has bounded moments of order $2+\delta$, for constant $\delta > 0$. For data distributions with bounded covariance, our finite-sample bounds match the minimax population-level optimum for large sample sizes. Our efficient procedure relies on a novel trace norm approximation of an ideal yet intractable 2-Wasserstein projection estimator. We apply this algorithm to robust stochastic optimization, and, in the process, uncover a new method for overcoming the curse of dimensionality in Wasserstein distributionally robust optimization.
Outlier-Robust Wasserstein DRO
Nov 09, 2023Abstract:Distributionally robust optimization (DRO) is an effective approach for data-driven decision-making in the presence of uncertainty. Geometric uncertainty due to sampling or localized perturbations of data points is captured by Wasserstein DRO (WDRO), which seeks to learn a model that performs uniformly well over a Wasserstein ball centered around the observed data distribution. However, WDRO fails to account for non-geometric perturbations such as adversarial outliers, which can greatly distort the Wasserstein distance measurement and impede the learned model. We address this gap by proposing a novel outlier-robust WDRO framework for decision-making under both geometric (Wasserstein) perturbations and non-geometric (total variation (TV)) contamination that allows an $\varepsilon$-fraction of data to be arbitrarily corrupted. We design an uncertainty set using a certain robust Wasserstein ball that accounts for both perturbation types and derive minimax optimal excess risk bounds for this procedure that explicitly capture the Wasserstein and TV risks. We prove a strong duality result that enables tractable convex reformulations and efficient computation of our outlier-robust WDRO problem. When the loss function depends only on low-dimensional features of the data, we eliminate certain dimension dependencies from the risk bounds that are unavoidable in the general setting. Finally, we present experiments validating our theory on standard regression and classification tasks.
Robust Estimation under the Wasserstein Distance
Feb 02, 2023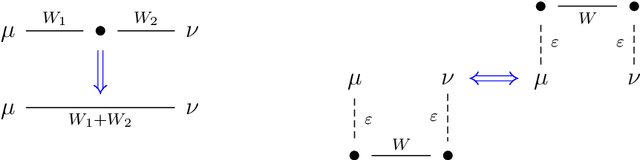

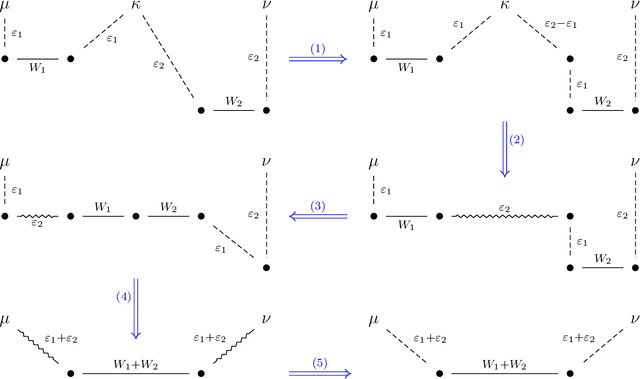
Abstract:We study the problem of robust distribution estimation under the Wasserstein metric, a popular discrepancy measure between probability distributions rooted in optimal transport (OT) theory. We introduce a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from its input distributions, and show that minimum distance estimation under $\mathsf{W}_p^\varepsilon$ achieves minimax optimal robust estimation risk. Our analysis is rooted in several new results for partial OT, including an approximate triangle inequality, which may be of independent interest. To address computational tractability, we derive a dual formulation for $\mathsf{W}_p^\varepsilon$ that adds a simple penalty term to the classic Kantorovich dual objective. As such, $\mathsf{W}_p^\varepsilon$ can be implemented via an elementary modification to standard, duality-based OT solvers. Our results are extended to sliced OT, where distributions are projected onto low-dimensional subspaces, and applications to homogeneity and independence testing are explored. We illustrate the virtues of our framework via applications to generative modeling with contaminated datasets.
Statistical, Robustness, and Computational Guarantees for Sliced Wasserstein Distances
Oct 17, 2022



Abstract:Sliced Wasserstein distances preserve properties of classic Wasserstein distances while being more scalable for computation and estimation in high dimensions. The goal of this work is to quantify this scalability from three key aspects: (i) empirical convergence rates; (ii) robustness to data contamination; and (iii) efficient computational methods. For empirical convergence, we derive fast rates with explicit dependence of constants on dimension, subject to log-concavity of the population distributions. For robustness, we characterize minimax optimal, dimension-free robust estimation risks, and show an equivalence between robust sliced 1-Wasserstein estimation and robust mean estimation. This enables lifting statistical and algorithmic guarantees available for the latter to the sliced 1-Wasserstein setting. Moving on to computational aspects, we analyze the Monte Carlo estimator for the average-sliced distance, demonstrating that larger dimension can result in faster convergence of the numerical integration error. For the max-sliced distance, we focus on a subgradient-based local optimization algorithm that is frequently used in practice, albeit without formal guarantees, and establish an $O(\epsilon^{-4})$ computational complexity bound for it. Our theory is validated by numerical experiments, which altogether provide a comprehensive quantitative account of the scalability question.
Learning in Stackelberg Games with Non-myopic Agents
Aug 19, 2022Abstract:We study Stackelberg games where a principal repeatedly interacts with a long-lived, non-myopic agent, without knowing the agent's payoff function. Although learning in Stackelberg games is well-understood when the agent is myopic, non-myopic agents pose additional complications. In particular, non-myopic agents may strategically select actions that are inferior in the present to mislead the principal's learning algorithm and obtain better outcomes in the future. We provide a general framework that reduces learning in presence of non-myopic agents to robust bandit optimization in the presence of myopic agents. Through the design and analysis of minimally reactive bandit algorithms, our reduction trades off the statistical efficiency of the principal's learning algorithm against its effectiveness in inducing near-best-responses. We apply this framework to Stackelberg security games (SSGs), pricing with unknown demand curve, strategic classification, and general finite Stackelberg games. In each setting, we characterize the type and impact of misspecifications present in near-best-responses and develop a learning algorithm robust to such misspecifications. Along the way, we improve the query complexity of learning in SSGs with $n$ targets from the state-of-the-art $O(n^3)$ to a near-optimal $\widetilde{O}(n)$ by uncovering a fundamental structural property of such games. This result is of independent interest beyond learning with non-myopic agents.
Outlier-Robust Optimal Transport: Duality, Structure, and Statistical Analysis
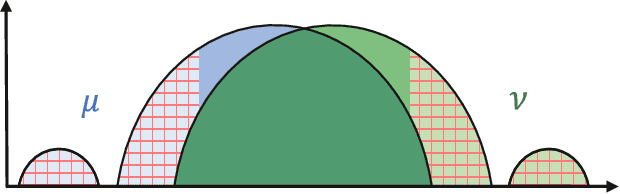
Nov 05, 2021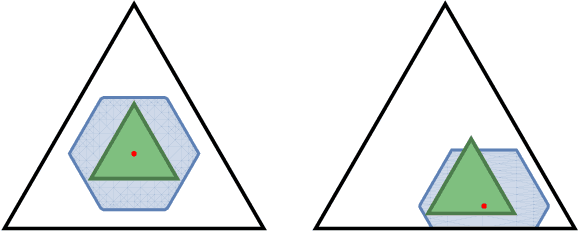
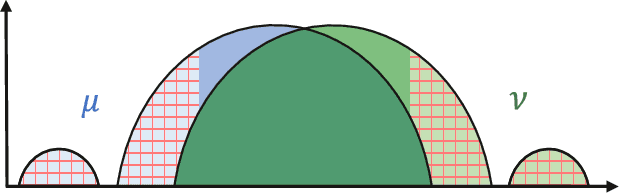
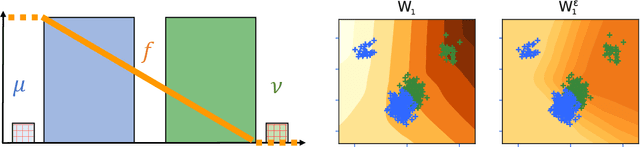

Abstract:The Wasserstein distance, rooted in optimal transport (OT) theory, is a popular discrepancy measure between probability distributions with various applications to statistics and machine learning. Despite their rich structure and demonstrated utility, Wasserstein distances are sensitive to outliers in the considered distributions, which hinders applicability in practice. Inspired by the Huber contamination model, we propose a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from each contaminated distribution. Our formulation amounts to a highly regular optimization problem that lends itself better for analysis compared to previously considered frameworks. Leveraging this, we conduct a thorough theoretical study of $\mathsf{W}_p^\varepsilon$, encompassing characterization of optimal perturbations, regularity, duality, and statistical estimation and robustness results. In particular, by decoupling the optimization variables, we arrive at a simple dual form for $\mathsf{W}_p^\varepsilon$ that can be implemented via an elementary modification to standard, duality-based OT solvers. We illustrate the benefits of our framework via applications to generative modeling with contaminated datasets.
From Smooth Wasserstein Distance to Dual Sobolev Norm: Empirical Approximation and Statistical Applications
Jan 14, 2021



Abstract:Statistical distances, i.e., discrepancy measures between probability distributions, are ubiquitous in probability theory, statistics and machine learning. To combat the curse of dimensionality when estimating these distances from data, recent work has proposed smoothing out local irregularities in the measured distributions via convolution with a Gaussian kernel. Motivated by the scalability of the smooth framework to high dimensions, we conduct an in-depth study of the structural and statistical behavior of the Gaussian-smoothed $p$-Wasserstein distance $\mathsf{W}_p^{(\sigma)}$, for arbitrary $p\geq 1$. We start by showing that $\mathsf{W}_p^{(\sigma)}$ admits a metric structure that is topologically equivalent to classic $\mathsf{W}_p$ and is stable with respect to perturbations in $\sigma$. Moving to statistical questions, we explore the asymptotic properties of $\mathsf{W}_p^{(\sigma)}(\hat{\mu}_n,\mu)$, where $\hat{\mu}_n$ is the empirical distribution of $n$ i.i.d. samples from $\mu$. To that end, we prove that $\mathsf{W}_p^{(\sigma)}$ is controlled by a $p$th order smooth dual Sobolev norm $\mathsf{d}_p^{(\sigma)}$. Since $\mathsf{d}_p^{(\sigma)}(\hat{\mu}_n,\mu)$ coincides with the supremum of an empirical process indexed by Gaussian-smoothed Sobolev functions, it lends itself well to analysis via empirical process theory. We derive the limit distribution of $\sqrt{n}\mathsf{d}_p^{(\sigma)}(\hat{\mu}_n,\mu)$ in all dimensions $d$, when $\mu$ is sub-Gaussian. Through the aforementioned bound, this implies a parametric empirical convergence rate of $n^{-1/2}$ for $\mathsf{W}_p^{(\sigma)}$, contrasting the $n^{-1/d}$ rate for unsmoothed $\mathsf{W}_p$ when $d \geq 3$. As applications, we provide asymptotic guarantees for two-sample testing and minimum distance estimation. When $p=2$, we further show that $\mathsf{d}_2^{(\sigma)}$ can be expressed as a maximum mean discrepancy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge