Time-Aware Synthetic Control

The synthetic control (SC) framework is widely used for observational causal inference with time-series panel data. SC has been successful in diverse applications, but existing methods typically treat the ordering of pre-intervention time indices interchangeable. This invariance means they may not fully take advantage of temporal structure when strong trends are present. We propose Time-Aware Synthetic Control (TASC), which employs a state-space model with a constant trend while preserving a low-rank structure of the signal. TASC uses the Kalman filter and Rauch-Tung-Striebel smoother: it first fits a generative time-series model with expectation-maximization and then performs counterfactual inference. We evaluate TASC on both simulated and real-world datasets, including policy evaluation and sports prediction. Our results suggest that TASC offers advantages in settings with strong temporal trends and high levels of observation noise.

ClusterSC: Advancing Synthetic Control with Donor Selection

In causal inference with observational studies, synthetic control (SC) has emerged as a prominent tool. SC has traditionally been applied to aggregate-level datasets, but more recent work has extended its use to individual-level data. As they contain a greater number of observed units, this shift introduces the curse of dimensionality to SC. To address this, we propose Cluster Synthetic Control (ClusterSC), based on the idea that groups of individuals may exist where behavior aligns internally but diverges between groups. ClusterSC incorporates a clustering step to select only the relevant donors for the target. We provide theoretical guarantees on the improvements induced by ClusterSC, supported by empirical demonstrations on synthetic and real-world datasets. The results indicate that ClusterSC consistently outperforms classical SC approaches.

Differentially Private Synthetic Control

Synthetic control is a causal inference tool used to estimate the treatment effects of an intervention by creating synthetic counterfactual data. This approach combines measurements from other similar observations (i.e., donor pool ) to predict a counterfactual time series of interest (i.e., target unit) by analyzing the relationship between the target and the donor pool before the intervention. As synthetic control tools are increasingly applied to sensitive or proprietary data, formal privacy protections are often required. In this work, we provide the first algorithms for differentially private synthetic control with explicit error bounds. Our approach builds upon tools from non-private synthetic control and differentially private empirical risk minimization. We provide upper and lower bounds on the sensitivity of the synthetic control query and provide explicit error bounds on the accuracy of our private synthetic control algorithms. We show that our algorithms produce accurate predictions for the target unit, and that the cost of privacy is small. Finally, we empirically evaluate the performance of our algorithm, and show favorable performance in a variety of parameter regimes, as well as providing guidance to practitioners for hyperparameter tuning.

Improved Differentially Private Regression via Gradient Boosting

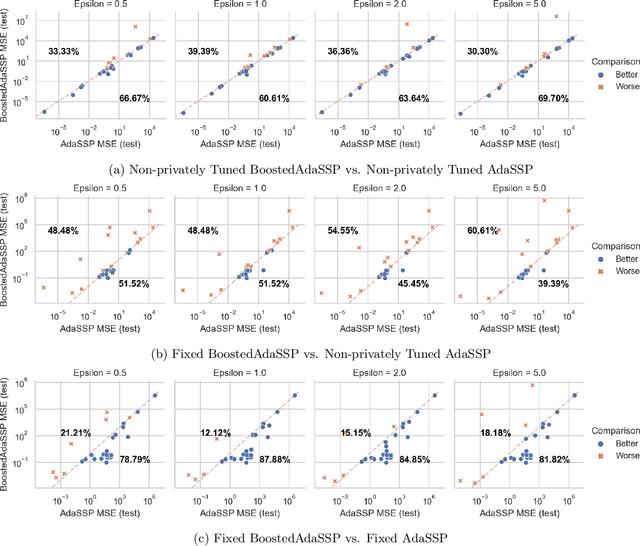
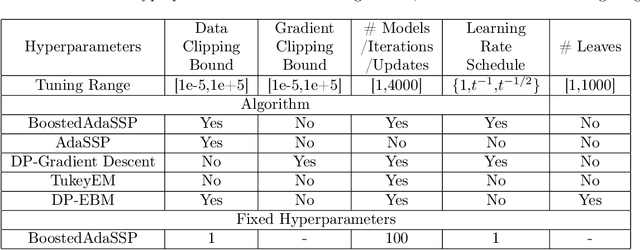
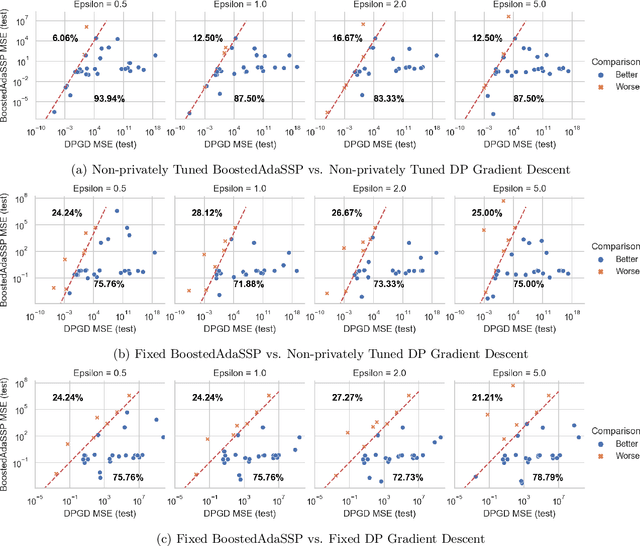
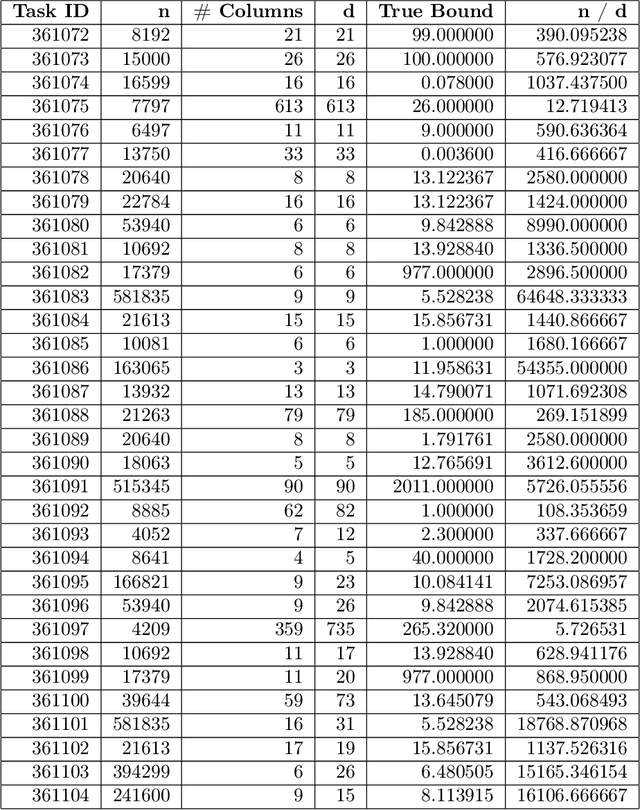
We revisit the problem of differentially private squared error linear regression. We observe that existing state-of-the-art methods are sensitive to the choice of hyper-parameters -- including the ``clipping threshold'' that cannot be set optimally in a data-independent way. We give a new algorithm for private linear regression based on gradient boosting. We show that our method consistently improves over the previous state of the art when the clipping threshold is taken to be fixed without knowledge of the data, rather than optimized in a non-private way -- and that even when we optimize the clipping threshold non-privately, our algorithm is no worse. In addition to a comprehensive set of experiments, we give theoretical insights to explain this behavior.