Improved Differentially Private Regression via Gradient Boosting
Paper and Code
Mar 06, 2023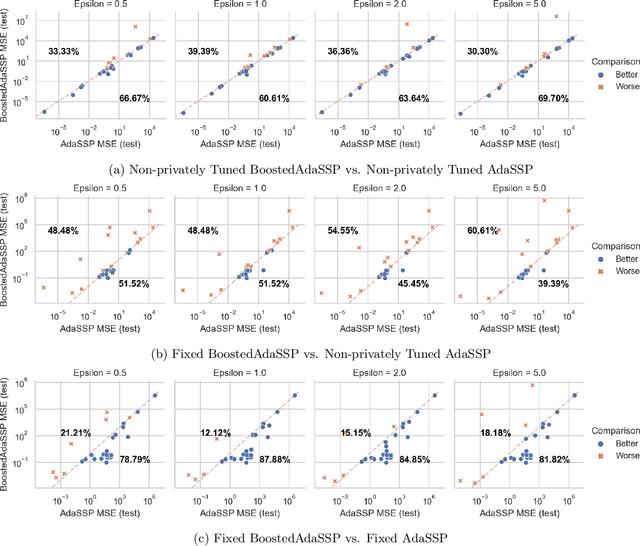
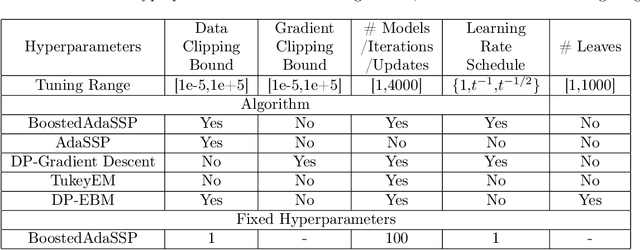
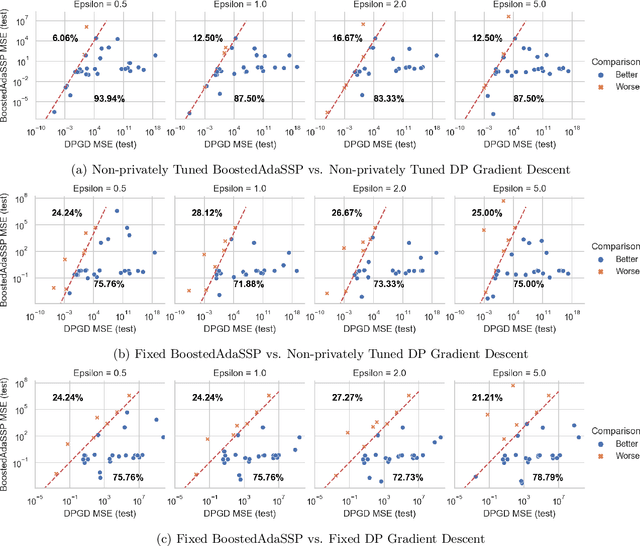
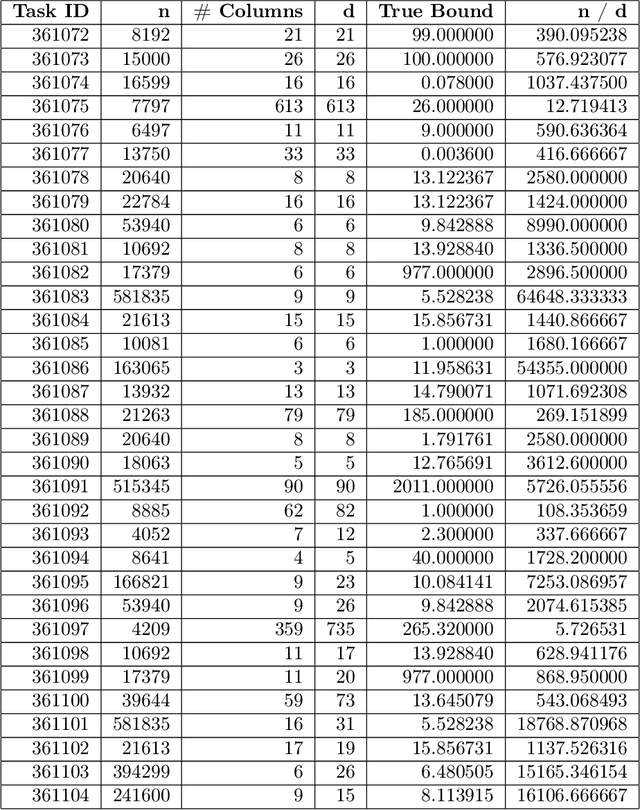
We revisit the problem of differentially private squared error linear regression. We observe that existing state-of-the-art methods are sensitive to the choice of hyper-parameters -- including the ``clipping threshold'' that cannot be set optimally in a data-independent way. We give a new algorithm for private linear regression based on gradient boosting. We show that our method consistently improves over the previous state of the art when the clipping threshold is taken to be fixed without knowledge of the data, rather than optimized in a non-private way -- and that even when we optimize the clipping threshold non-privately, our algorithm is no worse. In addition to a comprehensive set of experiments, we give theoretical insights to explain this behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge