Learning Dynamics of Deep Linear Networks Beyond the Edge of Stability

Deep neural networks trained using gradient descent with a fixed learning rate $\eta$ often operate in the regime of "edge of stability" (EOS), where the largest eigenvalue of the Hessian equilibrates about the stability threshold $2/\eta$. In this work, we present a fine-grained analysis of the learning dynamics of (deep) linear networks (DLNs) within the deep matrix factorization loss beyond EOS. For DLNs, loss oscillations beyond EOS follow a period-doubling route to chaos. We theoretically analyze the regime of the 2-period orbit and show that the loss oscillations occur within a small subspace, with the dimension of the subspace precisely characterized by the learning rate. The crux of our analysis lies in showing that the symmetry-induced conservation law for gradient flow, defined as the balancing gap among the singular values across layers, breaks at EOS and decays monotonically to zero. Overall, our results contribute to explaining two key phenomena in deep networks: (i) shallow models and simple tasks do not always exhibit EOS; and (ii) oscillations occur within top features. We present experiments to support our theory, along with examples demonstrating how these phenomena occur in nonlinear networks and how they differ from those which have benign landscape such as in DLNs.

Understanding Untrained Deep Models for Inverse Problems: Algorithms and Theory

In recent years, deep learning methods have been extensively developed for inverse imaging problems (IIPs), encompassing supervised, self-supervised, and generative approaches. Most of these methods require large amounts of labeled or unlabeled training data to learn effective models. However, in many practical applications, such as medical image reconstruction, extensive training datasets are often unavailable or limited. A significant milestone in addressing this challenge came in 2018 with the work of Ulyanov et al., which introduced the Deep Image Prior (DIP)--the first training-data-free neural network method for IIPs. Unlike conventional deep learning approaches, DIP requires only a convolutional neural network, the noisy measurements, and a forward operator. By leveraging the implicit regularization of deep networks initialized with random noise, DIP can learn and restore image structures without relying on external datasets. However, a well-known limitation of DIP is its susceptibility to overfitting, primarily due to the over-parameterization of the network. In this tutorial paper, we provide a comprehensive review of DIP, including a theoretical analysis of its training dynamics. We also categorize and discuss recent advancements in DIP-based methods aimed at mitigating overfitting, including techniques such as regularization, network re-parameterization, and early stopping. Furthermore, we discuss approaches that combine DIP with pre-trained neural networks, present empirical comparison results against data-centric methods, and highlight open research questions and future directions.

Pruning Unrolled Networks (PUN) at Initialization for MRI Reconstruction Improves Generalization

Deep learning methods are highly effective for many image reconstruction tasks. However, the performance of supervised learned models can degrade when applied to distinct experimental settings at test time or in the presence of distribution shifts. In this study, we demonstrate that pruning deep image reconstruction networks at training time can improve their robustness to distribution shifts. In particular, we consider unrolled reconstruction architectures for accelerated magnetic resonance imaging and introduce a method for pruning unrolled networks (PUN) at initialization. Our experiments demonstrate that when compared to traditional dense networks, PUN offers improved generalization across a variety of experimental settings and even slight performance gains on in-distribution data.

Optimal Eye Surgeon: Finding Image Priors through Sparse Generators at Initialization

We introduce Optimal Eye Surgeon (OES), a framework for pruning and training deep image generator networks. Typically, untrained deep convolutional networks, which include image sampling operations, serve as effective image priors (Ulyanov et al., 2018). However, they tend to overfit to noise in image restoration tasks due to being overparameterized. OES addresses this by adaptively pruning networks at random initialization to a level of underparameterization. This process effectively captures low-frequency image components even without training, by just masking. When trained to fit noisy images, these pruned subnetworks, which we term Sparse-DIP, resist overfitting to noise. This benefit arises from underparameterization and the regularization effect of masking, constraining them in the manifold of image priors. We demonstrate that subnetworks pruned through OES surpass other leading pruning methods, such as the Lottery Ticket Hypothesis, which is known to be suboptimal for image recovery tasks (Wu et al., 2023). Our extensive experiments demonstrate the transferability of OES-masks and the characteristics of sparse-subnetworks for image generation. Code is available at https://github.com/Avra98/Optimal-Eye-Surgeon.git.

Towards Understanding Task-agnostic Debiasing Through the Lenses of Intrinsic Bias and Forgetfulness

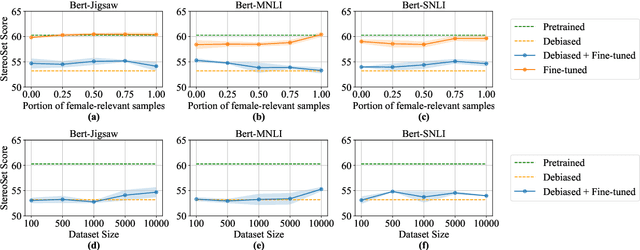
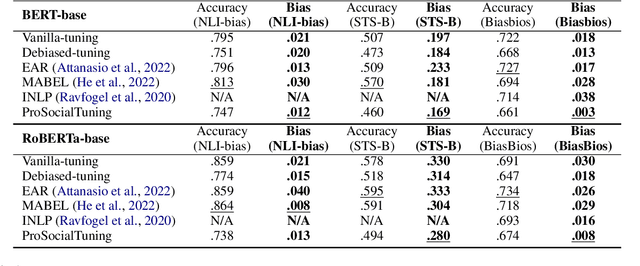
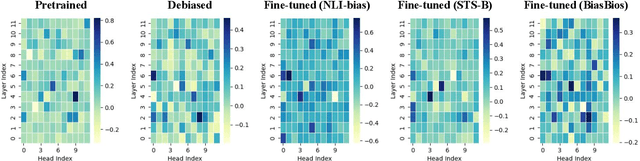
While task-agnostic debiasing provides notable generalizability and reduced reliance on downstream data, its impact on language modeling ability and the risk of relearning social biases from downstream task-specific data remain as the two most significant challenges when debiasing Pretrained Language Models (PLMs). The impact on language modeling ability can be alleviated given a high-quality and long-contextualized debiasing corpus, but there remains a deficiency in understanding the specifics of relearning biases. We empirically ascertain that the effectiveness of task-agnostic debiasing hinges on the quantitative bias level of both the task-specific data used for downstream applications and the debiased model. We empirically show that the lower bound of the bias level of the downstream fine-tuned model can be approximated by the bias level of the debiased model, in most practical cases. To gain more in-depth understanding about how the parameters of PLMs change during fine-tuning due to the forgetting issue of PLMs, we propose a novel framework which can Propagate Socially-fair Debiasing to Downstream Fine-tuning, ProSocialTuning. Our proposed framework can push the fine-tuned model to approach the bias lower bound during downstream fine-tuning, indicating that the ineffectiveness of debiasing can be alleviated by overcoming the forgetting issue through regularizing successfully debiased attention heads based on the PLMs' bias levels from stages of pretraining and debiasing.

Auto-tune: PAC-Bayes Optimization over Prior and Posterior for Neural Networks

It is widely recognized that the generalization ability of neural networks can be greatly enhanced through carefully designing the training procedure. The current state-of-the-art training approach involves utilizing stochastic gradient descent (SGD) or Adam optimization algorithms along with a combination of additional regularization techniques such as weight decay, dropout, or noise injection. Optimal generalization can only be achieved by tuning a multitude of hyperparameters through grid search, which can be time-consuming and necessitates additional validation datasets. To address this issue, we introduce a practical PAC-Bayes training framework that is nearly tuning-free and requires no additional regularization while achieving comparable testing performance to that of SGD/Adam after a complete grid search and with extra regularizations. Our proposed algorithm demonstrates the remarkable potential of PAC training to achieve state-of-the-art performance on deep neural networks with enhanced robustness and interpretability.

Implicit regularization in Heavy-ball momentum accelerated stochastic gradient descent

It is well known that the finite step-size ($h$) in Gradient Descent (GD) implicitly regularizes solutions to flatter minima. A natural question to ask is "Does the momentum parameter $\beta$ play a role in implicit regularization in Heavy-ball (H.B) momentum accelerated gradient descent (GD+M)?". To answer this question, first, we show that the discrete H.B momentum update (GD+M) follows a continuous trajectory induced by a modified loss, which consists of an original loss and an implicit regularizer. Then, we show that this implicit regularizer for (GD+M) is stronger than that of (GD) by factor of $(\frac{1+\beta}{1-\beta})$, thus explaining why (GD+M) shows better generalization performance and higher test accuracy than (GD). Furthermore, we extend our analysis to the stochastic version of gradient descent with momentum (SGD+M) and characterize the continuous trajectory of the update of (SGD+M) in a pointwise sense. We explore the implicit regularization in (SGD+M) and (GD+M) through a series of experiments validating our theory.

Learning Sparsity-Promoting Regularizers using Bilevel Optimization

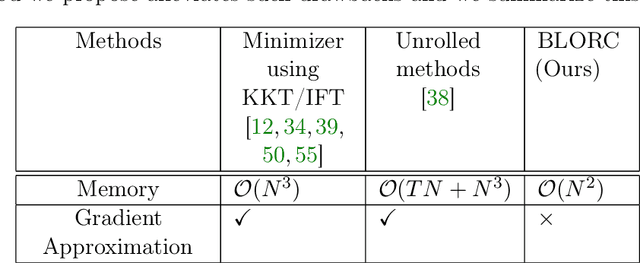
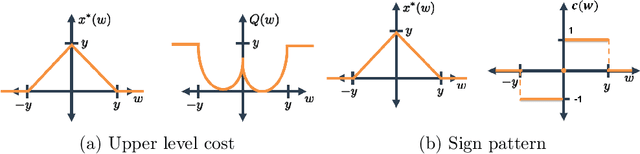
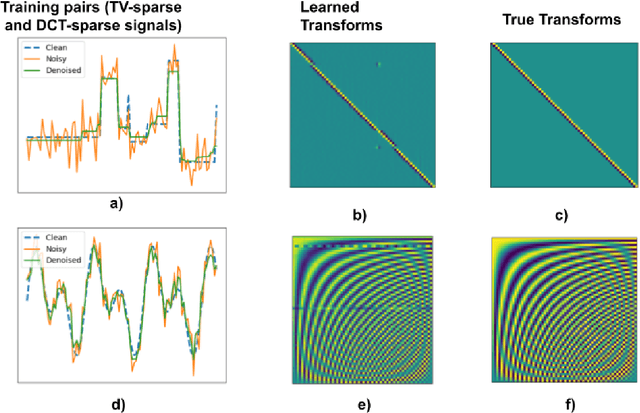
We present a method for supervised learning of sparsity-promoting regularizers for denoising signals and images. Sparsity-promoting regularization is a key ingredient in solving modern signal reconstruction problems; however, the operators underlying these regularizers are usually either designed by hand or learned from data in an unsupervised way. The recent success of supervised learning (mainly convolutional neural networks) in solving image reconstruction problems suggests that it could be a fruitful approach to designing regularizers. Towards this end, we propose to denoise signals using a variational formulation with a parametric, sparsity-promoting regularizer, where the parameters of the regularizer are learned to minimize the mean squared error of reconstructions on a training set of ground truth image and measurement pairs. Training involves solving a challenging bilievel optimization problem; we derive an expression for the gradient of the training loss using the closed-form solution of the denoising problem and provide an accompanying gradient descent algorithm to minimize it. Our experiments with structured 1D signals and natural images show that the proposed method can learn an operator that outperforms well-known regularizers (total variation, DCT-sparsity, and unsupervised dictionary learning) and collaborative filtering for denoising. While the approach we present is specific to denoising, we believe that it could be adapted to the larger class of inverse problems with linear measurement models, giving it applicability in a wide range of signal reconstruction settings.

Bilevel learning of l1-regularizers with closed-form gradients(BLORC)

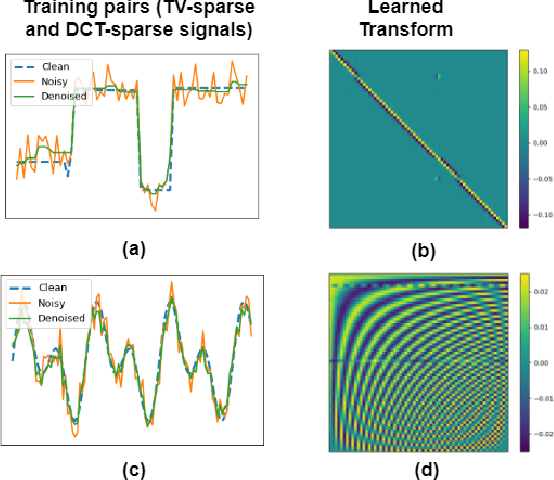
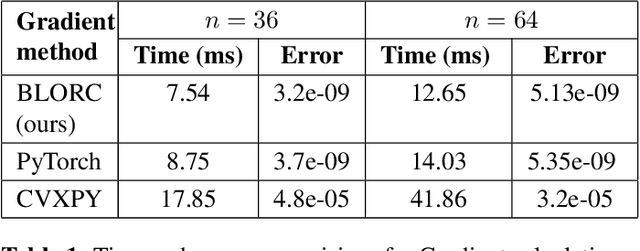
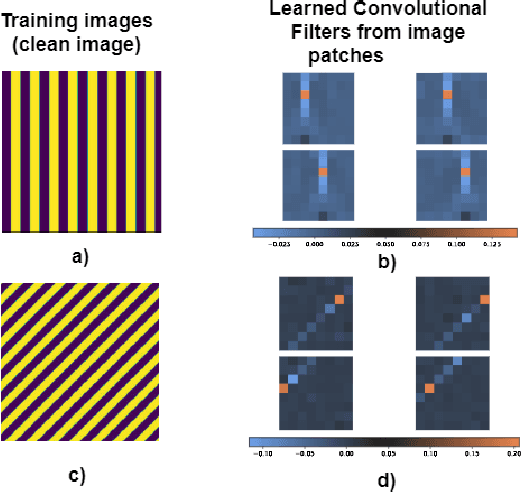
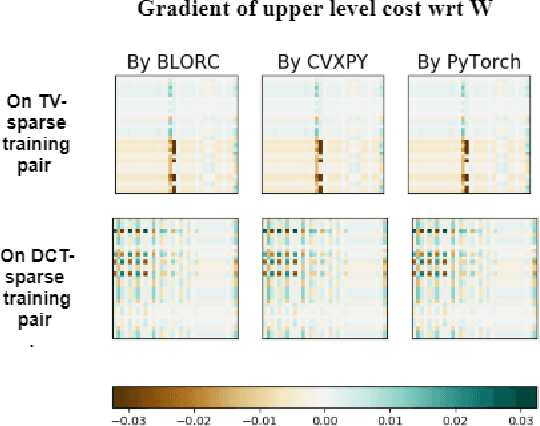
We present a method for supervised learning of sparsity-promoting regularizers, a key ingredient in many modern signal reconstruction problems. The parameters of the regularizer are learned to minimize the mean squared error of reconstruction on a training set of ground truth signal and measurement pairs. Training involves solving a challenging bilevel optimization problem with a nonsmooth lower-level objective. We derive an expression for the gradient of the training loss using the implicit closed-form solution of the lower-level variational problem given by its dual problem, and provide an accompanying gradient descent algorithm (dubbed BLORC) to minimize the loss. Our experiments on simple natural images and for denoising 1D signals show that the proposed method can learn meaningful operators and the analytical gradients calculated are faster than standard automatic differentiation methods. While the approach we present is applied to denoising, we believe that it can be adapted to a wide-variety of inverse problems with linear measurement models, thus giving it applicability in a wide range of scenarios.