Madeline Mitchell
Learning Sparsity-Promoting Regularizers using Bilevel Optimization
Jul 18, 2022
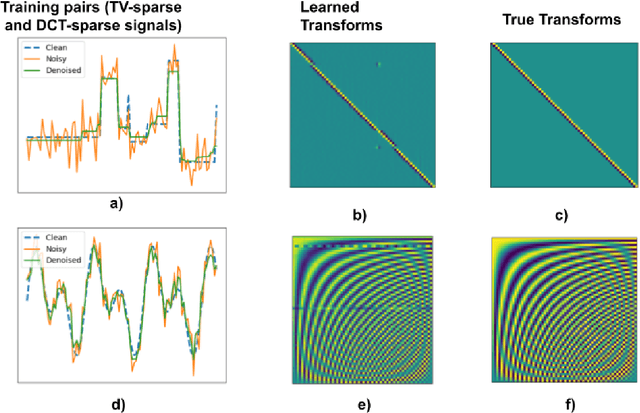

Abstract:We present a method for supervised learning of sparsity-promoting regularizers for denoising signals and images. Sparsity-promoting regularization is a key ingredient in solving modern signal reconstruction problems; however, the operators underlying these regularizers are usually either designed by hand or learned from data in an unsupervised way. The recent success of supervised learning (mainly convolutional neural networks) in solving image reconstruction problems suggests that it could be a fruitful approach to designing regularizers. Towards this end, we propose to denoise signals using a variational formulation with a parametric, sparsity-promoting regularizer, where the parameters of the regularizer are learned to minimize the mean squared error of reconstructions on a training set of ground truth image and measurement pairs. Training involves solving a challenging bilievel optimization problem; we derive an expression for the gradient of the training loss using the closed-form solution of the denoising problem and provide an accompanying gradient descent algorithm to minimize it. Our experiments with structured 1D signals and natural images show that the proposed method can learn an operator that outperforms well-known regularizers (total variation, DCT-sparsity, and unsupervised dictionary learning) and collaborative filtering for denoising. While the approach we present is specific to denoising, we believe that it could be adapted to the larger class of inverse problems with linear measurement models, giving it applicability in a wide range of signal reconstruction settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge