BLAST: Block-Level Adaptive Structured Matrices for Efficient Deep Neural Network Inference

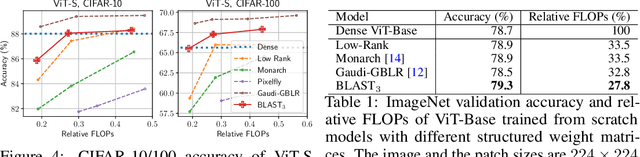
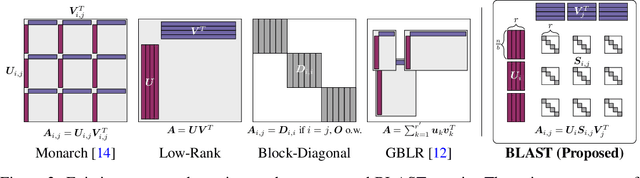
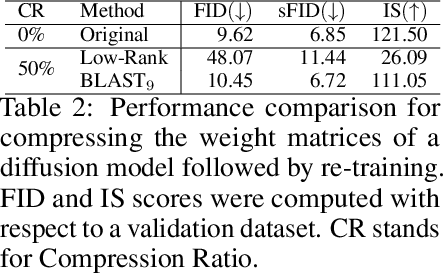
Large-scale foundation models have demonstrated exceptional performance in language and vision tasks. However, the numerous dense matrix-vector operations involved in these large networks pose significant computational challenges during inference. To address these challenges, we introduce the Block-Level Adaptive STructured (BLAST) matrix, designed to learn and leverage efficient structures prevalent in the weight matrices of linear layers within deep learning models. Compared to existing structured matrices, the BLAST matrix offers substantial flexibility, as it can represent various types of structures that are either learned from data or computed from pre-existing weight matrices. We demonstrate the efficiency of using the BLAST matrix for compressing both language and vision tasks, showing that (i) for medium-sized models such as ViT and GPT-2, training with BLAST weights boosts performance while reducing complexity by 70\% and 40\%, respectively; and (ii) for large foundation models such as Llama-7B and DiT-XL, the BLAST matrix achieves a 2x compression while exhibiting the lowest performance degradation among all tested structured matrices. Our code is available at \url{https://github.com/changwoolee/BLAST}.

Decoupled Data Consistency with Diffusion Purification for Image Restoration

Diffusion models have recently gained traction as a powerful class of deep generative priors, excelling in a wide range of image restoration tasks due to their exceptional ability to model data distributions. To solve image restoration problems, many existing techniques achieve data consistency by incorporating additional likelihood gradient steps into the reverse sampling process of diffusion models. However, the additional gradient steps pose a challenge for real-world practical applications as they incur a large computational overhead, thereby increasing inference time. They also present additional difficulties when using accelerated diffusion model samplers, as the number of data consistency steps is limited by the number of reverse sampling steps. In this work, we propose a novel diffusion-based image restoration solver that addresses these issues by decoupling the reverse process from the data consistency steps. Our method involves alternating between a reconstruction phase to maintain data consistency and a refinement phase that enforces the prior via diffusion purification. Our approach demonstrates versatility, making it highly adaptable for efficient problem-solving in latent space. Additionally, it reduces the necessity for numerous sampling steps through the integration of consistency models. The efficacy of our approach is validated through comprehensive experiments across various image restoration tasks, including image denoising, deblurring, inpainting, and super-resolution.

Efficient Compression of Overparameterized Deep Models through Low-Dimensional Learning Dynamics

Overparameterized models have proven to be powerful tools for solving various machine learning tasks. However, overparameterization often leads to a substantial increase in computational and memory costs, which in turn requires extensive resources to train. In this work, we aim to reduce this complexity by studying the learning dynamics of overparameterized deep networks. By extensively studying its learning dynamics, we unveil that the weight matrices of various architectures exhibit a low-dimensional structure. This finding implies that we can compress the networks by reducing the training to a small subspace. We take a step in developing a principled approach for compressing deep networks by studying deep linear models. We demonstrate that the principal components of deep linear models are fitted incrementally but within a small subspace, and use these insights to compress deep linear networks by decreasing the width of its intermediate layers. Remarkably, we observe that with a particular choice of initialization, the compressed network converges faster than the original network, consistently yielding smaller recovery errors throughout all iterations of gradient descent. We substantiate this observation by developing a theory focused on the deep matrix factorization problem, and by conducting empirical evaluations on deep matrix sensing. Finally, we demonstrate how our compressed model can enhance the utility of deep nonlinear models. Overall, we observe that our compression technique accelerates the training process by more than 2x, without compromising model quality.

Solving Inverse Problems with Latent Diffusion Models via Hard Data Consistency

Diffusion models have recently emerged as powerful generative priors for solving inverse problems. However, training diffusion models in the pixel space are both data intensive and computationally demanding, which restricts their applicability as priors in domains such as medical imaging. Latent diffusion models, which operate in a much lower-dimensional space, offer a solution to these challenges. Though, their direct application to solving inverse problems remains an unsolved technical challenge due to the nonlinearity of the encoder and decoder. To address this issue,we propose ReSample, an algorithm that solves general inverse problems with pre-trained latent diffusion models. Our algorithm incorporates data consistency by solving an optimization problem during the reverse sampling process, a concept that we term as hard data consistency. Upon solving this optimization problem, we propose a novel resampling scheme to map the measurement-consistent sample back onto the correct data manifold. Our approach offers both memory efficiency and considerable flexibility in the sense that (1) it can be readily adapted to various inverse problems using the same pre-trained model as it does not assume any fixed forward measurement operator during training, and (2) it can be generalized to different domains by simply fine-tuning the latent diffusion model with a minimal amount of data samples. Our empirical results on both linear and non-linear inverse problems demonstrate that our approach can reconstruct high-quality images even compared to state-of-the-art works that operate in the pixel space.

Low-Rank Phase Retrieval with Structured Tensor Models

We study the low-rank phase retrieval problem, where the objective is to recover a sequence of signals (typically images) given the magnitude of linear measurements of those signals. Existing solutions involve recovering a matrix constructed by vectorizing and stacking each image. These algorithms model this matrix to be low-rank and leverage the low-rank property to decrease the sample complexity required for accurate recovery. However, when the number of available measurements is more limited, these low-rank matrix models can often fail. We propose an algorithm called Tucker-Structured Phase Retrieval (TSPR) that models the sequence of images as a tensor rather than a matrix that we factorize using the Tucker decomposition. This factorization reduces the number of parameters that need to be estimated, allowing for a more accurate reconstruction in the under-sampled regime. Interestingly, we observe that this structure also has improved performance in the over-determined setting when the Tucker ranks are chosen appropriately. We demonstrate the effectiveness of our approach on real video datasets under several different measurement models.