Structure-Preserving Network Compression Via Low-Rank Induced Training Through Linear Layers Composition

Deep Neural Networks (DNNs) have achieved remarkable success in addressing many previously unsolvable tasks. However, the storage and computational requirements associated with DNNs pose a challenge for deploying these trained models on resource-limited devices. Therefore, a plethora of compression and pruning techniques have been proposed in recent years. Low-rank decomposition techniques are among the approaches most utilized to address this problem. Compared to post-training compression, compression-promoted training is still under-explored. In this paper, we present a theoretically-justified novel approach, termed Low-Rank Induced Training (LoRITa), that promotes low-rankness through the composition of linear layers and compresses by using singular value truncation. This is achieved without the need to change the structure at inference time or require constrained and/or additional optimization, other than the standard weight decay regularization. Moreover, LoRITa eliminates the need to (i) initialize with pre-trained models and (ii) specify rank selection prior to training. Our experimental results (i) demonstrate the effectiveness of our approach using MNIST on Fully Connected Networks, CIFAR10 on Vision Transformers, and CIFAR10/100 on Convolutional Neural Networks, and (ii) illustrate that we achieve either competitive or SOTA results when compared to leading structured pruning methods in terms of FLOPs and parameters drop.

Decoupled Data Consistency with Diffusion Purification for Image Restoration

Diffusion models have recently gained traction as a powerful class of deep generative priors, excelling in a wide range of image restoration tasks due to their exceptional ability to model data distributions. To solve image restoration problems, many existing techniques achieve data consistency by incorporating additional likelihood gradient steps into the reverse sampling process of diffusion models. However, the additional gradient steps pose a challenge for real-world practical applications as they incur a large computational overhead, thereby increasing inference time. They also present additional difficulties when using accelerated diffusion model samplers, as the number of data consistency steps is limited by the number of reverse sampling steps. In this work, we propose a novel diffusion-based image restoration solver that addresses these issues by decoupling the reverse process from the data consistency steps. Our method involves alternating between a reconstruction phase to maintain data consistency and a refinement phase that enforces the prior via diffusion purification. Our approach demonstrates versatility, making it highly adaptable for efficient problem-solving in latent space. Additionally, it reduces the necessity for numerous sampling steps through the integration of consistency models. The efficacy of our approach is validated through comprehensive experiments across various image restoration tasks, including image denoising, deblurring, inpainting, and super-resolution.

A Differentiable Approach to Combinatorial Optimization using Dataless Neural Networks

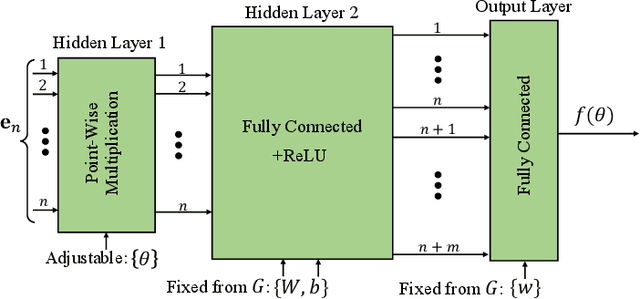
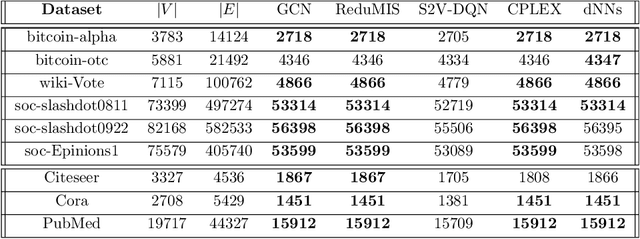
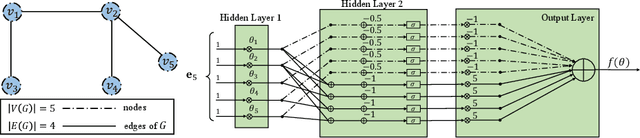
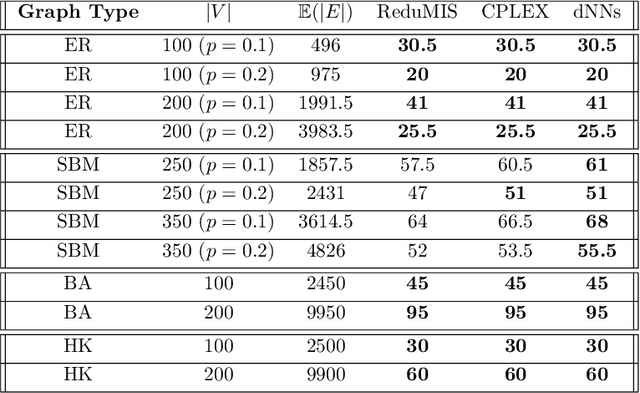
The success of machine learning solutions for reasoning about discrete structures has brought attention to its adoption within combinatorial optimization algorithms. Such approaches generally rely on supervised learning by leveraging datasets of the combinatorial structures of interest drawn from some distribution of problem instances. Reinforcement learning has also been employed to find such structures. In this paper, we propose a radically different approach in that no data is required for training the neural networks that produce the solution. In particular, we reduce the combinatorial optimization problem to a neural network and employ a dataless training scheme to refine the parameters of the network such that those parameters yield the structure of interest. We consider the combinatorial optimization problems of finding maximum independent sets and maximum cliques in a graph. In principle, since these problems belong to the NP-hard complexity class, our proposed approach can be used to solve any other NP-hard problem. Additionally, we propose a universal graph reduction procedure to handle large scale graphs. The reduction exploits community detection for graph partitioning and is applicable to any graph type and/or density. Experimental evaluation on both synthetic graphs and real-world benchmarks demonstrates that our method performs on par with or outperforms state-of-the-art heuristic, reinforcement learning, and machine learning based methods without requiring any data.