A Differentiable Approach to Combinatorial Optimization using Dataless Neural Networks
Paper and Code
Mar 15, 2022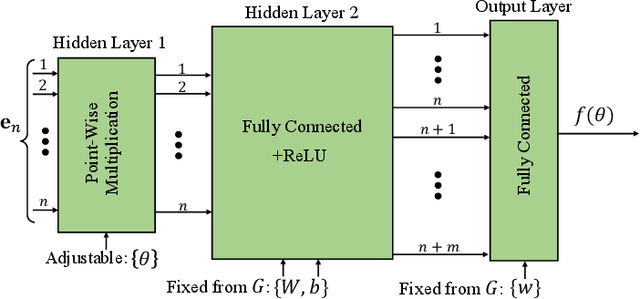
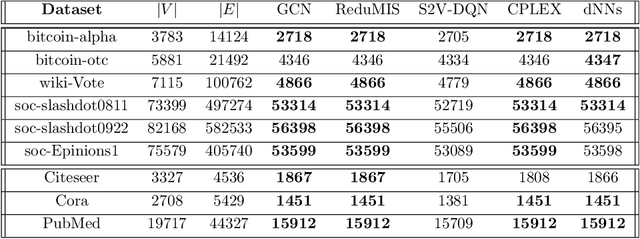
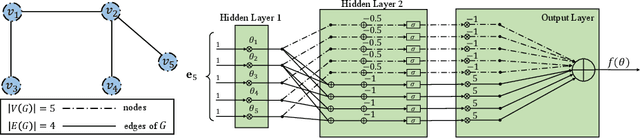
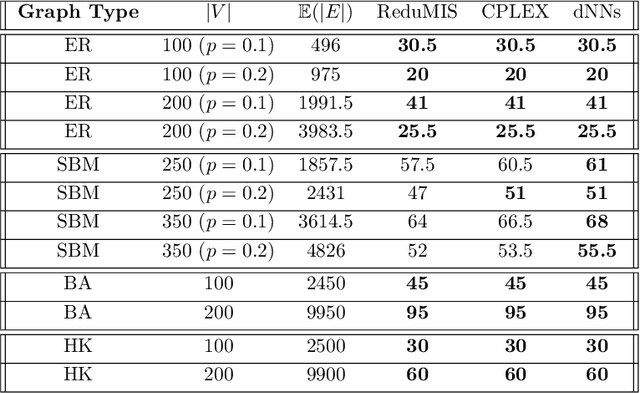
The success of machine learning solutions for reasoning about discrete structures has brought attention to its adoption within combinatorial optimization algorithms. Such approaches generally rely on supervised learning by leveraging datasets of the combinatorial structures of interest drawn from some distribution of problem instances. Reinforcement learning has also been employed to find such structures. In this paper, we propose a radically different approach in that no data is required for training the neural networks that produce the solution. In particular, we reduce the combinatorial optimization problem to a neural network and employ a dataless training scheme to refine the parameters of the network such that those parameters yield the structure of interest. We consider the combinatorial optimization problems of finding maximum independent sets and maximum cliques in a graph. In principle, since these problems belong to the NP-hard complexity class, our proposed approach can be used to solve any other NP-hard problem. Additionally, we propose a universal graph reduction procedure to handle large scale graphs. The reduction exploits community detection for graph partitioning and is applicable to any graph type and/or density. Experimental evaluation on both synthetic graphs and real-world benchmarks demonstrates that our method performs on par with or outperforms state-of-the-art heuristic, reinforcement learning, and machine learning based methods without requiring any data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge