Scalable and Robust Tensor Ring Decomposition for Large-scale Data

Tensor ring (TR) decomposition has recently received increased attention due to its superior expressive performance for high-order tensors. However, the applicability of traditional TR decomposition algorithms to real-world applications is hindered by prevalent large data sizes, missing entries, and corruption with outliers. In this work, we propose a scalable and robust TR decomposition algorithm capable of handling large-scale tensor data with missing entries and gross corruptions. We first develop a novel auto-weighted steepest descent method that can adaptively fill the missing entries and identify the outliers during the decomposition process. Further, taking advantage of the tensor ring model, we develop a novel fast Gram matrix computation (FGMC) approach and a randomized subtensor sketching (RStS) strategy which yield significant reduction in storage and computational complexity. Experimental results demonstrate that the proposed method outperforms existing TR decomposition methods in the presence of outliers, and runs significantly faster than existing robust tensor completion algorithms.

Distributionally Robust Domain Adaptation

Domain Adaptation (DA) has recently received significant attention due to its potential to adapt a learning model across source and target domains with mismatched distributions. Since DA methods rely exclusively on the given source and target domain samples, they generally yield models that are vulnerable to noise and unable to adapt to unseen samples from the target domain, which calls for DA methods that guarantee the robustness and generalization of the learned models. In this paper, we propose DRDA, a distributionally robust domain adaptation method. DRDA leverages a distributionally robust optimization (DRO) framework to learn a robust decision function that minimizes the worst-case target domain risk and generalizes to any sample from the target domain by transferring knowledge from a given labeled source domain sample. We utilize the Maximum Mean Discrepancy (MMD) metric to construct an ambiguity set of distributions that provably contains the source and target domain distributions with high probability. Hence, the risk is shown to upper bound the out-of-sample target domain loss. Our experimental results demonstrate that our formulation outperforms existing robust learning approaches.

A Differentiable Approach to Combinatorial Optimization using Dataless Neural Networks

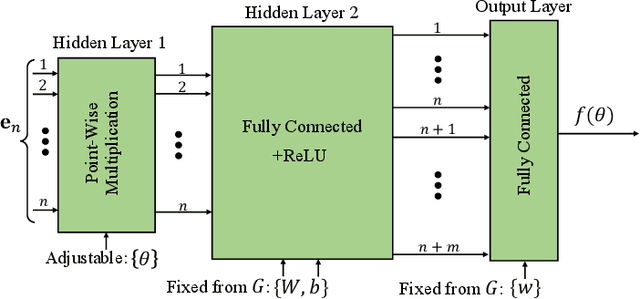
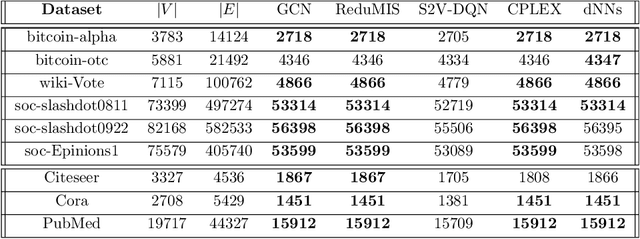
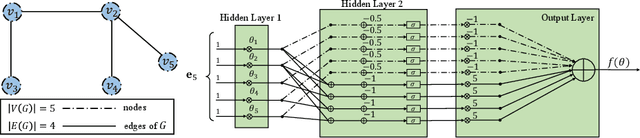
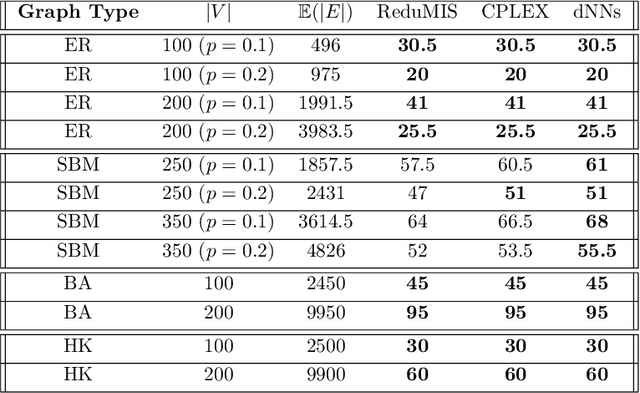
The success of machine learning solutions for reasoning about discrete structures has brought attention to its adoption within combinatorial optimization algorithms. Such approaches generally rely on supervised learning by leveraging datasets of the combinatorial structures of interest drawn from some distribution of problem instances. Reinforcement learning has also been employed to find such structures. In this paper, we propose a radically different approach in that no data is required for training the neural networks that produce the solution. In particular, we reduce the combinatorial optimization problem to a neural network and employ a dataless training scheme to refine the parameters of the network such that those parameters yield the structure of interest. We consider the combinatorial optimization problems of finding maximum independent sets and maximum cliques in a graph. In principle, since these problems belong to the NP-hard complexity class, our proposed approach can be used to solve any other NP-hard problem. Additionally, we propose a universal graph reduction procedure to handle large scale graphs. The reduction exploits community detection for graph partitioning and is applicable to any graph type and/or density. Experimental evaluation on both synthetic graphs and real-world benchmarks demonstrates that our method performs on par with or outperforms state-of-the-art heuristic, reinforcement learning, and machine learning based methods without requiring any data.

Support Recovery Guarantees for Periodic Signals with Nested Periodic Dictionaries

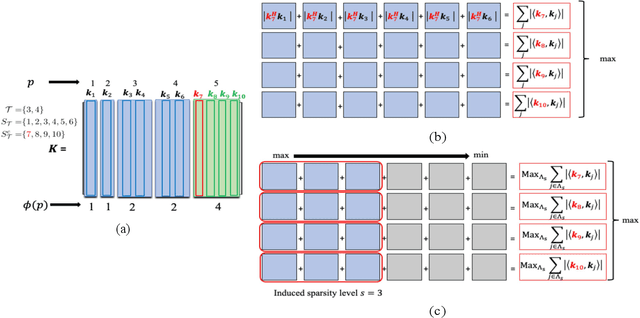
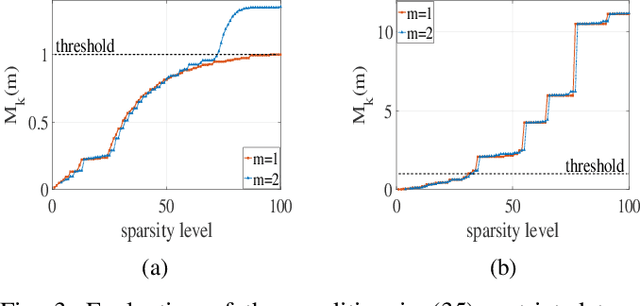
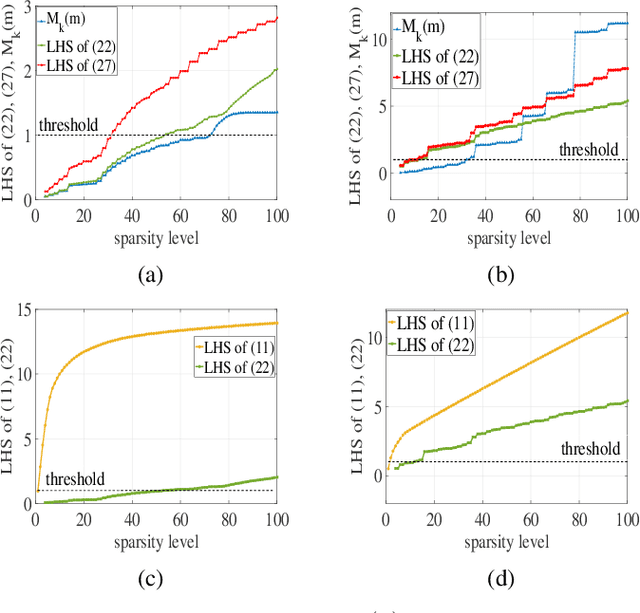
Periodic signals composed of periodic mixtures admit sparse representations in nested periodic dictionaries (NPDs). Therefore, their underlying hidden periods can be estimated by recovering the exact support of said representations. In this paper, support recovery guarantees of such signals are derived both in noise-free and noisy settings. While exact recovery conditions have long been studied in the theory of compressive sensing, existing conditions fall short of yielding meaningful achievability regions in the context of periodic signals with sparse representations in NPDs, in part since existing bounds do not capture structures intrinsic to these dictionaries. We leverage known properties of NPDs to derive several conditions for exact sparse recovery of periodic mixtures in the noise-free setting. These conditions rest on newly introduced notions of nested periodic coherence and restricted coherence, which can be efficiently computed and verified. In the presence of noise, we obtain improved conditions for recovering the exact support set of the sparse representation of the periodic mixture via orthogonal matching pursuit based on the introduced notions of coherence. The theoretical findings are corroborated using numerical experiments for different families of NPDs. Our results show significant improvement over generic recovery bounds as the conditions hold over a larger range of sparsity levels.

Robust M-estimation-based Tensor Ring Completion: a Half-quadratic Minimization Approach

Tensor completion is the problem of estimating the missing values of high-order data from partially observed entries. Among several definitions of tensor rank, tensor ring rank affords the flexibility and accuracy needed to model tensors of different orders, which motivated recent efforts on tensor-ring completion. However, data corruption due to prevailing outliers poses major challenges to existing algorithms. In this paper, we develop a robust approach to tensor ring completion that uses an M-estimator as its error statistic, which can significantly alleviate the effect of outliers. Leveraging a half-quadratic (HQ) method, we reformulate the problem as one of weighted tensor completion. We present two HQ-based algorithms based on truncated singular value decomposition and matrix factorization along with their convergence and complexity analysis. Extendibility of the proposed approach to alternative definitions of tensor rank is also discussed. The experimental results demonstrate the superior performance of the proposed approach over state-of-the-art robust algorithms for tensor completion.

Non-local Patch-based Low-rank Tensor Ring Completion for Visual Data

Tensor completion is the problem of estimating the missing entries of a partially observed tensor with a certain low-rank structure. It improves on matrix completion for image and video data by capturing additional structural information intrinsic to such data. % With more inherent information involving in tensor structure than matrix, tensor completion has shown better performance compared with matrix completion especially in image and video data. Traditional completion algorithms treat the entire visual data as a tensor, which may not always work well especially when camera or object motion exists. In this paper, we develop a novel non-local patch-based tensor ring completion algorithm. In the proposed approach, similar patches are extracted for each reference patch along both the spatial and temporal domains of the visual data. The collected patches are then formed into a high-order tensor and a tensor ring completion algorithm is proposed to recover the completed tensor. A novel interval sampling-based block matching (ISBM) strategy and a hybrid completion strategy are also proposed to improve efficiency and accuracy. Further, we develop an online patch-based completion algorithm to deal with streaming video data. An efficient online tensor ring completion algorithm is proposed to reduce the time cost. Extensive experimental results demonstrate the superior performance of the proposed algorithms compared with state-of-the-art methods.

Verifiable Planning in Expected Reward Multichain MDPs

The planning domain has experienced increased interest in the formal synthesis of decision-making policies. This formal synthesis typically entails finding a policy which satisfies formal specifications in the form of some well-defined logic, such as Linear Temporal Logic (LTL) or Computation Tree Logic (CTL), among others. While such logics are very powerful and expressive in their capacity to capture desirable agent behavior, their value is limited when deriving decision-making policies which satisfy certain types of asymptotic behavior. In particular, we are interested in specifying constraints on the steady-state behavior of an agent, which captures the proportion of time an agent spends in each state as it interacts for an indefinite period of time with its environment. This is sometimes called the average or expected behavior of the agent. In this paper, we explore the steady-state planning problem of deriving a decision-making policy for an agent such that constraints on its steady-state behavior are satisfied. A linear programming solution for the general case of multichain Markov Decision Processes (MDPs) is proposed and we prove that optimal solutions to the proposed programs yield stationary policies with rigorous guarantees of behavior.

Robust Low-tubal-rank Tensor Completion based on Tensor Factorization and Maximum Correntopy Criterion

The goal of tensor completion is to recover a tensor from a subset of its entries, often by exploiting its low-rank property. Among several useful definitions of tensor rank, the low-tubal-rank was shown to give a valuable characterization of the inherent low-rank structure of a tensor. While some low-tubal-rank tensor completion algorithms with favorable performance have been recently proposed, these algorithms utilize second-order statistics to measure the error residual, which may not work well when the observed entries contain large outliers. In this paper, we propose a new objective function for low-tubal-rank tensor completion, which uses correntropy as the error measure to mitigate the effect of the outliers. To efficiently optimize the proposed objective, we leverage a half-quadratic minimization technique whereby the optimization is transformed to a weighted low-tubal-rank tensor factorization problem. Subsequently, we propose two simple and efficient algorithms to obtain the solution and provide their convergence and complexity analysis. Numerical results using both synthetic and real data demonstrate the robust and superior performance of the proposed algorithms.

Sketch-based community detection in evolving networks

We consider an approach for community detection in time-varying networks. At its core, this approach maintains a small sketch graph to capture the essential community structure found in each snapshot of the full network. We demonstrate how the sketch can be used to explicitly identify six key community events which typically occur during network evolution: growth, shrinkage, merging, splitting, birth and death. Based on these detection techniques, we formulate a community detection algorithm which can process a network concurrently exhibiting all processes. One advantage afforded by the sketch-based algorithm is the efficient handling of large networks. Whereas detecting events in the full graph may be computationally expensive, the small size of the sketch allows changes to be quickly assessed. A second advantage occurs in networks containing clusters of disproportionate size. The sketch is constructed such that there is equal representation of each cluster, thus reducing the possibility that the small clusters are lost in the estimate. We present a new standardized benchmark based on the stochastic block model which models the addition and deletion of nodes, as well as the birth and death of communities. When coupled with existing benchmarks, this new benchmark provides a comprehensive suite of tests encompassing all six community events. We provide a set of numerical results demonstrating the advantages of our approach both in run time and in the handling of small clusters.

Multi-modal Non-line-of-sight Passive Imaging

We consider the non-line-of-sight (NLOS) imaging of an object using light reflected off a diffusive wall. The wall scatters incident light such that a lens is no longer useful to form an image. Instead, we exploit the four-dimensional spatial coherence function to reconstruct a two-dimensional projection of the obscured object. The approach is completely passive in the sense that no control over the light illuminating the object is assumed, and is compatible with the partially coherent fields ubiquitous in both indoor and outdoor environments. We formulate a multi-criteria convex optimization problem for reconstruction, which fuses reflected field's intensity and spatial coherence information at different scales. Our formulation leverages established optics models of light propagation and scattering and exploits the sparsity common to many images in different bases. We also develop an algorithm based on the Alternating Direction Method of Multipliers to efficiently solve the convex program proposed. A means for analyzing the null space of the measurement matrices is provided, as well as a means for weighing the contribution of individual measurements to the reconstruction. This work holds promise to advance passive imaging in challenging NLOS regimes in which the intensity does not necessarily retain distinguishable features, and provides a framework for multi-modal information fusion for efficient scene reconstruction.