Unraveling overoptimism and publication bias in ML-driven science

Machine Learning (ML) is increasingly used across many disciplines with impressive reported results across many domain areas. However, recent studies suggest that the published performance of ML models are often overoptimistic and not reflective of true accuracy were these models to be deployed. Validity concerns are underscored by findings of a concerning inverse relationship between sample size and reported accuracy in published ML models across several domains. This is in contrast with the theory of learning curves in ML, where we expect accuracy to improve or stay the same with increasing sample size. This paper investigates the factors contributing to overoptimistic accuracy reports in ML-based science, focusing on data leakage and publication bias. Our study introduces a novel stochastic model for observed accuracy, integrating parametric learning curves and the above biases. We then construct an estimator based on this model that corrects for these biases in observed data. Theoretical and empirical results demonstrate that this framework can estimate the underlying learning curve that gives rise to the observed overoptimistic results, thereby providing more realistic performance assessments of ML performance from a collection of published results. We apply the model to various meta-analyses in the digital health literature, including neuroimaging-based and speech-based classifications of several neurological conditions. Our results indicate prevalent overoptimism across these fields and we estimate the inherent limits of ML-based prediction in each domain.

Active Sequential Two-Sample Testing

Two-sample testing tests whether the distributions generating two samples are identical. We pose the two-sample testing problem in a new scenario where the sample measurements (or sample features) are inexpensive to access, but their group memberships (or labels) are costly. We devise the first \emph{active sequential two-sample testing framework} that not only sequentially but also \emph{actively queries} sample labels to address the problem. Our test statistic is a likelihood ratio where one likelihood is found by maximization over all class priors, and the other is given by a classification model. The classification model is adaptively updated and then used to guide an active query scheme called bimodal query to label sample features in the regions with high dependency between the feature variables and the label variables. The theoretical contributions in the paper include proof that our framework produces an \emph{anytime-valid} $p$-value; and, under reachable conditions and a mild assumption, the framework asymptotically generates a minimum normalized log-likelihood ratio statistic that a passive query scheme can only achieve when the feature variable and the label variable have the highest dependence. Lastly, we provide a \emph{query-switching (QS)} algorithm to decide when to switch from passive query to active query and adapt bimodal query to increase the testing power of our test. Extensive experiments justify our theoretical contributions and the effectiveness of QS.

Support Recovery Guarantees for Periodic Signals with Nested Periodic Dictionaries

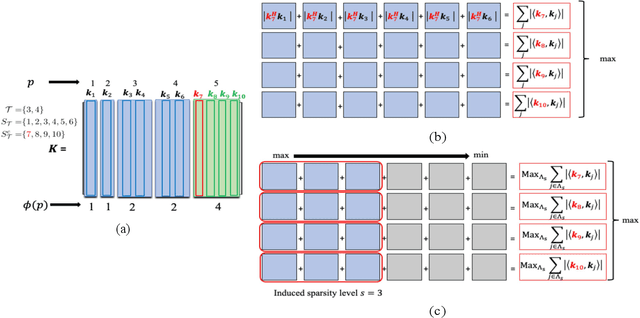
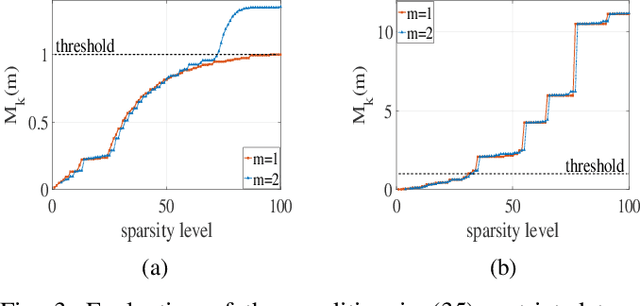
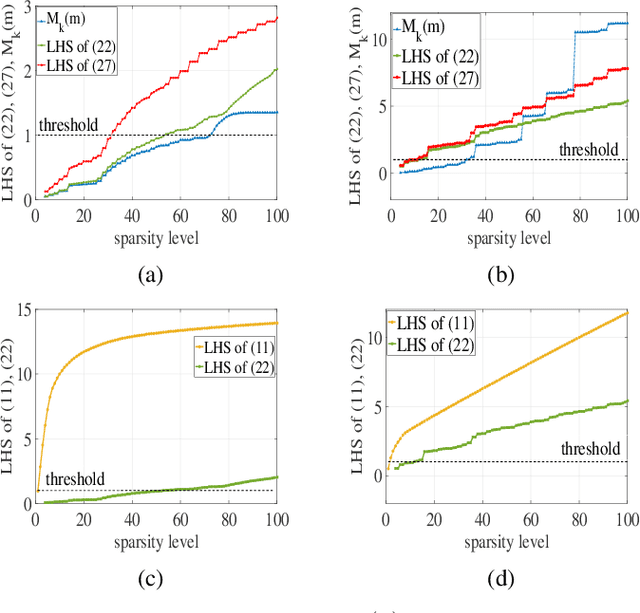
Periodic signals composed of periodic mixtures admit sparse representations in nested periodic dictionaries (NPDs). Therefore, their underlying hidden periods can be estimated by recovering the exact support of said representations. In this paper, support recovery guarantees of such signals are derived both in noise-free and noisy settings. While exact recovery conditions have long been studied in the theory of compressive sensing, existing conditions fall short of yielding meaningful achievability regions in the context of periodic signals with sparse representations in NPDs, in part since existing bounds do not capture structures intrinsic to these dictionaries. We leverage known properties of NPDs to derive several conditions for exact sparse recovery of periodic mixtures in the noise-free setting. These conditions rest on newly introduced notions of nested periodic coherence and restricted coherence, which can be efficiently computed and verified. In the presence of noise, we obtain improved conditions for recovering the exact support set of the sparse representation of the periodic mixture via orthogonal matching pursuit based on the introduced notions of coherence. The theoretical findings are corroborated using numerical experiments for different families of NPDs. Our results show significant improvement over generic recovery bounds as the conditions hold over a larger range of sparsity levels.