Support Recovery Guarantees for Periodic Signals with Nested Periodic Dictionaries
Paper and Code
Oct 25, 2021
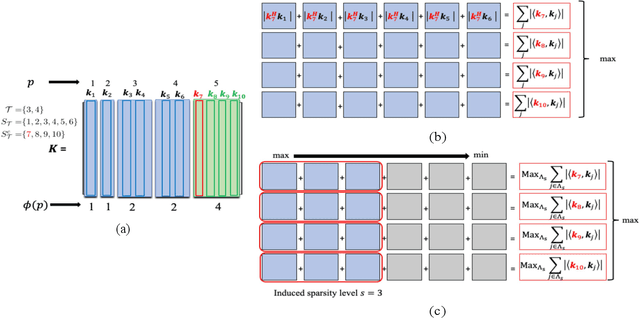
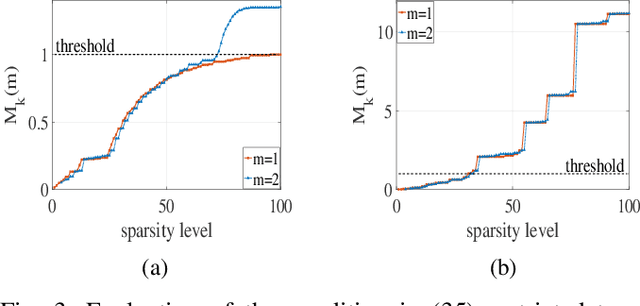
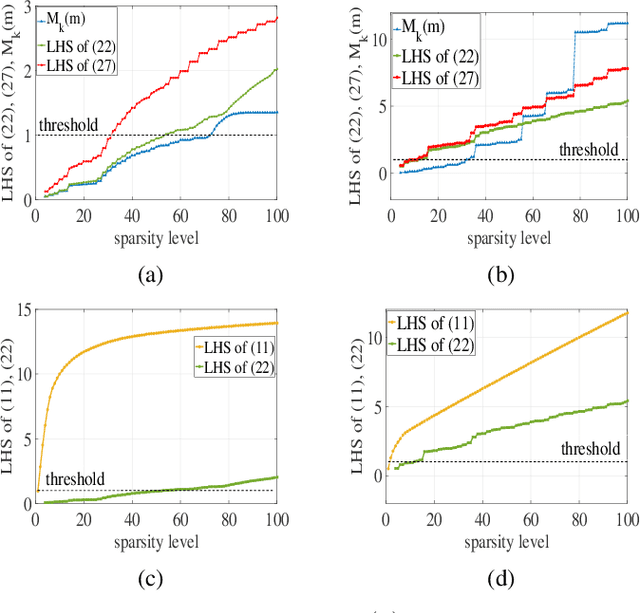
Periodic signals composed of periodic mixtures admit sparse representations in nested periodic dictionaries (NPDs). Therefore, their underlying hidden periods can be estimated by recovering the exact support of said representations. In this paper, support recovery guarantees of such signals are derived both in noise-free and noisy settings. While exact recovery conditions have long been studied in the theory of compressive sensing, existing conditions fall short of yielding meaningful achievability regions in the context of periodic signals with sparse representations in NPDs, in part since existing bounds do not capture structures intrinsic to these dictionaries. We leverage known properties of NPDs to derive several conditions for exact sparse recovery of periodic mixtures in the noise-free setting. These conditions rest on newly introduced notions of nested periodic coherence and restricted coherence, which can be efficiently computed and verified. In the presence of noise, we obtain improved conditions for recovering the exact support set of the sparse representation of the periodic mixture via orthogonal matching pursuit based on the introduced notions of coherence. The theoretical findings are corroborated using numerical experiments for different families of NPDs. Our results show significant improvement over generic recovery bounds as the conditions hold over a larger range of sparsity levels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge