Airlift Challenge: A Competition for Optimizing Cargo Delivery

Airlift operations require the timely distribution of various cargo, much of which is time sensitive and valuable. However, these operations have to contend with sudden disruptions from weather and malfunctions, requiring immediate rescheduling. The Airlift Challenge competition seeks possible solutions via a simulator that provides a simplified abstraction of the airlift problem. The simulator uses an OpenAI gym interface that allows participants to create an algorithm for planning agent actions. The algorithm is scored using a remote evaluator against scenarios of ever-increasing difficulty. The second iteration of the competition was underway from November 2023 to April 2024. In this paper, we describe the competition and simulation environment. As a step towards applying generalized planning techniques to the problem, we present a temporal PDDL domain for the Pickup and Delivery Problem, a model which lies at the core of the Airlift Challenge.

Automaton Distillation: Neuro-Symbolic Transfer Learning for Deep Reinforcement Learning

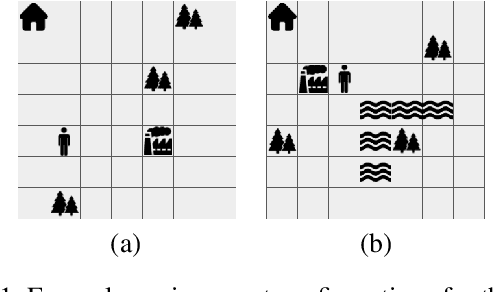
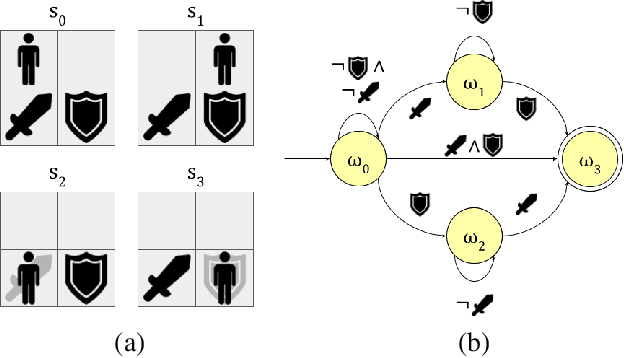
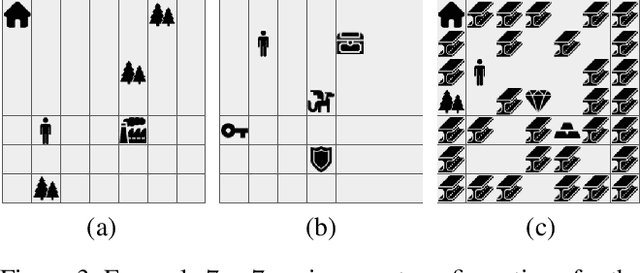
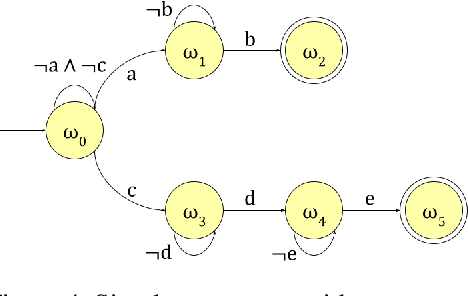
Reinforcement learning (RL) is a powerful tool for finding optimal policies in sequential decision processes. However, deep RL methods suffer from two weaknesses: collecting the amount of agent experience required for practical RL problems is prohibitively expensive, and the learned policies exhibit poor generalization on tasks outside of the training distribution. To mitigate these issues, we introduce automaton distillation, a form of neuro-symbolic transfer learning in which Q-value estimates from a teacher are distilled into a low-dimensional representation in the form of an automaton. We then propose two methods for generating Q-value estimates: static transfer, which reasons over an abstract Markov Decision Process constructed based on prior knowledge, and dynamic transfer, where symbolic information is extracted from a teacher Deep Q-Network (DQN). The resulting Q-value estimates from either method are used to bootstrap learning in the target environment via a modified DQN loss function. We list several failure modes of existing automaton-based transfer methods and demonstrate that both static and dynamic automaton distillation decrease the time required to find optimal policies for various decision tasks.

On the Robustness of AlphaFold: A COVID-19 Case Study

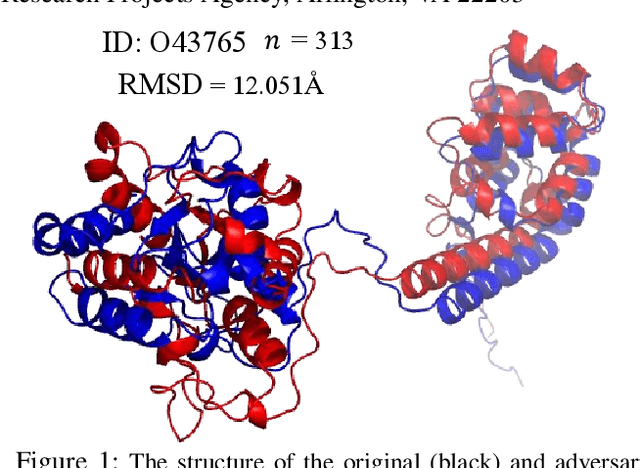
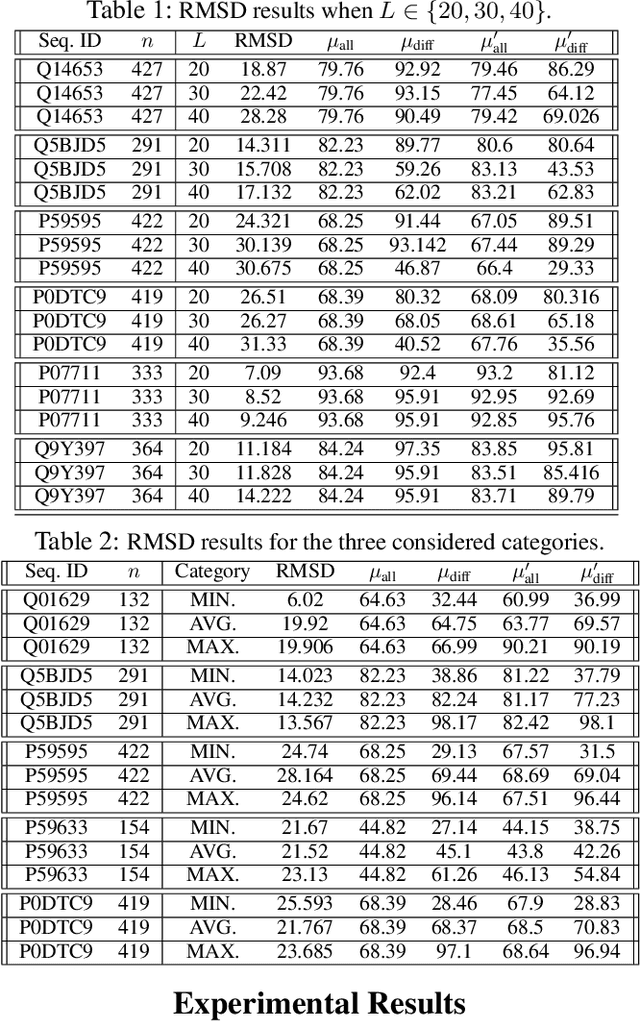
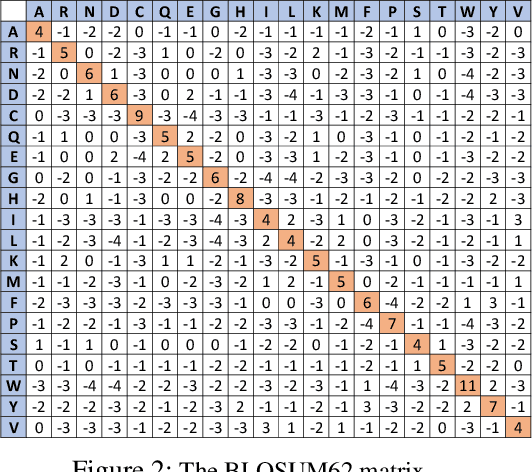
Protein folding neural networks (PFNNs) such as AlphaFold predict remarkably accurate structures of proteins compared to other approaches. However, the robustness of such networks has heretofore not been explored. This is particularly relevant given the broad social implications of such technologies and the fact that biologically small perturbations in the protein sequence do not generally lead to drastic changes in the protein structure. In this paper, we demonstrate that AlphaFold does not exhibit such robustness despite its high accuracy. This raises the challenge of detecting and quantifying the extent to which these predicted protein structures can be trusted. To measure the robustness of the predicted structures, we utilize (i) the root-mean-square deviation (RMSD) and (ii) the Global Distance Test (GDT) similarity measure between the predicted structure of the original sequence and the structure of its adversarially perturbed version. We prove that the problem of minimally perturbing protein sequences to fool protein folding neural networks is NP-complete. Based on the well-established BLOSUM62 sequence alignment scoring matrix, we generate adversarial protein sequences and show that the RMSD between the predicted protein structure and the structure of the original sequence are very large when the adversarial changes are bounded by (i) 20 units in the BLOSUM62 distance, and (ii) five residues (out of hundreds or thousands of residues) in the given protein sequence. In our experimental evaluation, we consider 111 COVID-19 proteins in the Universal Protein resource (UniProt), a central resource for protein data managed by the European Bioinformatics Institute, Swiss Institute of Bioinformatics, and the US Protein Information Resource. These result in an overall GDT similarity test score average of around 34%, demonstrating a substantial drop in the performance of AlphaFold.

Learning Probabilistic Reward Machines from Non-Markovian Stochastic Reward Processes

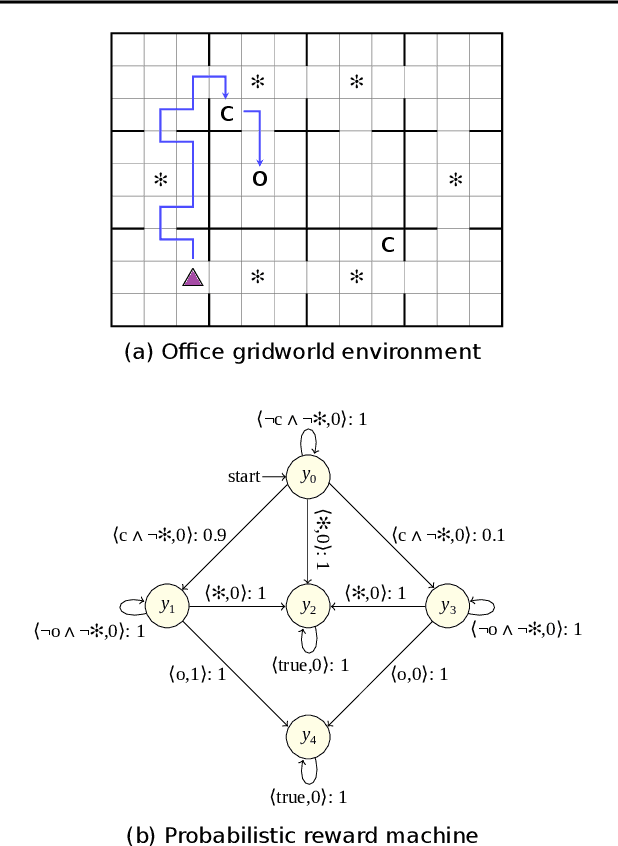
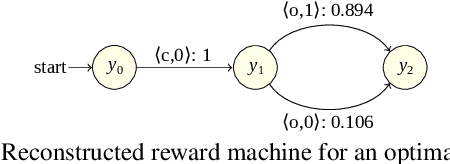
The success of reinforcement learning in typical settings is, in part, predicated on underlying Markovian assumptions on the reward signal by which an agent learns optimal policies. In recent years, the use of reward machines has relaxed this assumption by enabling a structured representation of non-Markovian rewards. In particular, such representations can be used to augment the state space of the underlying decision process, thereby facilitating non-Markovian reinforcement learning. However, these reward machines cannot capture the semantics of stochastic reward signals. In this paper, we make progress on this front by introducing probabilistic reward machines (PRMs) as a representation of non-Markovian stochastic rewards. We present an algorithm to learn PRMs from the underlying decision process as well as to learn the PRM representation of a given decision-making policy.

Controller Synthesis for Omega-Regular and Steady-State Specifications

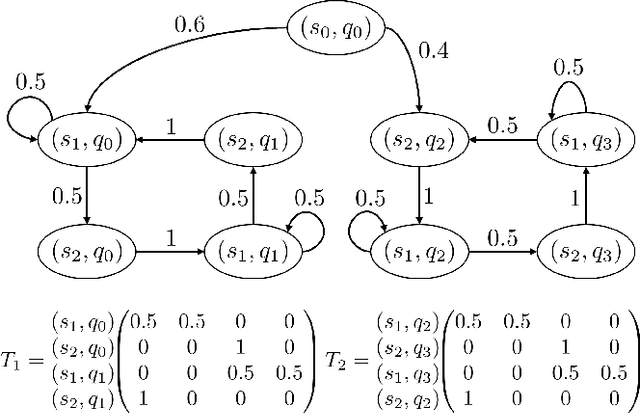
Given a Markov decision process (MDP) and a linear-time ($\omega$-regular or LTL) specification, the controller synthesis problem aims to compute the optimal policy that satisfies the specification. More recently, problems that reason over the asymptotic behavior of systems have been proposed through the lens of steady-state planning. This entails finding a control policy for an MDP such that the Markov chain induced by the solution policy satisfies a given set of constraints on its steady-state distribution. This paper studies a generalization of the controller synthesis problem for a linear-time specification under steady-state constraints on the asymptotic behavior. We present an algorithm to find a deterministic policy satisfying $\omega$-regular and steady-state constraints by characterizing the solutions as an integer linear program, and experimentally evaluate our approach.

Verifiable Planning in Expected Reward Multichain MDPs

The planning domain has experienced increased interest in the formal synthesis of decision-making policies. This formal synthesis typically entails finding a policy which satisfies formal specifications in the form of some well-defined logic, such as Linear Temporal Logic (LTL) or Computation Tree Logic (CTL), among others. While such logics are very powerful and expressive in their capacity to capture desirable agent behavior, their value is limited when deriving decision-making policies which satisfy certain types of asymptotic behavior. In particular, we are interested in specifying constraints on the steady-state behavior of an agent, which captures the proportion of time an agent spends in each state as it interacts for an indefinite period of time with its environment. This is sometimes called the average or expected behavior of the agent. In this paper, we explore the steady-state planning problem of deriving a decision-making policy for an agent such that constraints on its steady-state behavior are satisfied. A linear programming solution for the general case of multichain Markov Decision Processes (MDPs) is proposed and we prove that optimal solutions to the proposed programs yield stationary policies with rigorous guarantees of behavior.

Sketch-based community detection in evolving networks

We consider an approach for community detection in time-varying networks. At its core, this approach maintains a small sketch graph to capture the essential community structure found in each snapshot of the full network. We demonstrate how the sketch can be used to explicitly identify six key community events which typically occur during network evolution: growth, shrinkage, merging, splitting, birth and death. Based on these detection techniques, we formulate a community detection algorithm which can process a network concurrently exhibiting all processes. One advantage afforded by the sketch-based algorithm is the efficient handling of large networks. Whereas detecting events in the full graph may be computationally expensive, the small size of the sketch allows changes to be quickly assessed. A second advantage occurs in networks containing clusters of disproportionate size. The sketch is constructed such that there is equal representation of each cluster, thus reducing the possibility that the small clusters are lost in the estimate. We present a new standardized benchmark based on the stochastic block model which models the addition and deletion of nodes, as well as the birth and death of communities. When coupled with existing benchmarks, this new benchmark provides a comprehensive suite of tests encompassing all six community events. We provide a set of numerical results demonstrating the advantages of our approach both in run time and in the handling of small clusters.

Multi-modal Non-line-of-sight Passive Imaging

We consider the non-line-of-sight (NLOS) imaging of an object using light reflected off a diffusive wall. The wall scatters incident light such that a lens is no longer useful to form an image. Instead, we exploit the four-dimensional spatial coherence function to reconstruct a two-dimensional projection of the obscured object. The approach is completely passive in the sense that no control over the light illuminating the object is assumed, and is compatible with the partially coherent fields ubiquitous in both indoor and outdoor environments. We formulate a multi-criteria convex optimization problem for reconstruction, which fuses reflected field's intensity and spatial coherence information at different scales. Our formulation leverages established optics models of light propagation and scattering and exploits the sparsity common to many images in different bases. We also develop an algorithm based on the Alternating Direction Method of Multipliers to efficiently solve the convex program proposed. A means for analyzing the null space of the measurement matrices is provided, as well as a means for weighing the contribution of individual measurements to the reconstruction. This work holds promise to advance passive imaging in challenging NLOS regimes in which the intensity does not necessarily retain distinguishable features, and provides a framework for multi-modal information fusion for efficient scene reconstruction.

Randomized Robust Matrix Completion for the Community Detection Problem

This paper focuses on the unsupervised clustering of large partially observed graphs. We propose a provable randomized framework in which a clustering algorithm is applied to a graphs adjacency matrix generated from a stochastic block model. A sub-matrix is constructed using random sampling, and the low rank component is found using a convex-optimization based matrix completion algorithm. The clusters are then identified based on this low rank component using a correlation based retrieval step. Additionally, a new random node sampling algorithm is presented which significantly improves upon the performance of the clustering algorithm with unbalanced data. Given a partially observed graph with adjacency matrix A \in R^{N \times N} , the proposed approach can reduce the computational complexity from O(N^2) to O(N).