Automaton Distillation: Neuro-Symbolic Transfer Learning for Deep Reinforcement Learning

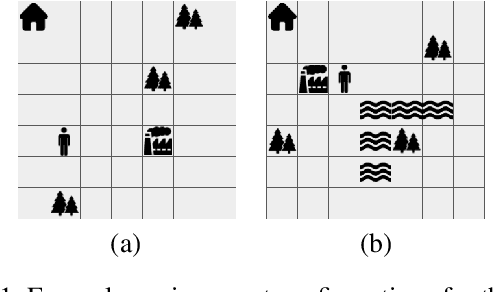
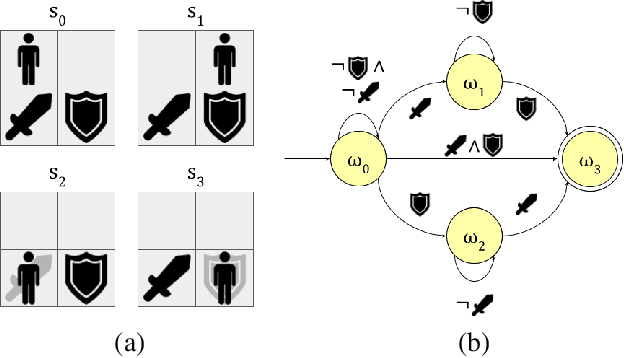
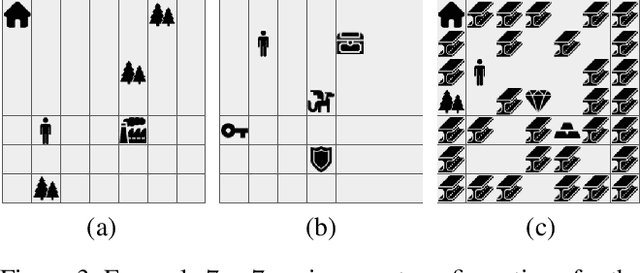
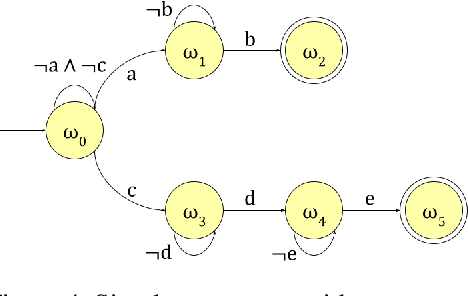
Reinforcement learning (RL) is a powerful tool for finding optimal policies in sequential decision processes. However, deep RL methods suffer from two weaknesses: collecting the amount of agent experience required for practical RL problems is prohibitively expensive, and the learned policies exhibit poor generalization on tasks outside of the training distribution. To mitigate these issues, we introduce automaton distillation, a form of neuro-symbolic transfer learning in which Q-value estimates from a teacher are distilled into a low-dimensional representation in the form of an automaton. We then propose two methods for generating Q-value estimates: static transfer, which reasons over an abstract Markov Decision Process constructed based on prior knowledge, and dynamic transfer, where symbolic information is extracted from a teacher Deep Q-Network (DQN). The resulting Q-value estimates from either method are used to bootstrap learning in the target environment via a modified DQN loss function. We list several failure modes of existing automaton-based transfer methods and demonstrate that both static and dynamic automaton distillation decrease the time required to find optimal policies for various decision tasks.

Model-Free Robust Average-Reward Reinforcement Learning

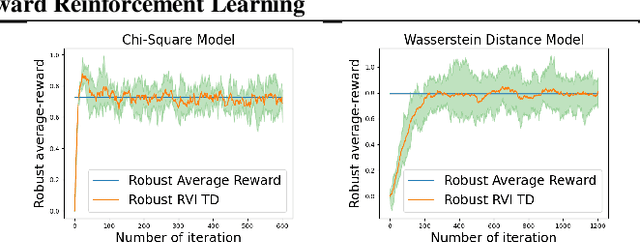
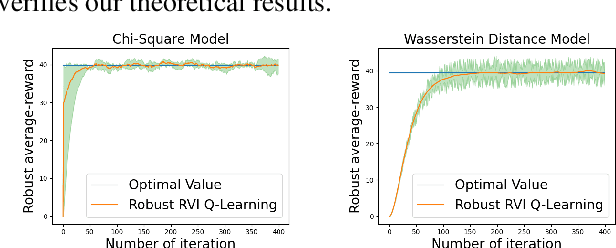
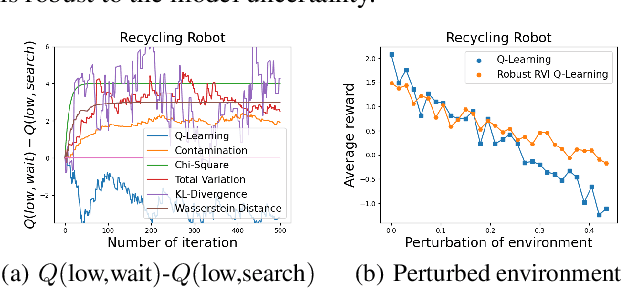
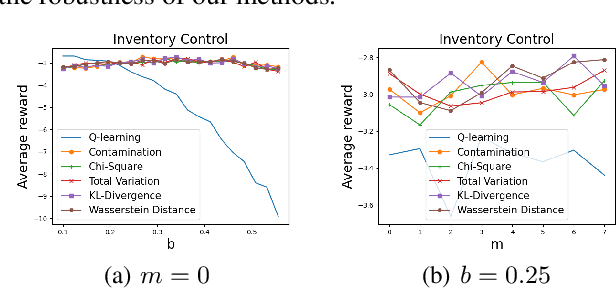
Robust Markov decision processes (MDPs) address the challenge of model uncertainty by optimizing the worst-case performance over an uncertainty set of MDPs. In this paper, we focus on the robust average-reward MDPs under the model-free setting. We first theoretically characterize the structure of solutions to the robust average-reward Bellman equation, which is essential for our later convergence analysis. We then design two model-free algorithms, robust relative value iteration (RVI) TD and robust RVI Q-learning, and theoretically prove their convergence to the optimal solution. We provide several widely used uncertainty sets as examples, including those defined by the contamination model, total variation, Chi-squared divergence, Kullback-Leibler (KL) divergence and Wasserstein distance.

On the Robustness of AlphaFold: A COVID-19 Case Study

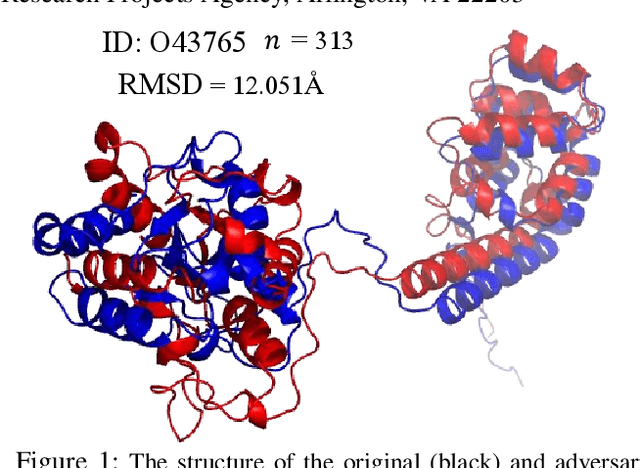
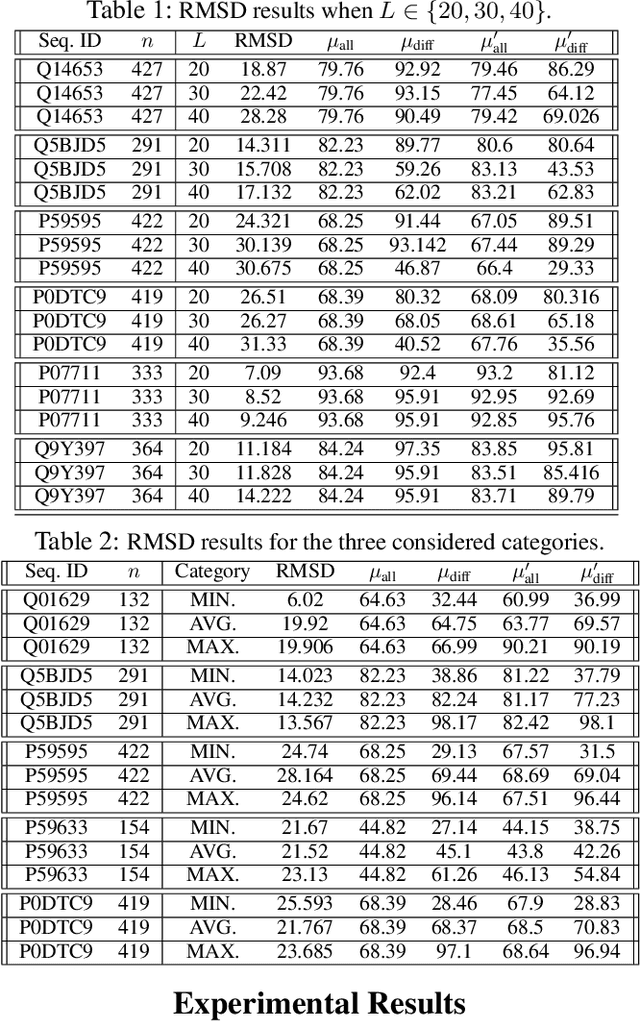
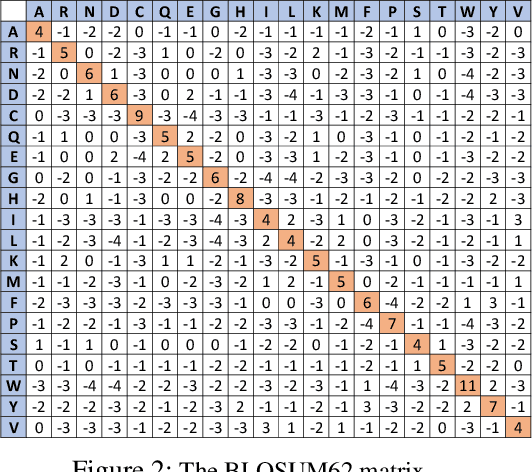
Protein folding neural networks (PFNNs) such as AlphaFold predict remarkably accurate structures of proteins compared to other approaches. However, the robustness of such networks has heretofore not been explored. This is particularly relevant given the broad social implications of such technologies and the fact that biologically small perturbations in the protein sequence do not generally lead to drastic changes in the protein structure. In this paper, we demonstrate that AlphaFold does not exhibit such robustness despite its high accuracy. This raises the challenge of detecting and quantifying the extent to which these predicted protein structures can be trusted. To measure the robustness of the predicted structures, we utilize (i) the root-mean-square deviation (RMSD) and (ii) the Global Distance Test (GDT) similarity measure between the predicted structure of the original sequence and the structure of its adversarially perturbed version. We prove that the problem of minimally perturbing protein sequences to fool protein folding neural networks is NP-complete. Based on the well-established BLOSUM62 sequence alignment scoring matrix, we generate adversarial protein sequences and show that the RMSD between the predicted protein structure and the structure of the original sequence are very large when the adversarial changes are bounded by (i) 20 units in the BLOSUM62 distance, and (ii) five residues (out of hundreds or thousands of residues) in the given protein sequence. In our experimental evaluation, we consider 111 COVID-19 proteins in the Universal Protein resource (UniProt), a central resource for protein data managed by the European Bioinformatics Institute, Swiss Institute of Bioinformatics, and the US Protein Information Resource. These result in an overall GDT similarity test score average of around 34%, demonstrating a substantial drop in the performance of AlphaFold.

Robust Average-Reward Markov Decision Processes

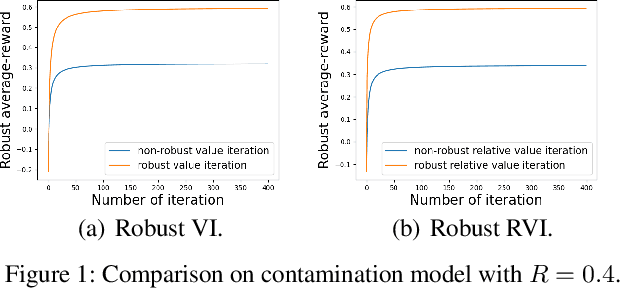
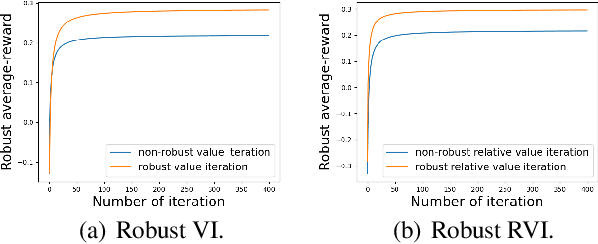
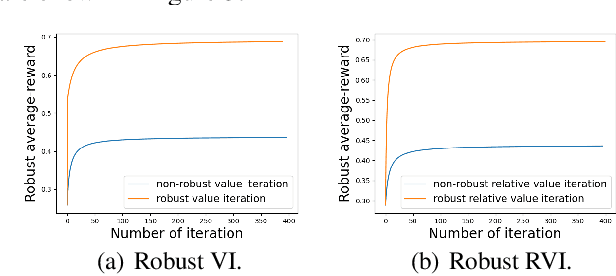
In robust Markov decision processes (MDPs), the uncertainty in the transition kernel is addressed by finding a policy that optimizes the worst-case performance over an uncertainty set of MDPs. While much of the literature has focused on discounted MDPs, robust average-reward MDPs remain largely unexplored. In this paper, we focus on robust average-reward MDPs, where the goal is to find a policy that optimizes the worst-case average reward over an uncertainty set. We first take an approach that approximates average-reward MDPs using discounted MDPs. We prove that the robust discounted value function converges to the robust average-reward as the discount factor $\gamma$ goes to $1$, and moreover, when $\gamma$ is large, any optimal policy of the robust discounted MDP is also an optimal policy of the robust average-reward. We further design a robust dynamic programming approach, and theoretically characterize its convergence to the optimum. Then, we investigate robust average-reward MDPs directly without using discounted MDPs as an intermediate step. We derive the robust Bellman equation for robust average-reward MDPs, prove that the optimal policy can be derived from its solution, and further design a robust relative value iteration algorithm that provably finds its solution, or equivalently, the optimal robust policy.

BOSS: Bidirectional One-Shot Synthesis of Adversarial Examples

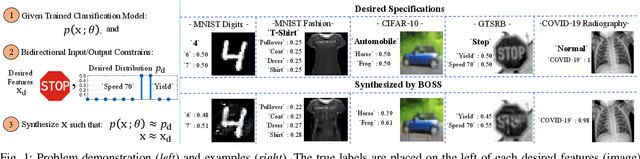
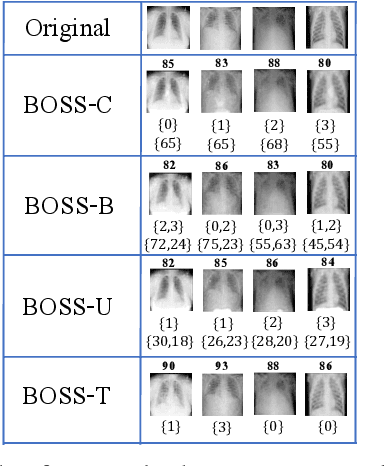
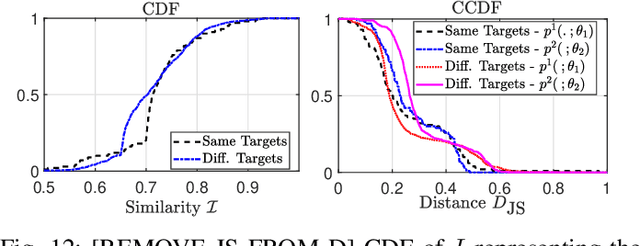
The design of additive imperceptible perturbations to the inputs of deep classifiers to maximize their misclassification rates is a central focus of adversarial machine learning. An alternative approach is to synthesize adversarial examples from scratch using GAN-like structures, albeit with the use of large amounts of training data. By contrast, this paper considers one-shot synthesis of adversarial examples; the inputs are synthesized from scratch to induce arbitrary soft predictions at the output of pre-trained models, while simultaneously maintaining high similarity to specified inputs. To this end, we present a problem that encodes objectives on the distance between the desired and output distributions of the trained model and the similarity between such inputs and the synthesized examples. We prove that the formulated problem is NP-complete. Then, we advance a generative approach to the solution in which the adversarial examples are obtained as the output of a generative network whose parameters are iteratively updated by optimizing surrogate loss functions for the dual-objective. We demonstrate the generality and versatility of the framework and approach proposed through applications to the design of targeted adversarial attacks, generation of decision boundary samples, and synthesis of low confidence classification inputs. The approach is further extended to an ensemble of models with different soft output specifications. The experimental results verify that the targeted and confidence reduction attack methods developed perform on par with state-of-the-art algorithms.

Learning Probabilistic Reward Machines from Non-Markovian Stochastic Reward Processes

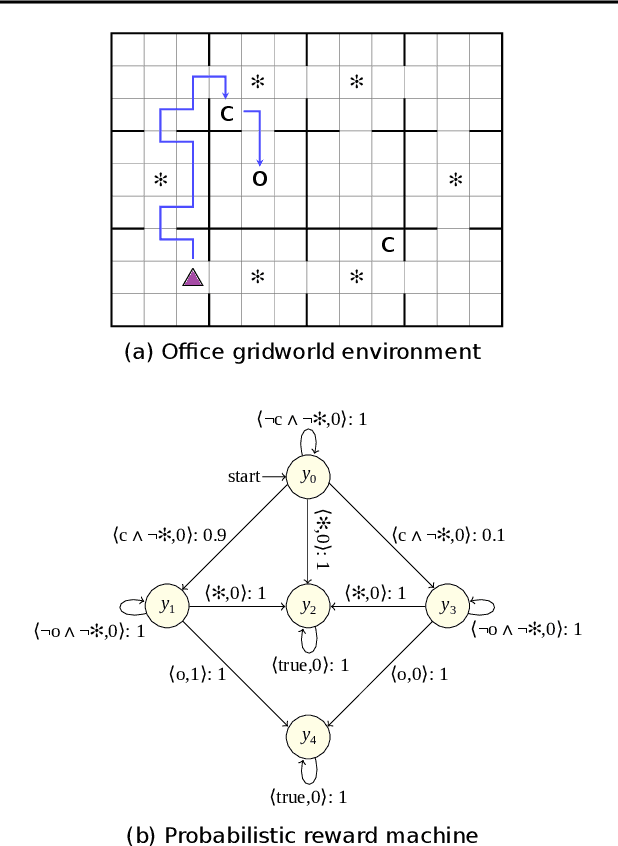
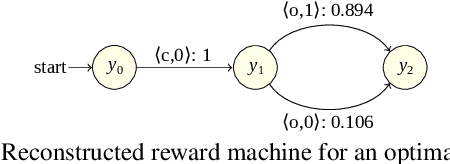
The success of reinforcement learning in typical settings is, in part, predicated on underlying Markovian assumptions on the reward signal by which an agent learns optimal policies. In recent years, the use of reward machines has relaxed this assumption by enabling a structured representation of non-Markovian rewards. In particular, such representations can be used to augment the state space of the underlying decision process, thereby facilitating non-Markovian reinforcement learning. However, these reward machines cannot capture the semantics of stochastic reward signals. In this paper, we make progress on this front by introducing probabilistic reward machines (PRMs) as a representation of non-Markovian stochastic rewards. We present an algorithm to learn PRMs from the underlying decision process as well as to learn the PRM representation of a given decision-making policy.

Controller Synthesis for Omega-Regular and Steady-State Specifications

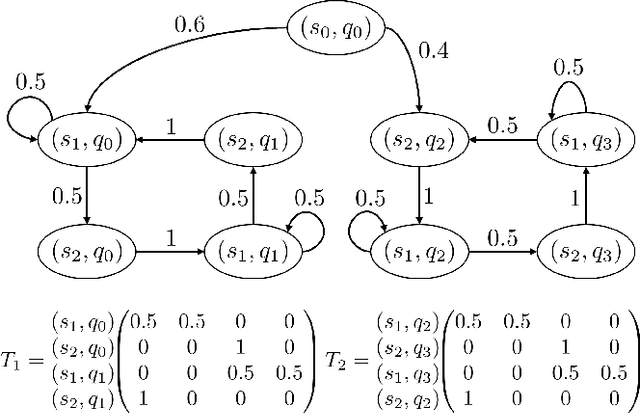
Given a Markov decision process (MDP) and a linear-time ($\omega$-regular or LTL) specification, the controller synthesis problem aims to compute the optimal policy that satisfies the specification. More recently, problems that reason over the asymptotic behavior of systems have been proposed through the lens of steady-state planning. This entails finding a control policy for an MDP such that the Markov chain induced by the solution policy satisfies a given set of constraints on its steady-state distribution. This paper studies a generalization of the controller synthesis problem for a linear-time specification under steady-state constraints on the asymptotic behavior. We present an algorithm to find a deterministic policy satisfying $\omega$-regular and steady-state constraints by characterizing the solutions as an integer linear program, and experimentally evaluate our approach.

A Multi-criteria Approach for Fast and Outlier-aware Representative Selection from Manifolds

The problem of representative selection amounts to sampling few informative exemplars from large datasets. This paper presents MOSAIC, a novel representative selection approach from high-dimensional data that may exhibit non-linear structures. Resting upon a novel quadratic formulation, Our method advances a multi-criteria selection approach that maximizes the global representation power of the sampled subset, ensures diversity, and rejects disruptive information by effectively detecting outliers. Through theoretical analyses we characterize the obtained sketch and reveal that the sampled representatives maximize a well-defined notion of data coverage in a transformed space. In addition, we present a highly scalable randomized implementation of the proposed algorithm shown to bring about substantial speedups. MOSAIC's superiority in achieving the desired characteristics of a representative subset all at once while exhibiting remarkable robustness to various outlier types is demonstrated via extensive experiments conducted on both real and synthetic data with comparisons to state-of-the-art algorithms.

Rediscovering Deep Neural Networks in Finite-State Distributions

We propose a new way of thinking about deep neural networks, in which the linear and non-linear components of the network are naturally derived and justified in terms of principles in probability theory. In particular, the models constructed in our framework assign probabilities to uncertain realizations, leading to Kullback-Leibler Divergence (KLD) as the linear layer. In our model construction, we also arrive at a structure similar to ReLU activation supported with Bayes' theorem. The non-linearities in our framework are normalization layers with ReLU and Sigmoid as element-wise approximations. Additionally, the pooling function is derived as a marginalization of spatial random variables according to the mechanics of the framework. As such, Max Pooling is an approximation to the aforementioned marginalization process. Since our models are comprised of finite state distributions (FSD) as variables and parameters, exact computation of information-theoretic quantities such as entropy and KLD is possible, thereby providing more objective measures to analyze networks. Unlike existing designs that rely on heuristics, the proposed framework restricts subjective interpretations of CNNs and sheds light on the functionality of neural networks from a completely new perspective.