Robust Average-Reward Markov Decision Processes
Paper and Code
Jan 02, 2023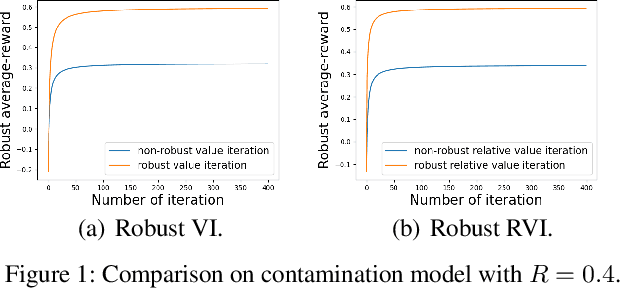
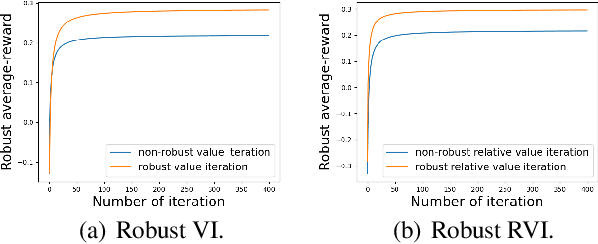
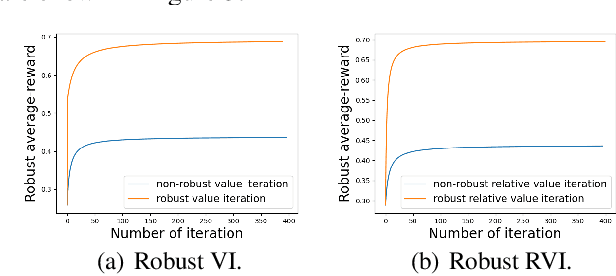
In robust Markov decision processes (MDPs), the uncertainty in the transition kernel is addressed by finding a policy that optimizes the worst-case performance over an uncertainty set of MDPs. While much of the literature has focused on discounted MDPs, robust average-reward MDPs remain largely unexplored. In this paper, we focus on robust average-reward MDPs, where the goal is to find a policy that optimizes the worst-case average reward over an uncertainty set. We first take an approach that approximates average-reward MDPs using discounted MDPs. We prove that the robust discounted value function converges to the robust average-reward as the discount factor $\gamma$ goes to $1$, and moreover, when $\gamma$ is large, any optimal policy of the robust discounted MDP is also an optimal policy of the robust average-reward. We further design a robust dynamic programming approach, and theoretically characterize its convergence to the optimum. Then, we investigate robust average-reward MDPs directly without using discounted MDPs as an intermediate step. We derive the robust Bellman equation for robust average-reward MDPs, prove that the optimal policy can be derived from its solution, and further design a robust relative value iteration algorithm that provably finds its solution, or equivalently, the optimal robust policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge