Mahlagha Sedghi
A Multi-criteria Approach for Fast and Outlier-aware Representative Selection from Manifolds
Mar 12, 2020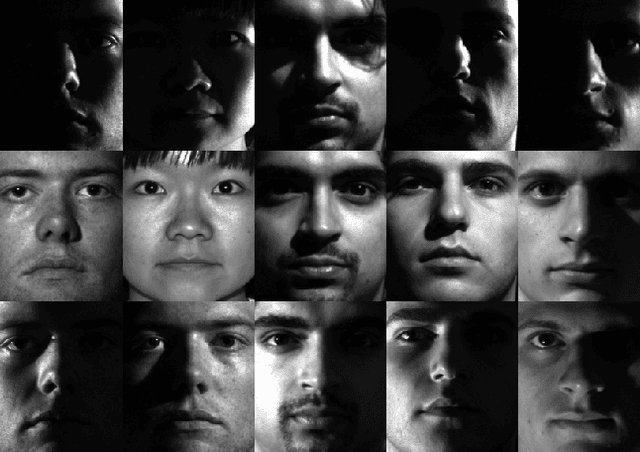


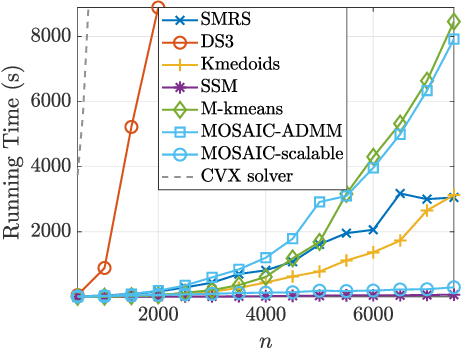
Abstract:The problem of representative selection amounts to sampling few informative exemplars from large datasets. This paper presents MOSAIC, a novel representative selection approach from high-dimensional data that may exhibit non-linear structures. Resting upon a novel quadratic formulation, Our method advances a multi-criteria selection approach that maximizes the global representation power of the sampled subset, ensures diversity, and rejects disruptive information by effectively detecting outliers. Through theoretical analyses we characterize the obtained sketch and reveal that the sampled representatives maximize a well-defined notion of data coverage in a transformed space. In addition, we present a highly scalable randomized implementation of the proposed algorithm shown to bring about substantial speedups. MOSAIC's superiority in achieving the desired characteristics of a representative subset all at once while exhibiting remarkable robustness to various outlier types is demonstrated via extensive experiments conducted on both real and synthetic data with comparisons to state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge