Understanding How Nonlinear Layers Create Linearly Separable Features for Low-Dimensional Data

Deep neural networks have attained remarkable success across diverse classification tasks. Recent empirical studies have shown that deep networks learn features that are linearly separable across classes. However, these findings often lack rigorous justifications, even under relatively simple settings. In this work, we address this gap by examining the linear separation capabilities of shallow nonlinear networks. Specifically, inspired by the low intrinsic dimensionality of image data, we model inputs as a union of low-dimensional subspaces (UoS) and demonstrate that a single nonlinear layer can transform such data into linearly separable sets. Theoretically, we show that this transformation occurs with high probability when using random weights and quadratic activations. Notably, we prove this can be achieved when the network width scales polynomially with the intrinsic dimension of the data rather than the ambient dimension. Experimental results corroborate these theoretical findings and demonstrate that similar linear separation properties hold in practical scenarios beyond our analytical scope. This work bridges the gap between empirical observations and theoretical understanding of the separation capacity of nonlinear networks, offering deeper insights into model interpretability and generalization.

Explaining and Mitigating the Modality Gap in Contrastive Multimodal Learning

Multimodal learning has recently gained significant popularity, demonstrating impressive performance across various zero-shot classification tasks and a range of perceptive and generative applications. Models such as Contrastive Language-Image Pretraining (CLIP) are designed to bridge different modalities, such as images and text, by learning a shared representation space through contrastive learning. Despite their success, the working mechanisms underlying multimodal learning are not yet well understood. Notably, these models often exhibit a modality gap, where different modalities occupy distinct regions within the shared representation space. In this work, we conduct an in-depth analysis of the emergence of modality gap by characterizing the gradient flow learning dynamics. Specifically, we identify the critical roles of mismatched data pairs and a learnable temperature parameter in causing and perpetuating the modality gap during training. Furthermore, our theoretical insights are validated through experiments on practical CLIP models. These findings provide principled guidance for mitigating the modality gap, including strategies such as appropriate temperature scheduling and modality swapping. Additionally, we demonstrate that closing the modality gap leads to improved performance on tasks such as image-text retrieval.

Compressible Dynamics in Deep Overparameterized Low-Rank Learning & Adaptation

While overparameterization in machine learning models offers great benefits in terms of optimization and generalization, it also leads to increased computational requirements as model sizes grow. In this work, we show that by leveraging the inherent low-dimensional structures of data and compressible dynamics within the model parameters, we can reap the benefits of overparameterization without the computational burdens. In practice, we demonstrate the effectiveness of this approach for deep low-rank matrix completion as well as fine-tuning language models. Our approach is grounded in theoretical findings for deep overparameterized low-rank matrix recovery, where we show that the learning dynamics of each weight matrix are confined to an invariant low-dimensional subspace. Consequently, we can construct and train compact, highly compressed factorizations possessing the same benefits as their overparameterized counterparts. In the context of deep matrix completion, our technique substantially improves training efficiency while retaining the advantages of overparameterization. For language model fine-tuning, we propose a method called "Deep LoRA", which improves the existing low-rank adaptation (LoRA) technique, leading to reduced overfitting and a simplified hyperparameter setup, while maintaining comparable efficiency. We validate the effectiveness of Deep LoRA on natural language tasks, particularly when fine-tuning with limited data.

Understanding Deep Representation Learning via Layerwise Feature Compression and Discrimination

Over the past decade, deep learning has proven to be a highly effective tool for learning meaningful features from raw data. However, it remains an open question how deep networks perform hierarchical feature learning across layers. In this work, we attempt to unveil this mystery by investigating the structures of intermediate features. Motivated by our empirical findings that linear layers mimic the roles of deep layers in nonlinear networks for feature learning, we explore how deep linear networks transform input data into output by investigating the output (i.e., features) of each layer after training in the context of multi-class classification problems. Toward this goal, we first define metrics to measure within-class compression and between-class discrimination of intermediate features, respectively. Through theoretical analysis of these two metrics, we show that the evolution of features follows a simple and quantitative pattern from shallow to deep layers when the input data is nearly orthogonal and the network weights are minimum-norm, balanced, and approximate low-rank: Each layer of the linear network progressively compresses within-class features at a geometric rate and discriminates between-class features at a linear rate with respect to the number of layers that data have passed through. To the best of our knowledge, this is the first quantitative characterization of feature evolution in hierarchical representations of deep linear networks. Empirically, our extensive experiments not only validate our theoretical results numerically but also reveal a similar pattern in deep nonlinear networks which aligns well with recent empirical studies. Moreover, we demonstrate the practical implications of our results in transfer learning. Our code is available at \url{https://github.com/Heimine/PNC_DLN}.

The Law of Parsimony in Gradient Descent for Learning Deep Linear Networks

Over the past few years, an extensively studied phenomenon in training deep networks is the implicit bias of gradient descent towards parsimonious solutions. In this work, we investigate this phenomenon by narrowing our focus to deep linear networks. Through our analysis, we reveal a surprising "law of parsimony" in the learning dynamics when the data possesses low-dimensional structures. Specifically, we show that the evolution of gradient descent starting from orthogonal initialization only affects a minimal portion of singular vector spaces across all weight matrices. In other words, the learning process happens only within a small invariant subspace of each weight matrix, despite the fact that all weight parameters are updated throughout training. This simplicity in learning dynamics could have significant implications for both efficient training and a better understanding of deep networks. First, the analysis enables us to considerably improve training efficiency by taking advantage of the low-dimensional structure in learning dynamics. We can construct smaller, equivalent deep linear networks without sacrificing the benefits associated with the wider counterparts. Second, it allows us to better understand deep representation learning by elucidating the linear progressive separation and concentration of representations from shallow to deep layers. We also conduct numerical experiments to support our theoretical results. The code for our experiments can be found at https://github.com/cjyaras/lawofparsimony.

Neural Collapse with Normalized Features: A Geometric Analysis over the Riemannian Manifold

When training overparameterized deep networks for classification tasks, it has been widely observed that the learned features exhibit a so-called "neural collapse" phenomenon. More specifically, for the output features of the penultimate layer, for each class the within-class features converge to their means, and the means of different classes exhibit a certain tight frame structure, which is also aligned with the last layer's classifier. As feature normalization in the last layer becomes a common practice in modern representation learning, in this work we theoretically justify the neural collapse phenomenon for normalized features. Based on an unconstrained feature model, we simplify the empirical loss function in a multi-class classification task into a nonconvex optimization problem over the Riemannian manifold by constraining all features and classifiers over the sphere. In this context, we analyze the nonconvex landscape of the Riemannian optimization problem over the product of spheres, showing a benign global landscape in the sense that the only global minimizers are the neural collapse solutions while all other critical points are strict saddles with negative curvature. Experimental results on practical deep networks corroborate our theory and demonstrate that better representations can be learned faster via feature normalization.

Randomized Histogram Matching: A Simple Augmentation for Unsupervised Domain Adaptation in Overhead Imagery

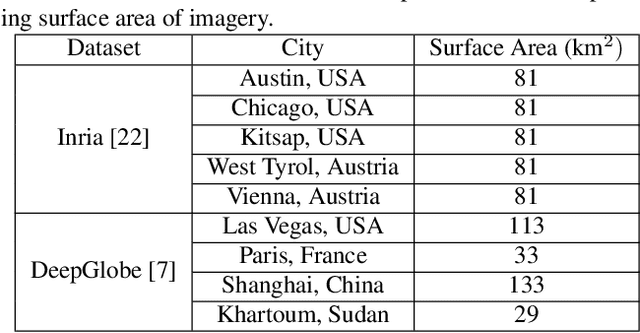
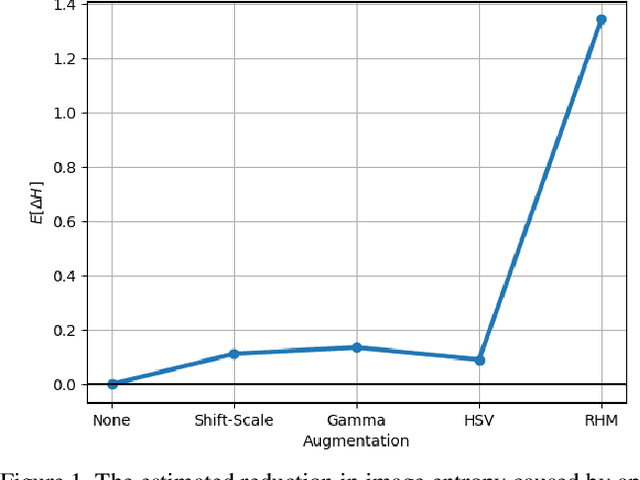
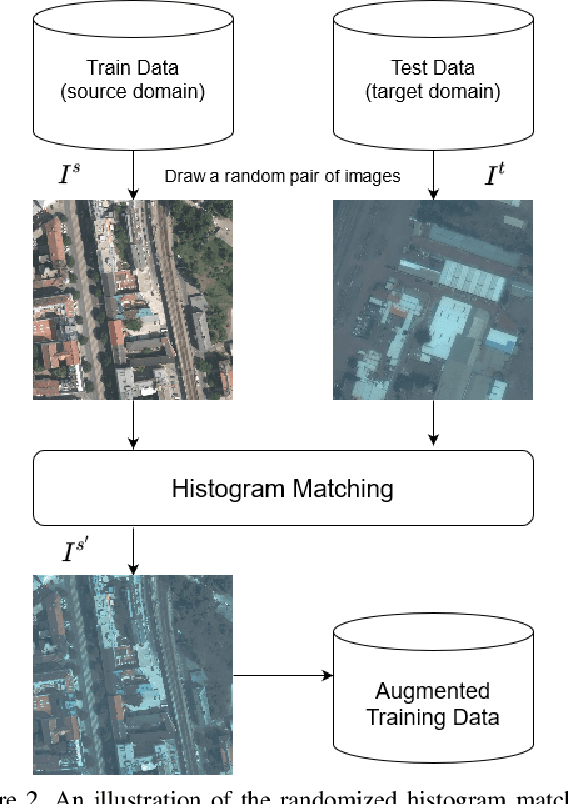
Modern deep neural networks (DNNs) achieve highly accurate results for many recognition tasks on overhead (e.g., satellite) imagery. One challenge however is visual domain shifts (i.e., statistical changes), which can cause the accuracy of DNNs to degrade substantially and unpredictably when tested on new sets of imagery. In this work we model domain shifts caused by variations in imaging hardware, lighting, and other conditions as non-linear pixel-wise transformations; and we show that modern DNNs can become largely invariant to these types of transformations, if provided with appropriate training data augmentation. In general, however, we do not know the transformation between two sets of imagery. To overcome this problem, we propose a simple real-time unsupervised training augmentation technique, termed randomized histogram matching (RHM). We conduct experiments with two large public benchmark datasets for building segmentation and find that RHM consistently yields comparable performance to recent state-of-the-art unsupervised domain adaptation approaches despite being simpler and faster. RHM also offers substantially better performance than other comparably simple approaches that are widely-used in overhead imagery.