Diffusion Posterior Sampling for General Noisy Inverse Problems

Diffusion models have been recently studied as powerful generative inverse problem solvers, owing to their high quality reconstructions and the ease of combining existing iterative solvers. However, most works focus on solving simple linear inverse problems in noiseless settings, which significantly under-represents the complexity of real-world problems. In this work, we extend diffusion solvers to efficiently handle general noisy (non)linear inverse problems via the Laplace approximation of the posterior sampling. Interestingly, the resulting posterior sampling scheme is a blended version of diffusion sampling with the manifold constrained gradient without a strict measurement consistency projection step, yielding a more desirable generative path in noisy settings compared to the previous studies. Our method demonstrates that diffusion models can incorporate various measurement noise statistics such as Gaussian and Poisson, and also efficiently handle noisy nonlinear inverse problems such as Fourier phase retrieval and non-uniform deblurring.

Bilevel learning of l1-regularizers with closed-form gradients(BLORC)

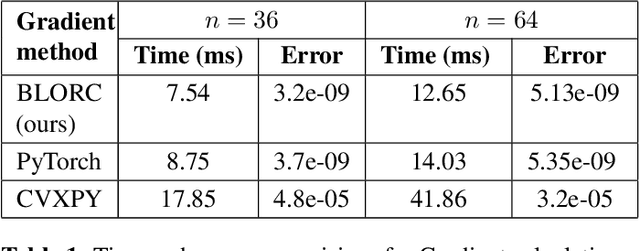
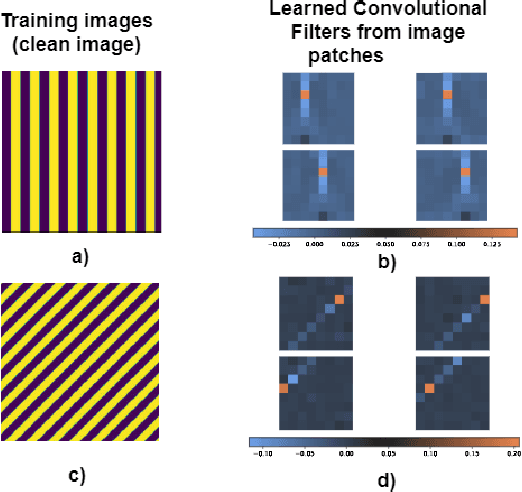
We present a method for supervised learning of sparsity-promoting regularizers, a key ingredient in many modern signal reconstruction problems. The parameters of the regularizer are learned to minimize the mean squared error of reconstruction on a training set of ground truth signal and measurement pairs. Training involves solving a challenging bilevel optimization problem with a nonsmooth lower-level objective. We derive an expression for the gradient of the training loss using the implicit closed-form solution of the lower-level variational problem given by its dual problem, and provide an accompanying gradient descent algorithm (dubbed BLORC) to minimize the loss. Our experiments on simple natural images and for denoising 1D signals show that the proposed method can learn meaningful operators and the analytical gradients calculated are faster than standard automatic differentiation methods. While the approach we present is applied to denoising, we believe that it can be adapted to a wide-variety of inverse problems with linear measurement models, thus giving it applicability in a wide range of scenarios.