Low-Bit Quantization of Bandlimited Graph Signals via Iterative Methods

We study the quantization of real-valued bandlimited signals on graphs, focusing on low-bit representations. We propose iterative noise-shaping algorithms for quantization, including sampling approaches with and without vertex replacement. The methods leverage the spectral properties of the graph Laplacian and exploit graph incoherence to achieve high-fidelity approximations. Theoretical guarantees are provided for the random sampling method, and extensive numerical experiments on synthetic and real-world graphs illustrate the efficiency and robustness of the proposed schemes.

Privacy-Preserving UCB Decision Process Verification via zk-SNARKs

With the increasingly widespread application of machine learning, how to strike a balance between protecting the privacy of data and algorithm parameters and ensuring the verifiability of machine learning has always been a challenge. This study explores the intersection of reinforcement learning and data privacy, specifically addressing the Multi-Armed Bandit (MAB) problem with the Upper Confidence Bound (UCB) algorithm. We introduce zkUCB, an innovative algorithm that employs the Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (zk-SNARKs) to enhance UCB. zkUCB is carefully designed to safeguard the confidentiality of training data and algorithmic parameters, ensuring transparent UCB decision-making. Experiments highlight zkUCB's superior performance, attributing its enhanced reward to judicious quantization bit usage that reduces information entropy in the decision-making process. zkUCB's proof size and verification time scale linearly with the execution steps of zkUCB. This showcases zkUCB's adept balance between data security and operational efficiency. This approach contributes significantly to the ongoing discourse on reinforcing data privacy in complex decision-making processes, offering a promising solution for privacy-sensitive applications.

Implicit regularization in Heavy-ball momentum accelerated stochastic gradient descent

It is well known that the finite step-size ($h$) in Gradient Descent (GD) implicitly regularizes solutions to flatter minima. A natural question to ask is "Does the momentum parameter $\beta$ play a role in implicit regularization in Heavy-ball (H.B) momentum accelerated gradient descent (GD+M)?". To answer this question, first, we show that the discrete H.B momentum update (GD+M) follows a continuous trajectory induced by a modified loss, which consists of an original loss and an implicit regularizer. Then, we show that this implicit regularizer for (GD+M) is stronger than that of (GD) by factor of $(\frac{1+\beta}{1-\beta})$, thus explaining why (GD+M) shows better generalization performance and higher test accuracy than (GD). Furthermore, we extend our analysis to the stochastic version of gradient descent with momentum (SGD+M) and characterize the continuous trajectory of the update of (SGD+M) in a pointwise sense. We explore the implicit regularization in (SGD+M) and (GD+M) through a series of experiments validating our theory.

Manifold Denoising by Nonlinear Robust Principal Component Analysis

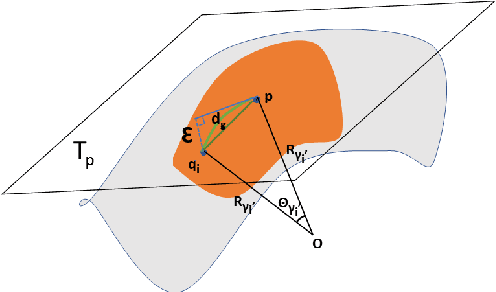
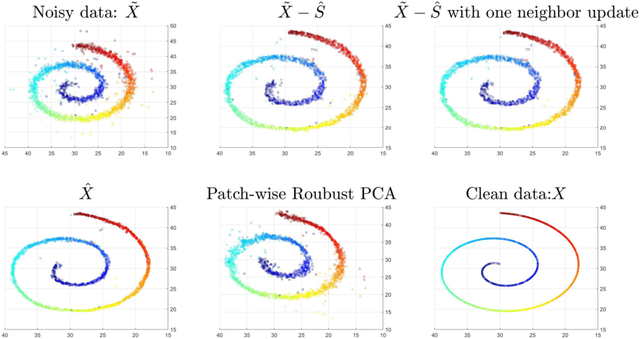
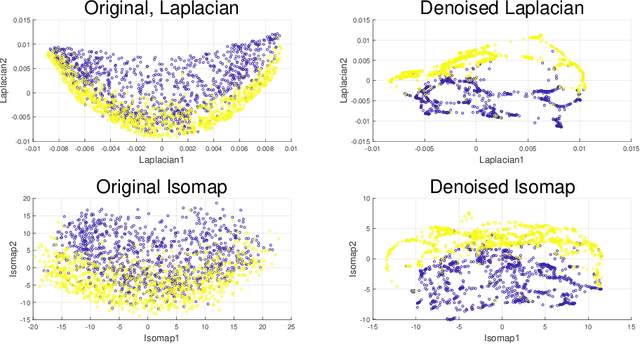
This paper extends robust principal component analysis (RPCA) to nonlinear manifolds. Suppose that the observed data matrix is the sum of a sparse component and a component drawn from some low dimensional manifold. Is it possible to separate them by using similar ideas as RPCA? Is there any benefit in treating the manifold as a whole as opposed to treating each local region independently? We answer these two questions affirmatively by proposing and analyzing an optimization framework that separates the sparse component from the manifold under noisy data. Theoretical error bounds are provided when the tangent spaces of the manifold satisfy certain incoherence conditions. We also provide a near optimal choice of the tuning parameters for the proposed optimization formulation with the help of a new curvature estimation method. The efficacy of our method is demonstrated on both synthetic and real datasets.