Shuyang Qin
Manifold Denoising by Nonlinear Robust Principal Component Analysis
Nov 10, 2019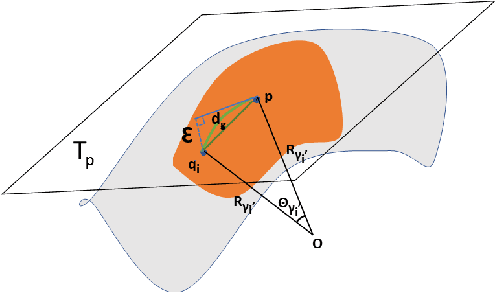
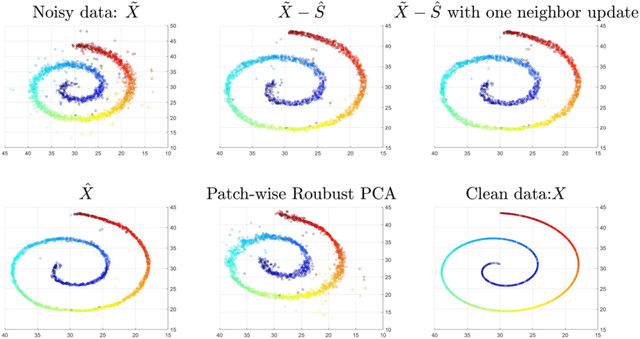
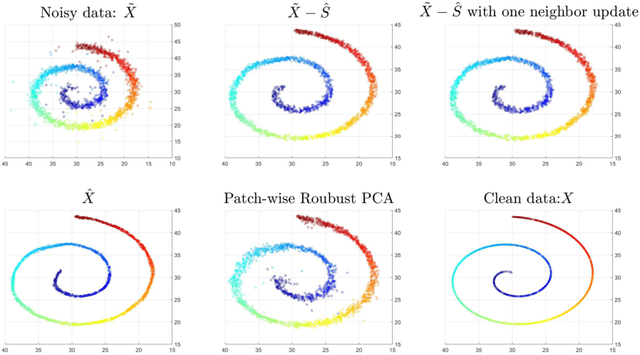
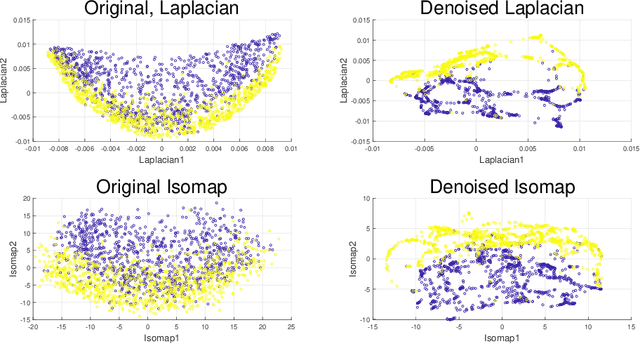
Abstract:This paper extends robust principal component analysis (RPCA) to nonlinear manifolds. Suppose that the observed data matrix is the sum of a sparse component and a component drawn from some low dimensional manifold. Is it possible to separate them by using similar ideas as RPCA? Is there any benefit in treating the manifold as a whole as opposed to treating each local region independently? We answer these two questions affirmatively by proposing and analyzing an optimization framework that separates the sparse component from the manifold under noisy data. Theoretical error bounds are provided when the tangent spaces of the manifold satisfy certain incoherence conditions. We also provide a near optimal choice of the tuning parameters for the proposed optimization formulation with the help of a new curvature estimation method. The efficacy of our method is demonstrated on both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge