Ningyu Sha
Fast algorithms for robust principal component analysis with an upper bound on the rank
Sep 03, 2020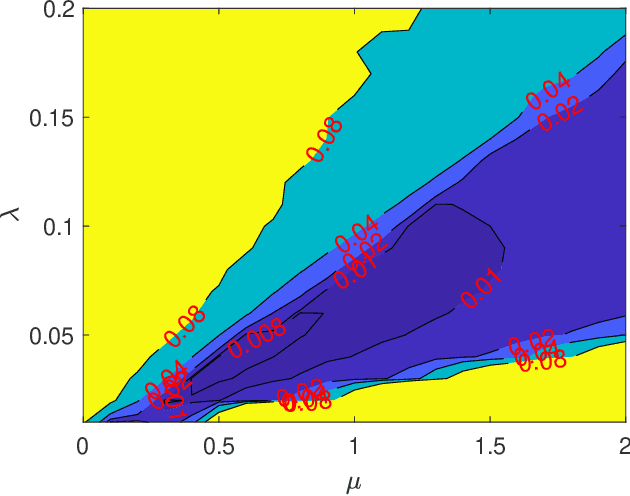
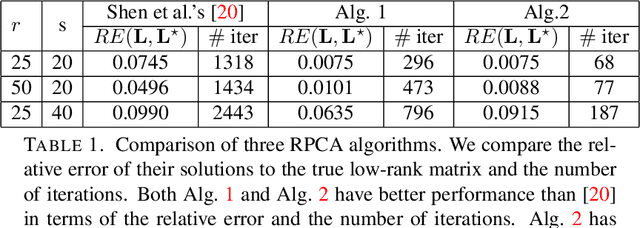
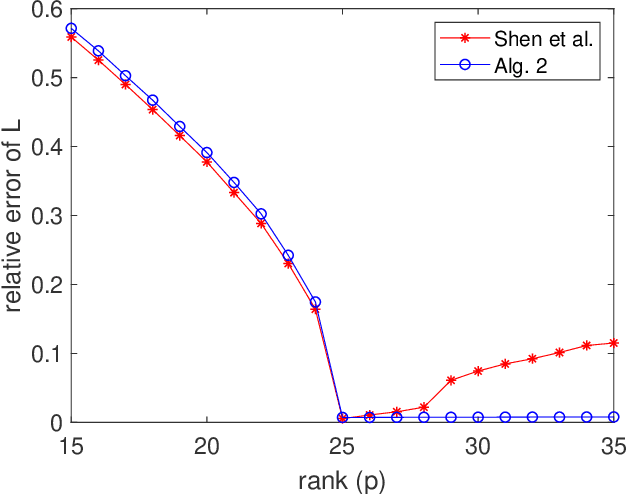
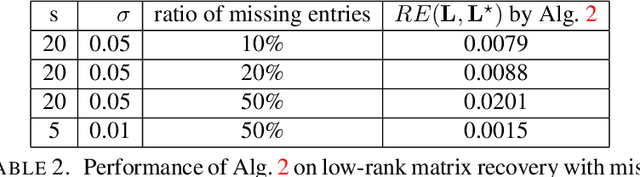
Abstract:The robust principal component analysis (RPCA) decomposes a data matrix into a low-rank part and a sparse part. There are mainly two types of algorithms for RPCA. The first type of algorithm applies regularization terms on the singular values of a matrix to obtain a low-rank matrix. However, calculating singular values can be very expensive for large matrices. The second type of algorithm replaces the low-rank matrix as the multiplication of two small matrices. They are faster than the first type because no singular value decomposition (SVD) is required. However, the rank of the low-rank matrix is required, and an accurate rank estimation is needed to obtain a reasonable solution. In this paper, we propose algorithms that combine both types. Our proposed algorithms require an upper bound of the rank and SVD on small matrices. First, they are faster than the first type because the cost of SVD on small matrices is negligible. Second, they are more robust than the second type because an upper bound of the rank instead of the exact rank is required. Furthermore, we apply the Gauss-Newton method to increase the speed of our algorithms. Numerical experiments show the better performance of our proposed algorithms.
Manifold Denoising by Nonlinear Robust Principal Component Analysis
Nov 10, 2019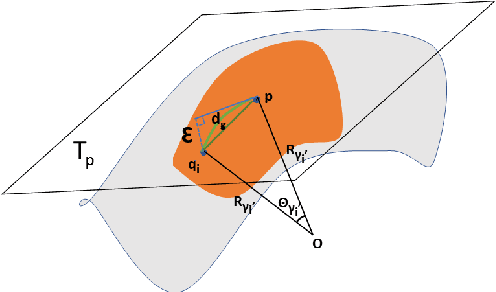
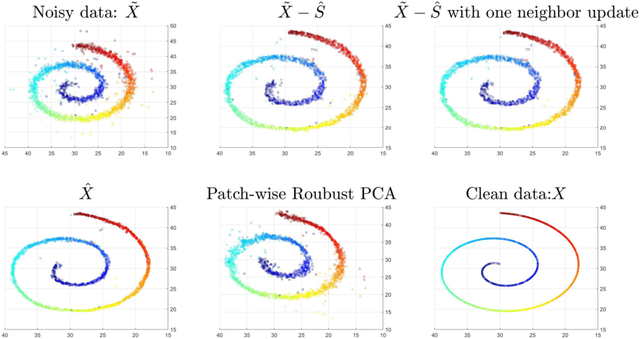
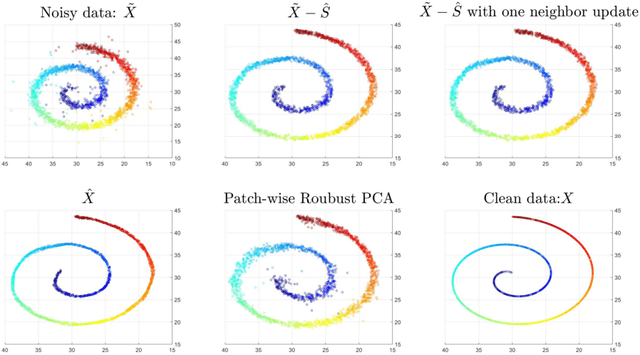
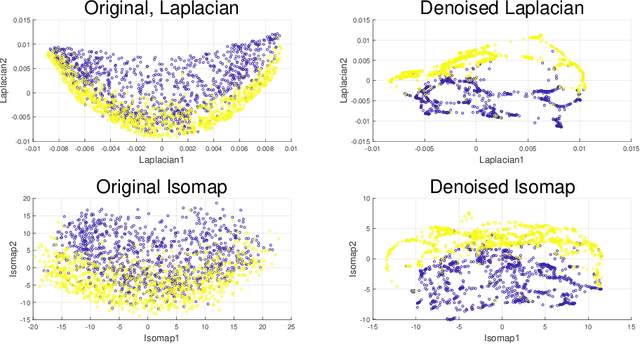
Abstract:This paper extends robust principal component analysis (RPCA) to nonlinear manifolds. Suppose that the observed data matrix is the sum of a sparse component and a component drawn from some low dimensional manifold. Is it possible to separate them by using similar ideas as RPCA? Is there any benefit in treating the manifold as a whole as opposed to treating each local region independently? We answer these two questions affirmatively by proposing and analyzing an optimization framework that separates the sparse component from the manifold under noisy data. Theoretical error bounds are provided when the tangent spaces of the manifold satisfy certain incoherence conditions. We also provide a near optimal choice of the tuning parameters for the proposed optimization formulation with the help of a new curvature estimation method. The efficacy of our method is demonstrated on both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge