A novel algorithm for the decomposition of non-stationary multidimensional and multivariate signals

The decomposition of a signal is a fundamental tool in many fields of research, including signal processing, geophysics, astrophysics, engineering, medicine, and many more. By breaking down complex signals into simpler oscillatory components we can enhance the understanding and processing of the data, unveiling hidden information contained in them. Traditional methods, such as Fourier analysis and wavelet transforms, which are effective in handling mono-dimensional stationary signals struggle with non-stationary data sets and they require, this is the case of the wavelet, the selection of predefined basis functions. In contrast, the Empirical Mode Decomposition (EMD) method and its variants, such as Iterative Filtering (IF), have emerged as effective nonlinear approaches, adapting to signals without any need for a priori assumptions. To accelerate these methods, the Fast Iterative Filtering (FIF) algorithm was developed, and further extensions, such as Multivariate FIF (MvFIF) and Multidimensional FIF (FIF2), have been proposed to handle higher-dimensional data. In this work, we introduce the Multidimensional and Multivariate Fast Iterative Filtering (MdMvFIF) technique, an innovative method that extends FIF to handle data that vary simultaneously in space and time. This new algorithm is capable of extracting Intrinsic Mode Functions (IMFs) from complex signals that vary in both space and time, overcoming limitations found in prior methods. The potentiality of the proposed method is demonstrated through applications to artificial and real-life signals, highlighting its versatility and effectiveness in decomposing multidimensional and multivariate nonstationary signals. The MdMvFIF method offers a powerful tool for advanced signal analysis across many scientific and engineering disciplines.

Structured and Balanced Multi-component and Multi-layer Neural Networks

In this work, we propose a balanced multi-component and multi-layer neural network (MMNN) structure to approximate functions with complex features with both accuracy and efficiency in terms of degrees of freedom and computation cost. The main idea is motivated by a multi-component, each of which can be approximated effectively by a single-layer network, and multi-layer decomposition in a "divide-and-conquer" type of strategy to deal with a complex function. While an easy modification to fully connected neural networks (FCNNs) or multi-layer perceptrons (MLPs) through the introduction of balanced multi-component structures in the network, MMNNs achieve a significant reduction of training parameters, a much more efficient training process, and a much improved accuracy compared to FCNNs or MLPs. Extensive numerical experiments are presented to illustrate the effectiveness of MMNNs in approximating high oscillatory functions and its automatic adaptivity in capturing localized features.

RRCNN$^{+}$: An Enhanced Residual Recursive Convolutional Neural Network for Non-stationary Signal Decomposition

Time-frequency analysis is an important and challenging task in many applications. Fourier and wavelet analysis are two classic methods that have achieved remarkable success in many fields. They also exhibit limitations when applied to nonlinear and non-stationary signals. To address this challenge, a series of nonlinear and adaptive methods, pioneered by the empirical mode decomposition method have been proposed. Their aim is to decompose a non-stationary signal into quasi-stationary components which reveal better features in the time-frequency analysis. Recently, inspired by deep learning, we proposed a novel method called residual recursive convolutional neural network (RRCNN). Not only RRCNN can achieve more stable decomposition than existing methods while batch processing large-scale signals with low computational cost, but also deep learning provides a unique perspective for non-stationary signal decomposition. In this study, we aim to further improve RRCNN with the help of several nimble techniques from deep learning and optimization to ameliorate the method and overcome some of the limitations of this technique.

RRCNN: A novel signal decomposition approach based on recurrent residue convolutional neural network

The decomposition of non-stationary signals is an important and challenging task in the field of signal time-frequency analysis. In the recent two decades, many signal decomposition methods led by the empirical mode decomposition, which was pioneered by Huang et al. in 1998, have been proposed by different research groups. However, they still have some limitations. For example, they are generally prone to boundary and mode mixing effects and are not very robust to noise. Inspired by the successful applications of deep learning in fields like image processing and natural language processing, and given the lack in the literature of works in which deep learning techniques are used directly to decompose non-stationary signals into simple oscillatory components, we use the convolutional neural network, residual structure and nonlinear activation function to compute in an innovative way the local average of the signal, and study a new non-stationary signal decomposition method under the framework of deep learning. We discuss the training process of the proposed model and study the convergence analysis of the learning algorithm. In the experiments, we evaluate the performance of the proposed model from two points of view: the calculation of the local average and the signal decomposition. Furthermore, we study the mode mixing, noise interference, and orthogonality properties of the decomposed components produced by the proposed method. All results show that the proposed model allows for better handling boundary effect, mode mixing effect, robustness, and the orthogonality of the decomposed components than existing methods.

Why Shallow Networks Struggle with Approximating and Learning High Frequency: A Numerical Study

In this work, a comprehensive numerical study involving analysis and experiments shows why a two-layer neural network has difficulties handling high frequencies in approximation and learning when machine precision and computation cost are important factors in real practice. In particular, the following fundamental computational issues are investigated: (1) the best accuracy one can achieve given a finite machine precision, (2) the computation cost to achieve a given accuracy, and (3) stability with respect to perturbations. The key to the study is the spectral analysis of the corresponding Gram matrix of the activation functions which also shows how the properties of the activation function play a role in the picture.

Neural Control of Parametric Solutions for High-dimensional Evolution PDEs

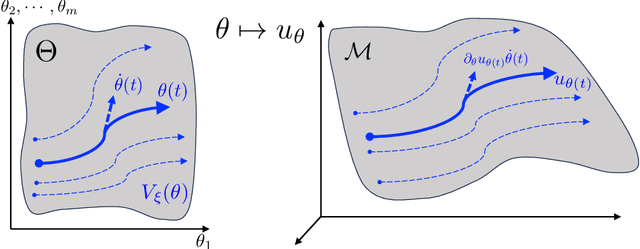
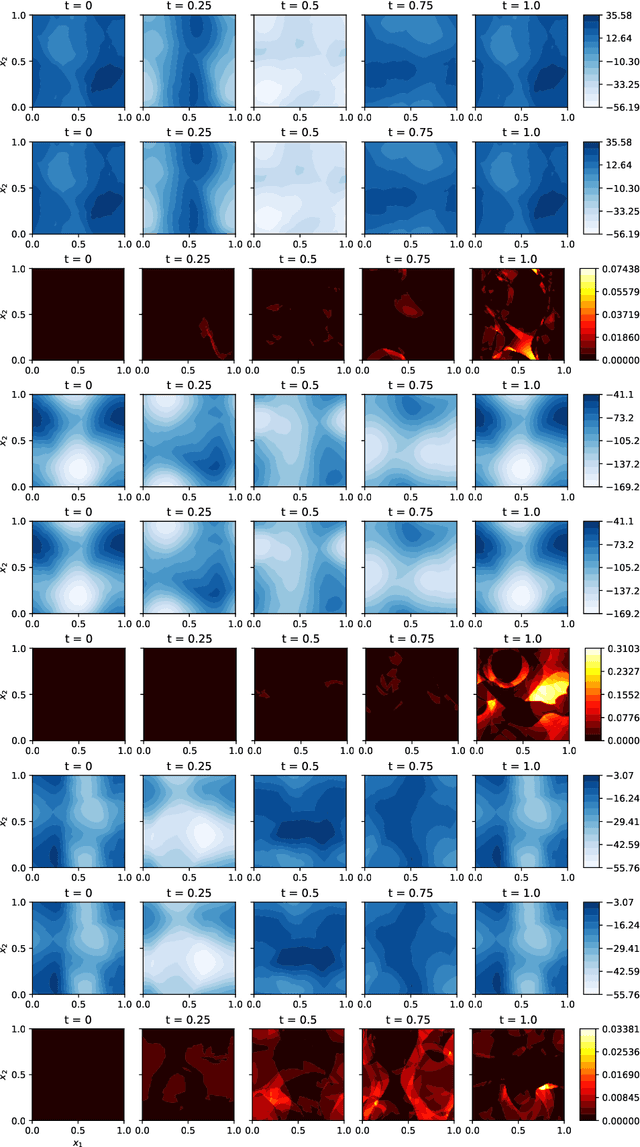
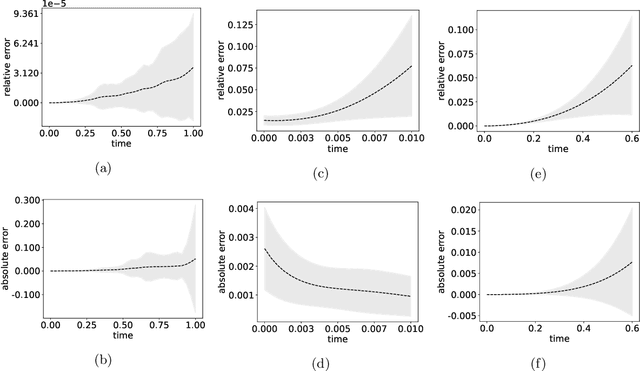
We develop a novel computational framework to approximate solution operators of evolution partial differential equations (PDEs). By employing a general nonlinear reduced-order model, such as a deep neural network, to approximate the solution of a given PDE, we realize that the evolution of the model parameter is a control problem in the parameter space. Based on this observation, we propose to approximate the solution operator of the PDE by learning the control vector field in the parameter space. From any initial value, this control field can steer the parameter to generate a trajectory such that the corresponding reduced-order model solves the PDE. This allows for substantially reduced computational cost to solve the evolution PDE with arbitrary initial conditions. We also develop comprehensive error analysis for the proposed method when solving a large class of semilinear parabolic PDEs. Numerical experiments on different high-dimensional evolution PDEs with various initial conditions demonstrate the promising results of the proposed method.

Discrete Langevin Sampler via Wasserstein Gradient Flow

Recently, a family of locally balanced (LB) samplers has demonstrated excellent performance at sampling and learning energy-based models (EBMs) in discrete spaces. However, the theoretical understanding of this success is limited. In this work, we show how LB functions give rise to LB dynamics corresponding to Wasserstein gradient flow in a discrete space. From first principles, previous LB samplers can then be seen as discretizations of the LB dynamics with respect to Hamming distance. Based on this observation, we propose a new algorithm, the Locally Balanced Jump (LBJ), by discretizing the LB dynamics with respect to simulation time. As a result, LBJ has a location-dependent "velocity" that allows it to make proposals with larger distances. Additionally, LBJ decouples each dimension into independent sub-processes, enabling convenient parallel implementation. We demonstrate the advantages of LBJ for sampling and learning in various binary and categorical distributions.

Scalable Computation of Monge Maps with General Costs

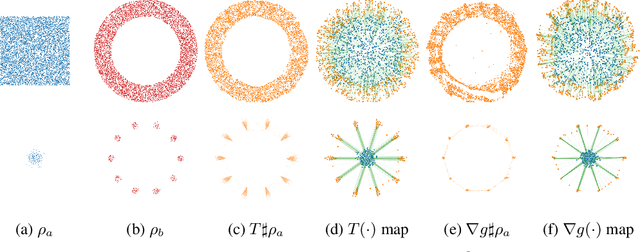
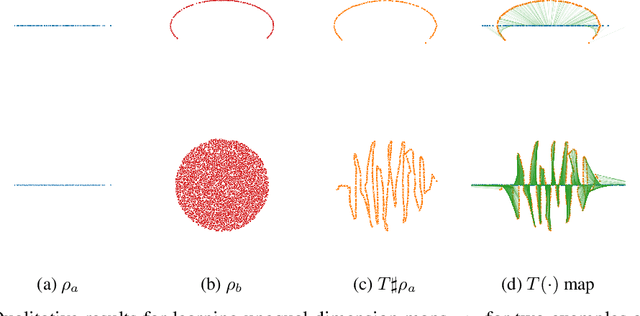
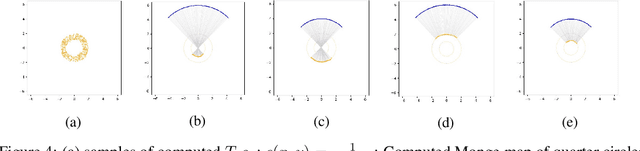
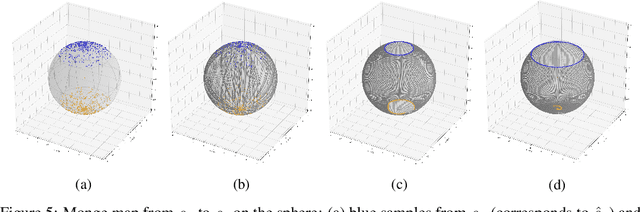
Monge map refers to the optimal transport map between two probability distributions and provides a principled approach to transform one distribution to another. In spite of the rapid developments of the numerical methods for optimal transport problems, computing the Monge maps remains challenging, especially for high dimensional problems. In this paper, we present a scalable algorithm for computing the Monge map between two probability distributions. Our algorithm is based on a weak form of the optimal transport problem, thus it only requires samples from the marginals instead of their analytic expressions, and can accommodate optimal transport between two distributions with different dimensions. Our algorithm is suitable for general cost functions, compared with other existing methods for estimating Monge maps using samples, which are usually for quadratic costs. The performance of our algorithms is demonstrated through a series of experiments with both synthetic and realistic data.

Mean Field Game GAN

We propose a novel mean field games (MFGs) based GAN(generative adversarial network) framework. To be specific, we utilize the Hopf formula in density space to rewrite MFGs as a primal-dual problem so that we are able to train the model via neural networks and samples. Our model is flexible due to the freedom of choosing various functionals within the Hopf formula. Moreover, our formulation mathematically avoids Lipschitz-1 constraint. The correctness and efficiency of our method are validated through several experiments.

Learning High Dimensional Wasserstein Geodesics

We propose a new formulation and learning strategy for computing the Wasserstein geodesic between two probability distributions in high dimensions. By applying the method of Lagrange multipliers to the dynamic formulation of the optimal transport (OT) problem, we derive a minimax problem whose saddle point is the Wasserstein geodesic. We then parametrize the functions by deep neural networks and design a sample based bidirectional learning algorithm for training. The trained networks enable sampling from the Wasserstein geodesic. As by-products, the algorithm also computes the Wasserstein distance and OT map between the marginal distributions. We demonstrate the performance of our algorithms through a series of experiments with both synthetic and realistic data.