Cosmos World Foundation Model Platform for Physical AI

Physical AI needs to be trained digitally first. It needs a digital twin of itself, the policy model, and a digital twin of the world, the world model. In this paper, we present the Cosmos World Foundation Model Platform to help developers build customized world models for their Physical AI setups. We position a world foundation model as a general-purpose world model that can be fine-tuned into customized world models for downstream applications. Our platform covers a video curation pipeline, pre-trained world foundation models, examples of post-training of pre-trained world foundation models, and video tokenizers. To help Physical AI builders solve the most critical problems of our society, we make our platform open-source and our models open-weight with permissive licenses available via https://github.com/NVIDIA/Cosmos.

Edify Image: High-Quality Image Generation with Pixel Space Laplacian Diffusion Models

We introduce Edify Image, a family of diffusion models capable of generating photorealistic image content with pixel-perfect accuracy. Edify Image utilizes cascaded pixel-space diffusion models trained using a novel Laplacian diffusion process, in which image signals at different frequency bands are attenuated at varying rates. Edify Image supports a wide range of applications, including text-to-image synthesis, 4K upsampling, ControlNets, 360 HDR panorama generation, and finetuning for image customization.

One-Step Diffusion Policy: Fast Visuomotor Policies via Diffusion Distillation

Diffusion models, praised for their success in generative tasks, are increasingly being applied to robotics, demonstrating exceptional performance in behavior cloning. However, their slow generation process stemming from iterative denoising steps poses a challenge for real-time applications in resource-constrained robotics setups and dynamically changing environments. In this paper, we introduce the One-Step Diffusion Policy (OneDP), a novel approach that distills knowledge from pre-trained diffusion policies into a single-step action generator, significantly accelerating response times for robotic control tasks. We ensure the distilled generator closely aligns with the original policy distribution by minimizing the Kullback-Leibler (KL) divergence along the diffusion chain, requiring only $2\%$-$10\%$ additional pre-training cost for convergence. We evaluated OneDP on 6 challenging simulation tasks as well as 4 self-designed real-world tasks using the Franka robot. The results demonstrate that OneDP not only achieves state-of-the-art success rates but also delivers an order-of-magnitude improvement in inference speed, boosting action prediction frequency from 1.5 Hz to 62 Hz, establishing its potential for dynamic and computationally constrained robotic applications. We share the project page at https://research.nvidia.com/labs/dir/onedp/.

A Chinese Continuous Sign Language Dataset Based on Complex Environments

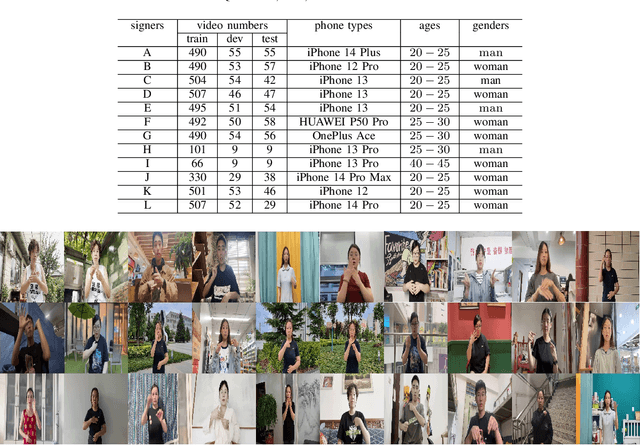
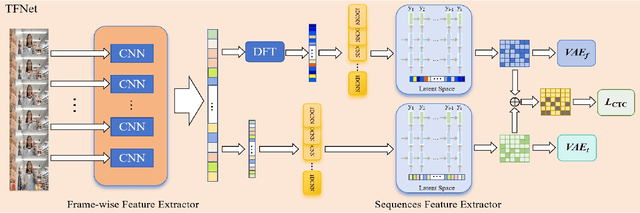
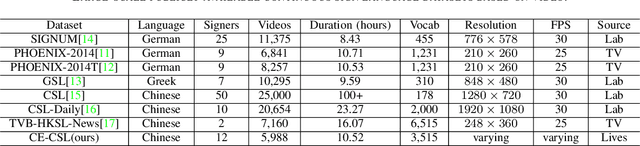
The current bottleneck in continuous sign language recognition (CSLR) research lies in the fact that most publicly available datasets are limited to laboratory environments or television program recordings, resulting in a single background environment with uniform lighting, which significantly deviates from the diversity and complexity found in real-life scenarios. To address this challenge, we have constructed a new, large-scale dataset for Chinese continuous sign language (CSL) based on complex environments, termed the complex environment - chinese sign language dataset (CE-CSL). This dataset encompasses 5,988 continuous CSL video clips collected from daily life scenes, featuring more than 70 different complex backgrounds to ensure representativeness and generalization capability. To tackle the impact of complex backgrounds on CSLR performance, we propose a time-frequency network (TFNet) model for continuous sign language recognition. This model extracts frame-level features and then utilizes both temporal and spectral information to separately derive sequence features before fusion, aiming to achieve efficient and accurate CSLR. Experimental results demonstrate that our approach achieves significant performance improvements on the CE-CSL, validating its effectiveness under complex background conditions. Additionally, our proposed method has also yielded highly competitive results when applied to three publicly available CSL datasets.

RefDrop: Controllable Consistency in Image or Video Generation via Reference Feature Guidance

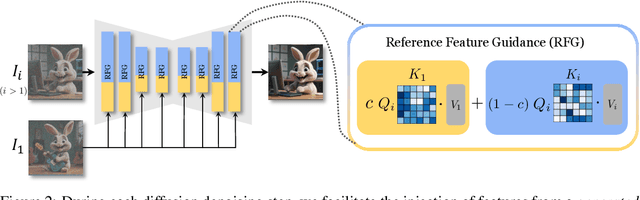
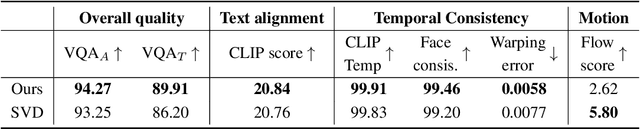
There is a rapidly growing interest in controlling consistency across multiple generated images using diffusion models. Among various methods, recent works have found that simply manipulating attention modules by concatenating features from multiple reference images provides an efficient approach to enhancing consistency without fine-tuning. Despite its popularity and success, few studies have elucidated the underlying mechanisms that contribute to its effectiveness. In this work, we reveal that the popular approach is a linear interpolation of image self-attention and cross-attention between synthesized content and reference features, with a constant rank-1 coefficient. Motivated by this observation, we find that a rank-1 coefficient is not necessary and simplifies the controllable generation mechanism. The resulting algorithm, which we coin as RefDrop, allows users to control the influence of reference context in a direct and precise manner. Besides further enhancing consistency in single-subject image generation, our method also enables more interesting applications, such as the consistent generation of multiple subjects, suppressing specific features to encourage more diverse content, and high-quality personalized video generation by boosting temporal consistency. Even compared with state-of-the-art image-prompt-based generators, such as IP-Adapter, RefDrop is competitive in terms of controllability and quality while avoiding the need to train a separate image encoder for feature injection from reference images, making it a versatile plug-and-play solution for any image or video diffusion model.

Generating Synthetic Datasets by Interpolating along Generalized Geodesics

Data for pretraining machine learning models often consists of collections of heterogeneous datasets. Although training on their union is reasonable in agnostic settings, it might be suboptimal when the target domain -- where the model will ultimately be used -- is known in advance. In that case, one would ideally pretrain only on the dataset(s) most similar to the target one. Instead of limiting this choice to those datasets already present in the pretraining collection, here we explore extending this search to all datasets that can be synthesized as `combinations' of them. We define such combinations as multi-dataset interpolations, formalized through the notion of generalized geodesics from optimal transport (OT) theory. We compute these geodesics using a recent notion of distance between labeled datasets, and derive alternative interpolation schemes based on it: using either barycentric projections or optimal transport maps, the latter computed using recent neural OT methods. These methods are scalable, efficient, and -- notably -- can be used to interpolate even between datasets with distinct and unrelated label sets. Through various experiments in transfer learning in computer vision, we demonstrate this is a promising new approach for targeted on-demand dataset synthesis.

Improved dimension dependence of a proximal algorithm for sampling

We propose a sampling algorithm that achieves superior complexity bounds in all the classical settings (strongly log-concave, log-concave, Logarithmic-Sobolev inequality (LSI), Poincar\'e inequality) as well as more general settings with semi-smooth or composite potentials. Our algorithm is based on the proximal sampler introduced in~\citet{lee2021structured}. The performance of this proximal sampler is determined by that of the restricted Gaussian oracle (RGO), a key step in the proximal sampler. The main contribution of this work is an inexact realization of RGO based on approximate rejection sampling. To bound the inexactness of RGO, we establish a new concentration inequality for semi-smooth functions over Gaussian distributions, extending the well-known concentration inequality for Lipschitz functions. Applying our RGO implementation to the proximal sampler, we achieve state-of-the-art complexity bounds in almost all settings. For instance, for strongly log-concave distributions, our method has complexity bound $\tilde\mathcal{O}(\kappa d^{1/2})$ without warm start, better than the minimax bound for MALA. For distributions satisfying the LSI, our bound is $\tilde \mathcal{O}(\hat \kappa d^{1/2})$ where $\hat \kappa$ is the ratio between smoothness and the LSI constant, better than all existing bounds.

Variational Wasserstein gradient flow

The gradient flow of a function over the space of probability densities with respect to the Wasserstein metric often exhibits nice properties and has been utilized in several machine learning applications. The standard approach to compute the Wasserstein gradient flow is the finite difference which discretizes the underlying space over a grid, and is not scalable. In this work, we propose a scalable proximal gradient type algorithm for Wasserstein gradient flow. The key of our method is a variational formulation of the objective function, which makes it possible to realize the JKO proximal map through a primal-dual optimization. This primal-dual problem can be efficiently solved by alternatively updating the parameters in the inner and outer loops. Our framework covers all the classical Wasserstein gradient flows including the heat equation and the porous medium equation. We demonstrate the performance and scalability of our algorithm with several numerical examples.

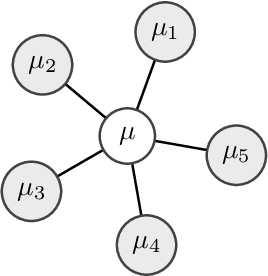
On the complexity of the optimal transport problem with graph-structured cost

Multi-marginal optimal transport (MOT) is a generalization of optimal transport to multiple marginals. Optimal transport has evolved into an important tool in many machine learning applications, and its multi-marginal extension opens up for addressing new challenges in the field of machine learning. However, the usage of MOT has been largely impeded by its computational complexity which scales exponentially in the number of marginals. Fortunately, in many applications, such as barycenter or interpolation problems, the cost function adheres to structures, which has recently been exploited for developing efficient computational methods. In this work we derive computational bounds for these methods. With $m$ marginal distributions supported on $n$ points, we provide a $ \mathcal{\tilde O}(d(G)m n^2\epsilon^{-2})$ bound for a $\epsilon$-accuracy when the problem is associated with a tree with diameter $d(G)$. For the special case of the Wasserstein barycenter problem, which corresponds to a star-shaped tree, our bound is in alignment with the existing complexity bound for it.

Scalable Computation of Monge Maps with General Costs

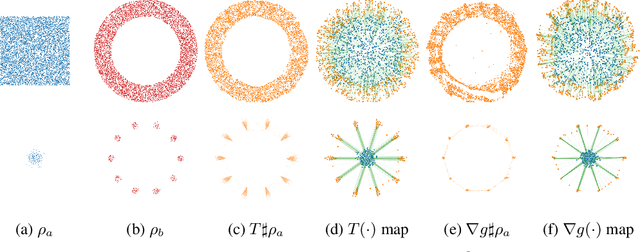
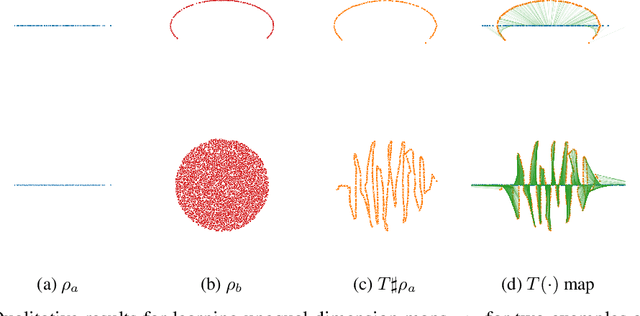
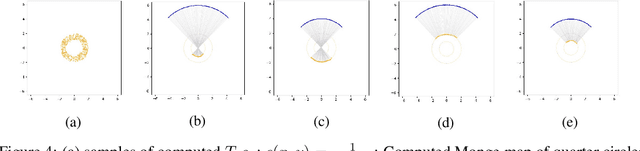
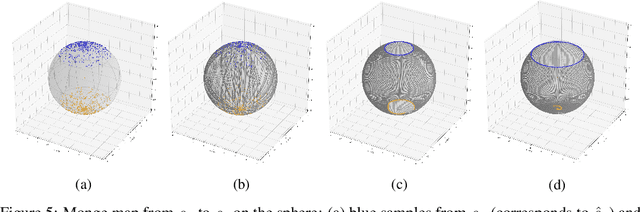
Monge map refers to the optimal transport map between two probability distributions and provides a principled approach to transform one distribution to another. In spite of the rapid developments of the numerical methods for optimal transport problems, computing the Monge maps remains challenging, especially for high dimensional problems. In this paper, we present a scalable algorithm for computing the Monge map between two probability distributions. Our algorithm is based on a weak form of the optimal transport problem, thus it only requires samples from the marginals instead of their analytic expressions, and can accommodate optimal transport between two distributions with different dimensions. Our algorithm is suitable for general cost functions, compared with other existing methods for estimating Monge maps using samples, which are usually for quadratic costs. The performance of our algorithms is demonstrated through a series of experiments with both synthetic and realistic data.