Scalable Computation of Monge Maps with General Costs

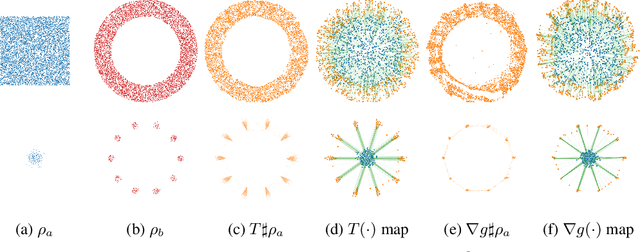
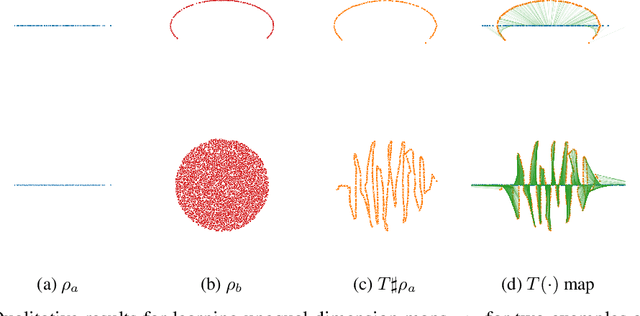
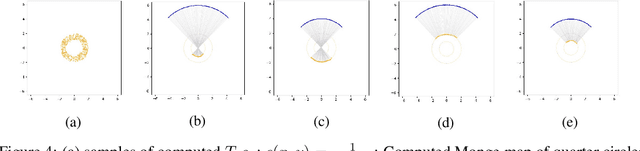
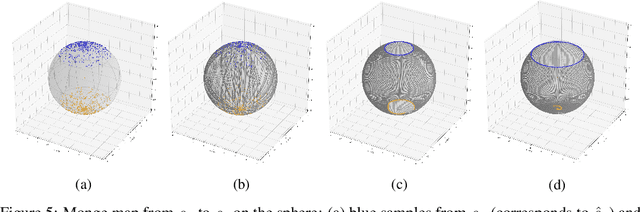
Monge map refers to the optimal transport map between two probability distributions and provides a principled approach to transform one distribution to another. In spite of the rapid developments of the numerical methods for optimal transport problems, computing the Monge maps remains challenging, especially for high dimensional problems. In this paper, we present a scalable algorithm for computing the Monge map between two probability distributions. Our algorithm is based on a weak form of the optimal transport problem, thus it only requires samples from the marginals instead of their analytic expressions, and can accommodate optimal transport between two distributions with different dimensions. Our algorithm is suitable for general cost functions, compared with other existing methods for estimating Monge maps using samples, which are usually for quadratic costs. The performance of our algorithms is demonstrated through a series of experiments with both synthetic and realistic data.

Mean Field Game GAN

We propose a novel mean field games (MFGs) based GAN(generative adversarial network) framework. To be specific, we utilize the Hopf formula in density space to rewrite MFGs as a primal-dual problem so that we are able to train the model via neural networks and samples. Our model is flexible due to the freedom of choosing various functionals within the Hopf formula. Moreover, our formulation mathematically avoids Lipschitz-1 constraint. The correctness and efficiency of our method are validated through several experiments.

Learning High Dimensional Wasserstein Geodesics

We propose a new formulation and learning strategy for computing the Wasserstein geodesic between two probability distributions in high dimensions. By applying the method of Lagrange multipliers to the dynamic formulation of the optimal transport (OT) problem, we derive a minimax problem whose saddle point is the Wasserstein geodesic. We then parametrize the functions by deep neural networks and design a sample based bidirectional learning algorithm for training. The trained networks enable sampling from the Wasserstein geodesic. As by-products, the algorithm also computes the Wasserstein distance and OT map between the marginal distributions. We demonstrate the performance of our algorithms through a series of experiments with both synthetic and realistic data.

Learning Stochastic Behaviour of Aggregate Data

Learning nonlinear dynamics of aggregate data is a challenging problem since the full trajectory of each individual is not observable, namely, the individual observed at one time point may not be observed at next time point. One class of existing work investigate such dynamics by requiring complete longitudinal individual-level trajectories. However, in most of the practical applications, the requirement is unrealistic due to technical limitations, experimental costs and/or privacy issues. The other one class of methods learn the dynamics by regarding aggregate behaviour as a stochastic process with/without hidden variable. The performances of such methods may be restricted due to complex dynamics, high dimensions and computation costs. In this paper, we propose a new weak form based framework to study the hidden dynamics of aggregate data via Wasserstein generative adversarial network(WGAN) and Fokker Planck Equation(FPE). Our model fall into the second class of methods with simple structure and computation. We demonstrate our approach in the context of a series of synthetic and real-world datasets.